在計算中提高思維能力
——《連方求和》教學實錄

文|裘陸勤

【教學內容】

適合各個版本的教材，屬于二年級上冊的數學拓展課。

【教學過程】

一、了解規則，認識連方

1.認識連方。

師：同學們，我們來認識一個新朋友——連方。每個數字寶寶都住在自己的小房間里，連方就是每個小房間的邊與邊要連在一起，不能是小房間的角落與角落連接，更不能是小房間之間跳了幾格的。（課件出示連方的正確情況和錯誤情況）

師：（課件出示二連方）像這樣3 和4 這兩個數字寶寶的小房間連在一起，就叫作二連方。你能找到其他二連方嗎？

生：4 和5。

生：10 和16。

2.尋找三連方。

師：同學們，三連方就是三個數字寶寶的小房間邊與邊連在一起，你能找到嗎？

生：2、3、4；3、9、15；1、2、7；4、9、10；……

3.判斷四連方。

師：剛才我們找到了很多三連方，老師這里有一些四連方，用你的火眼金睛判斷它們是不是四連方，說說你的理由。

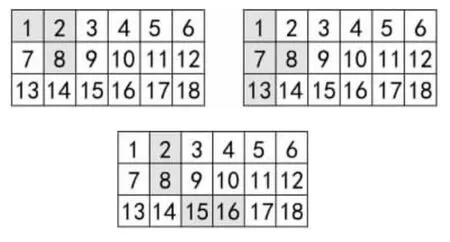
生：第1 幅不是四連方，因為只有三個小房間，四連方要有四個小房間；第2 幅是四連方，因為四個小房間的邊與邊連在一起；第3 幅不是四連方，因為有兩個小房間是角落和角落連在一起。

二、自主探究，有序思考

1.根據連續幾個數求和。

師：（課件出示三連方3、4、5）你會計算3＋4＋5 是多少嗎？

生1：3 加4 等于7，7 加5 等于12。

生2：我是用“移多補少”法，把5 給4 一個，它們都變成4 了，這里有3 個4，3×4=12。

師：（課件出示四連方1、2、3、4）你會計算1＋2＋3＋4 是多少嗎？

生1：1 加2 等于3，3 加3 等于6，6 加4 等于10。

生2：1 加4 等于5，2 加3 等于5，2×5=10。

生3：我先算1＋2＋3，把3 給1一個就都變成2 了，2×3=6，6＋4=10。

生4：我先算2＋3＋4，把4 給2一個就都變成3 了，3×3=9，9＋1=10。

師：你們都很棒，除了按順序依次計算，還可以用“頭尾搭配”或者“中間數×個數＋多余的數”來計算。

2.根據和推算連方中的數。

出示題目：連接下面方格里的數，使它們的和是30，用斜線涂一涂，并列出求和的算式。

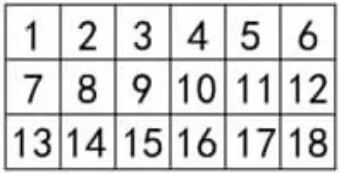
師：同學們，剛才題目告訴你連續幾個數讓你求和？現在告訴你和是多少讓你推算出連方中的數？先試著自己做一做，比一比誰想出的答案多。

師：老師看到大家找到了不少答案。現在我們試著從先確定數字個數的角度進行有序思考，想一想最少幾個數的和是30？

生1：兩個數，12＋18=30，因為沒有一個數是30。

師：你真會思考，老師就用你的名字來命名你的答案。（板書姓名）如果我們先確定三個數，要讓中間數最大，中間數會是多少呢？

生2：因為3×10=30，所以我去找中間數是10 的三個數。橫著看，我找到9＋10＋11=3×10=30；豎著看，我找到4＋10＋16=3×10=30。（板書學生姓名）

生3：我也是想3×10=30，然后去找三組和等于10 的算式：2＋8=10，3＋7=10，1＋9=10，而且1、2、3、7、8、9 這六個數是連在一起的。（板書學生姓名）

生4：我受到生3 的啟發，去找三組和等于10 的算式：1＋9=10，4＋6=10，2＋3＋5=10，而且1、2、3、4、5、6、9 這七個數是連在一起的。（板書學生姓名）

生5：我也是去找三組和等于10 的算式：2＋8=10，3＋7=10，1＋4＋5=10，而且1、2、3、4、5、7、8 這七個數是連在一起的。（板書學生姓名）

師：同學們，生2、生3、生4、生5 這幾種答案有沒有什么聯系和區別？

生6：相同點是他們都是根據乘法算式3×10=30 找到的。不同點是生2 是三個數的和等于30，生3、生4、生5 用的數比三個數多。生2 是用去找中間數寫算式，生3、生4、生5 都是去找三組和等于10 的算式。

三、學會遷移，總結提煉

1.在遷移中發現乘加。

師：同學們，我們思考了兩個數的和是30，中間數是10 的三個數和是30。我們先確定三個數，中間數除了10，還會是多少呢？

生1：剛才我們知道“中間數×個數＋多余的數”，我想到了3×9＋3=30。我就找中間數是9 的，橫著看，我找到8＋9＋10＋3=3×9＋3=30。（板書學生姓名）

生2：我也是找中間數9 的，我還把3 拆成了1 和2，所以8＋9＋10＋1＋2=3×9＋3=30。（板書學生姓名）

生3：我是豎著看的，中間數是9，3＋9＋15＋1＋2=3×9＋3=30。（板書學生姓名）

生4：我和他們都不一樣，我找到了加法算式15＋15=30，然后找到了三種不同的答案：（1）因為1＋14=15，7＋8=15，所以1＋14＋7＋8=30；（2）因為7＋8=15，2＋13=15，所以2＋7＋8＋13=30；（3）因為4＋11=15，5＋10=15，所以4＋5＋10＋11=30。（板書學生姓名）

師：我們根據同一個加法、乘法或乘加算式找到了多種不一樣的答案，還可以想到哪些算式呢？

生5：3 ×8 ＋6=30，3 ×7 ＋9=30，3×6＋12=30，3×5＋15=30，3×4＋18=30……

師：請你自己找一個乘加算式，先確定中間數，試著盡可能多的找出答案。

2.在總結中提煉方法。

師：同學們，剛才我們自主探究了“連方求和”，誰來總結一下是怎么解決“連方求和”問題的？

生：先根據和確定最少要幾個數，一般最少是兩個數；再考慮先確定三個數，根據“中間數×個數＋多余的數”寫出加法、乘法或乘加算式，圍繞中間數橫著看、豎著看找出符合條件的數。有時找到一種答案后，也可以考慮把一個數拆成幾個數。

四、全課小結，暢談收獲

師：同學們，這節課我們一起研究了“連方求和”，你有什么收獲呢？

生1：我在一開始找的過程中遇到了困難，我覺得不能放棄，可以換一種方法再試試。

生2：有序思考的方法可以找到很多符合要求的答案。

生3：學了今天這節課，我還想挑戰數字更多的連方。