一道高考模擬題的推廣及其證明
2022-12-26 09:15:32江西省修水縣第一中學332400冷清榮
中學數學研究(江西) 2022年12期
關鍵詞:拋物線
江西省修水縣第一中學 (332400) 冷清榮
圓錐曲線的定點定值問題是高考常考的一個熱點與難點問題,本文通過一道模擬題對其進行探究、類比及其推廣.
一、試題展示與解析

圖1
(1)求橢圓E的方程;
(2)若直線AM,AN與橢圓E的另一個交點分別為P,Q,記直線PQ,OH的斜率分別為k1,k2,判斷k1k2是否為定值?若是,求出這個定值;若不是,說明理由.
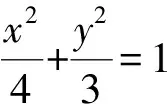
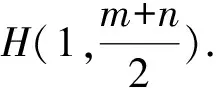
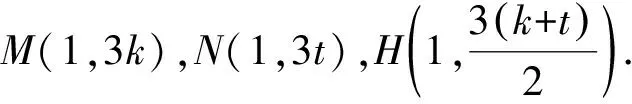
二、結論的推廣及其證明
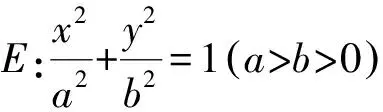
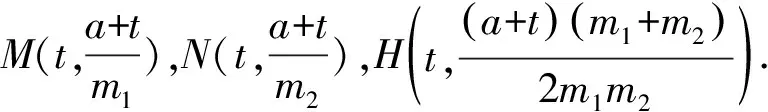
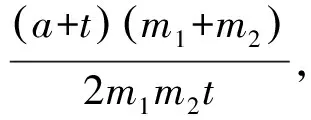
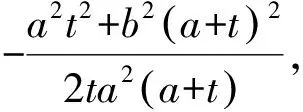
評注:本解法中沒利用韋達定理,而且也沒有完整求出P,Q兩點的橫坐標,計算更加直觀簡潔.
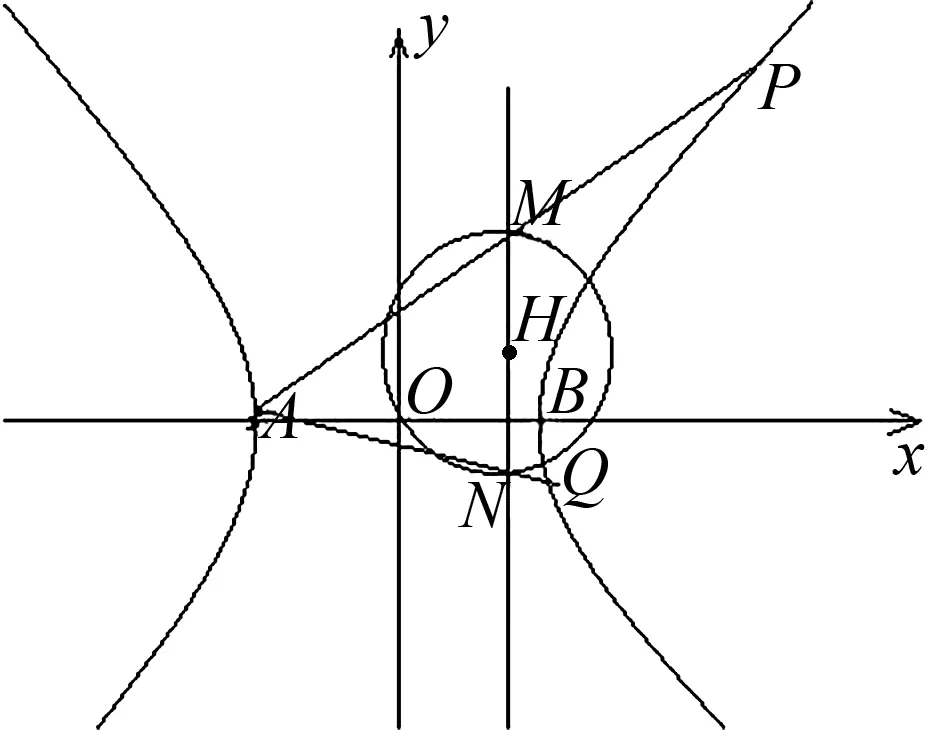
圖2
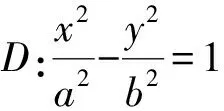
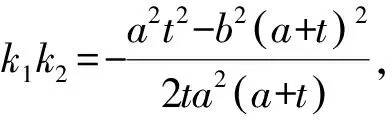
類似地,我們可進一步推廣到拋物線,得到一個美觀簡潔而且與直線l:x=t位置無關的結論.
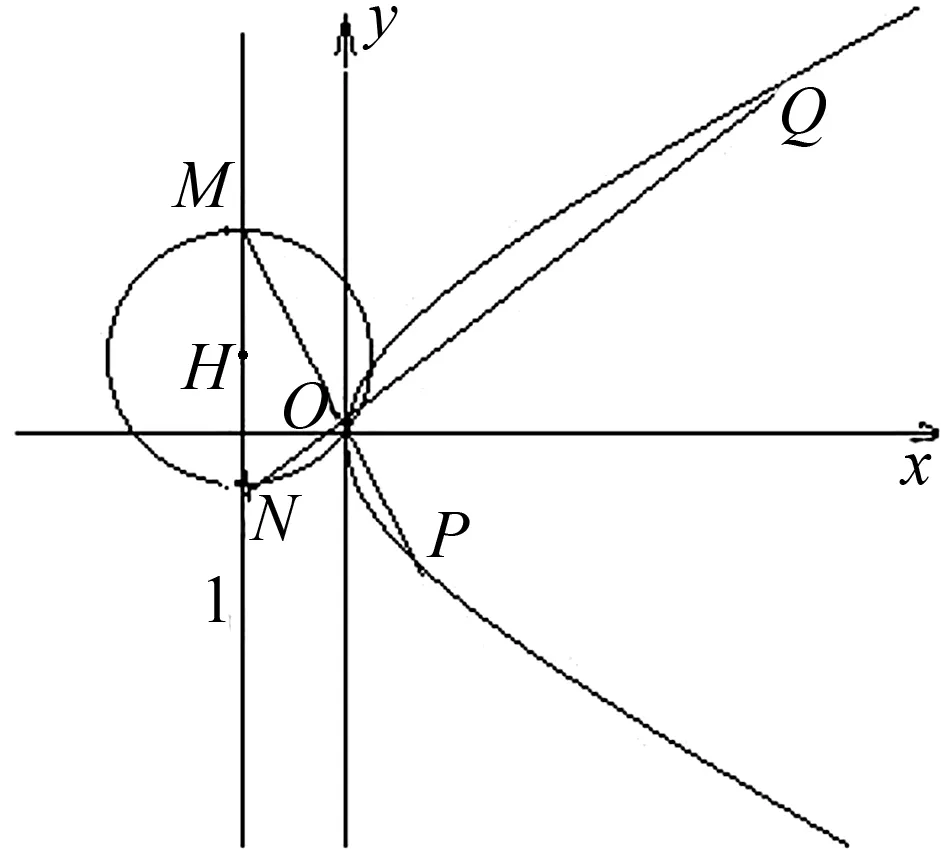
圖3
推廣3 如圖3,已知拋物線F:y2=2px,(p>0),點H是直線l:x=t上的動點,以點H為圓心且過原點的圓與直線l交于M,N兩點,若直線OM,ON與橢圓F的另一個交點分別為P,Q,記直線PQ,OH的斜率分別為k1,k2,判斷k1k2是否為定值?若是,求出這個定值;若不是,說明理由.
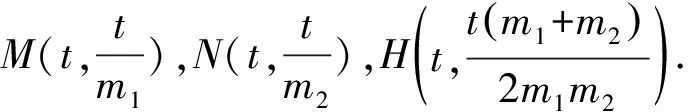
猜你喜歡
中學生數理化·高二版(2025年2期)2025-03-05 00:00:00
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:58
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:56
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
中學生數理化(高中版.高二數學)(2021年3期)2021-06-09 06:08:40
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:12
中學生數理化·中考版(2019年10期)2019-11-25 09:39:04
中學生數理化·中考版(2018年10期)2018-12-07 00:44:42
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38

