基于熵權法和TOPSIS方法的畢業要求達成度綜合評價方法

陳洪芳，高 毅，劉立霞

（北京工業大學，北京 100124）

在“雙一流”建設戰略新形勢、新使命下，工程教育專業認證以“學生為中心”“成果導向”“教育質量持續改進”為核心，對專業人才培養提出了更高要求。專業制定的畢業要求應能支撐培養目標的達成，因此，其應完全覆蓋工程教育認證通用標準中的12項畢業要求。畢業要求與高校、專業的培養目標相一致，是學生畢業時專業層面的學習培養成效的體現，同時也體現了專業在“知識—能力—素質”多維培養方面的教學效果。對不同屆畢業學生畢業要求達成度進行綜合評價，對于培養目標的修訂、持續改進具有重要意義，是檢驗工程專業人才培養是否滿足工程教育認證的12條通用標準要求的重要手段，是工程教育專業認證的核心內容之一。

按照信息論基本原理的解釋，信息是系統有序程度的一個度量，熵是系統無序程度的一個度量。根據信息熵的定義，對于某項指標，可以用熵值來判斷該指標的離散程度，信息熵值越大，已有的信息量就越小。相反，其信息熵值越小，指標的離散程度越大，該指標對綜合評價的影響（即權重）就越大。如果某項指標的數值全部相等，則該指標在綜合評價中不起作用。畢業要求中的每條都可以進行指標點的分解，利用信息熵這個工具，計算出各個畢業要求指標點的權重，可以為畢業要求的多指標綜合評價提供依據。

TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）方法屬于客觀賦權法，是解決多屬性決策的排序方法，更是有效的多指標評價方法[1-2]。其基本思想是通過對原始數據進行規范化處理，消除不同指標量綱的影響，并充分利用原始數據信息，對有限方案進行多目標評價，從而反映各方案之間的差距，對待選方案進行決策，以便客觀真實地反映實際情況。通過構造評價問題的正理想解和負理想解，即各指標的最優解和最劣解，計算每個方案到理想方案的相對貼近度，對方案進行排序，選出最優方案。只要在屬性空間定義適當的距離測度就可以計算備選方案與理想解的距離。當出現兩個備選方案與正理想解的距離相同的情況，為了區分這兩個方案的優劣，引入負理想解，并計算兩個方案與負理想解的距離，與正理想解距離相同但離負理想解遠的方案為最優方案[3-5]。

工程能力包括多項技術能力和非技術能力，同時，每項能力的評價數據具有顯著的多源異構（定性、定量、權重未知等）特征。為了科學解讀畢業要求能力達成度的綜合評價數據，科學評價學生工程能力培養質量，并將評價結果應用于指導特色培養方案設計和實踐，文章運用基于熵權法和TOPSIS方法的畢業要求達成度綜合評價方法，結合北京工業大學測控技術與儀器專業（以下簡稱測控專業）工程教育專業認證實踐，構建不同屆畢業學生畢業要求達成度評價模型，同時，基于不同屆畢業學生畢業要求達成度評價值，給出綜合評價結果，對不同屆畢業學生畢業要求達成情況進行排序，為多源異構評價數據的科學解讀提供依據。

一、基于熵權法的畢業要求指標點權重確定方法

以北京工業大學測控專業為例，分析畢業要求達成度評價相關數據，如何對12項畢業要求進行賦權是一個關鍵問題。僅依靠每項畢業要求給出的達成度評價值直接使用熵權法計算權重并不客觀，因為支撐每個指標的因素不一樣。因此，需要對每項畢業要求進行分析，找出能夠代表該指標的屬性。

測控專業畢業要求達成度評價以每門課程考核材料作為評價依據。首先，由二級單位教學指導委員會對課程考核方式進行合理評價。其次，對于課程考核方式評價為合理的課程，由二級單位教學指導委員會指定專人對課程（包括實踐教學在內的所有教學環節）達成畢業要求的情況進行評價。最后，二級單位教學指導委員會根據每門課程達成度評價結果，計算出畢業要求達成度評價結果并進行備案。測控專業的12項畢業要求均分解為若干畢業要求指標點，每條畢業要求指標點有3～5門課程作為支撐。

通過分析，每項畢業要求中具有重要影響作用的因素有：指標點個數、支撐該項畢業要求的教學活動課程數及支撐該項畢業要求的教學活動課程總學分數。因此，文章采用熵權法確定這3個屬性的權重，進而確定12項畢業要求的權重。

將第k屆畢業生12項畢業要求設置為待評方案，3個屬性分別是：指標點個數（Ti，1）、支撐該項畢業要求的教學活動課程數（Ti，2）和支撐該項畢業要求的教學活動課程總學分數（Ti，3）。首先，基于離差標準化法對12項畢業要求的屬性值進行規范化處理，使不同量綱的屬性可以進行比較。指標點個數歸一化計算公式如下。

支撐該項畢業要求的教學活動的課程數歸一化計算公式如下。

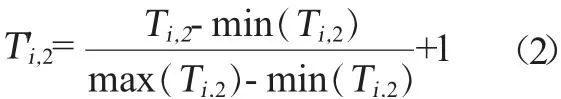
支撐該項畢業要求的教學活動課程總學分數歸一化計算公式如下。

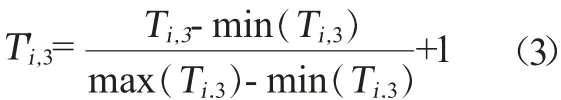
根據公式（1）至公式（3），可以計算出歸一化后的指標點個數、支撐該項畢業要求的教學活動課程數和支撐該項畢業要求的教學活動課程總學分數屬性值。

根據歸一化指標點個數的比重pi，1計算公式，計算每項畢業要求的不同屬性值占該屬性12項畢業要求總屬性值的比重，具體公式如下。

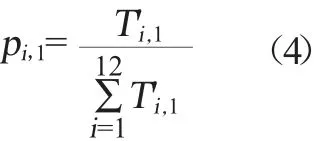
歸一化支撐該項畢業要求的教學活動課程數的比重pi，2計算公式如下。

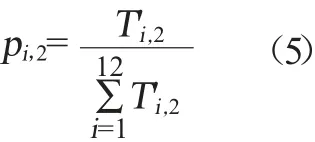
歸一化支撐該項畢業要求的教學活動課程總學分數的比重pi，3計算公式如下。

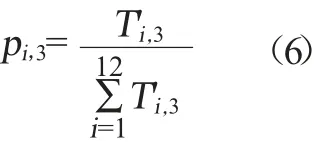
基于公式（4）至公式（6），可以得到指標點個數、支撐該項畢業要求的教學活動課程數和支撐該項畢業要求的教學活動課程總學分數屬性的比重結果。

其次，由于可以用熵值來判斷某個屬性的離散程度，即其信息熵值越小，屬性的離散程度越大，該屬性對該項畢業要求綜合評價的影響就越大。因此，需要計算12項畢業要求中每個屬性的熵值。

指標點屬性的信息熵值的計算公式如下。

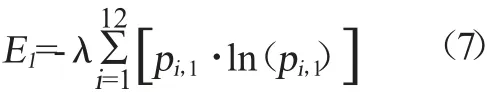
同樣可以得到支撐該項畢業要求的教學活動課程數屬性的信息熵值E2為0.98，支撐該項畢業要求的教學活動課程的總學分數屬性的信息熵值E3為0.97。

計算不同屬性信息熵冗余度dj=1-Ej（j=1，2，3），以此來表示不同屬性的信息效用值。指標點個數、支撐該項畢業要求的教學活動課程數和支撐該項畢業要求的教學活動課程總學分數3個屬性的信息效用值分別為0.01、0.02、0.03。

依據公式（8）計算每個屬性的權重，得出指標點個數、支撐該項畢業要求的教學活動課程數和支撐該項畢業要求的教學活動課程總學分數3個屬性的權重分別為0.32、0.33、0.35。具體公式如下。

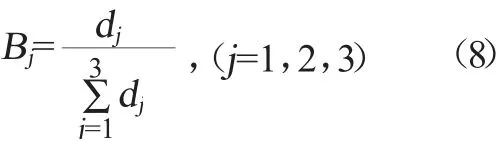
最后根據公式（9）計算每項畢業要求在整體方案評價中所占的權重Wi。具體公式如下。

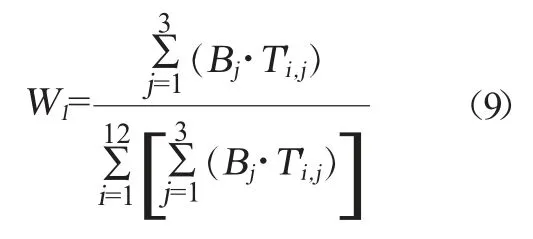
圖1為12項畢業要求的權重。從權重結果可以看出，畢業要求1和畢業要求10相對其他畢業要求更重要。

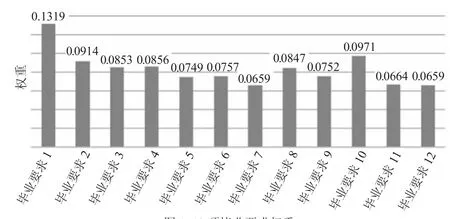
圖1 12項畢業要求權重

二、基于TOPSIS方法的不同屆畢業學生的畢業要求達成度綜合評價

文章以北京工業大學測控專業2017屆至2020屆畢業學生的畢業要求達成結果為例。Zi，k表示2017屆至2020屆畢業學生畢業要求達成情況,用i=1，2，3，…，12分別表示12項畢業要求，k=1，2，3，4分別表示2017屆至2020屆畢業學生。利用熵權法可以計算出每項畢業要求在整體方案評價中所占的權重Wi，因此可以直接利用線性加權方法，利用公式（10），確定加權的畢業要求達成度數據Ck，i。具體公式如下。

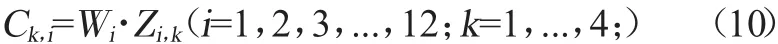
基于以上加權的畢業要求達成度數據，根據公式（11）可以確定12項畢業要求的正理想解C*i，根據公式（12）可以確定12項畢業要求的負理想解C-i。具體公式如下。

利用公式（13）和公式（14），采用加權的歐幾里得范數的方法，計算2017屆至2020屆畢業學生的畢業要求達成度到正理想解與負理想解的距離。具體公式如下。

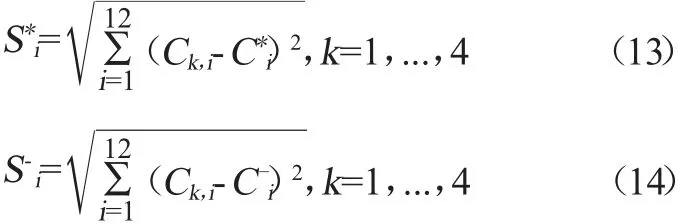
基于歐幾里得距離，根據公式（15）計算不同屆畢業學生的畢業要求達成度綜合評價fi結果。如果某一屆畢業學生的畢業要求達成度距離正理想解越近，距離負理想解越遠，則fi就越大，表明這一屆的畢業學生的畢業要求達成度就越好。具體公式如下。

經計算，北京工業大學測控專業2017屆至2020屆畢業學生的畢業要求達成度綜合評價結果分別為0.6379、0.4303、0.1808、0.7132。

文章成果應用于北京工業大學測控專業學生的工程能力培養，評價持續改進效果，指導持續改進方向，培養人才的工程能力得到穩步提升。自2013年起，北京工業大學測控專業以工程教育專業認證為契機，緊密圍繞培養“優秀工程人才”，不斷探索特色培養模式，深入體系化教學改革。2015年，北京工業大學測控專業成功通過了工程教育專業認證，2018年再次通過工程教育專業認證（有效期六年）。

測控專業畢業學生解決測控技術與儀器“復雜工程”問題的能力得到用人單位好評。測控專業學生對工程能力的自我需求也顯著提高，深造率逐年遞增，從2014年的15.80%上升至2020年的54.55%，2020年深造率高于學校平均水平7.68個百分點。其中，測控專業學生國內深造率從2014年的15.80%上升至2020年的25.45%，2020年國內深造率高于學校平均水平2.26個百分點；出國深造率從2014年的0上升至2020年的29.09%，2020年出國深造率高于學校平均水平5.4個百分點。

測控專業畢業學生獲得中國儀器儀表學會見習工程師資格比例從2014年的0上升至2020年的100%。專業影響力逐年提升，2020年報考第一志愿率高達53.5%。

文章通過熵權法獲得12項畢業要求的權重，所得結果表明，畢業要求1所占權重最大，12項畢業要求中畢業要求1的屬性影響因素最多。

采用TOPSIS方法構建不同屆畢業學生的畢業要求達成度評價模型，測評測控專業不同屆畢業學生的培養質量。研究結果表明，2020屆畢業學生的畢業要求達成度綜合評價值最高，2017屆、2018屆、2019屆依次降低。2020屆畢業學生的畢業要求達成度整體最優，2019屆畢業學生的畢業要求達成度整體相對較差。

文章提出基于熵權法和TOPSIS方法的畢業要求達成度綜合評價方法，利用信息熵計算各項工程能力支撐指標點的權重，采用TOPSIS方法（客觀賦權法）消除異構數據的量綱差異影響，為畢業要求能力達成度的綜合評價數據的科學解讀提供依據，同時評價結果應用于指導特色培養方案設計和實踐。