結構化材料,讓單元整體教學更具生命力
——以計數器在《除數是一位數的除法》教學中的應用為例
文|丁 偉
教學材料是學生學習思辨的對象,也是引發思辨的根本。材料的選取需要依據教學內容的特點和學生思維水平,助推學生思維走向深刻,引發高質量的學習。
人教版三年級下冊第二單元《除數是一位數的除法》是小學筆算除法的關鍵期和轉折期,前聯二年級下冊《有余數除法》(一層豎式),后延四年級下冊《除數是兩位數的筆算除法》(多層豎式),教學意義非常重要。
一、解讀現有材料對教學的影響
教材在“被除數是兩位數的除法”中呈現了小棒圖幫助學生理解算理,通過細化分小棒的步驟——先分“4 個十,再分2 個一”,凸顯了小棒圖對豎式過程中算理理解的重要性。而在“被除數是三位數的除法”中,教材只提供情境,不再呈現算理信息,沒有其他學習材料幫助體驗對算理的過程理解。沒有具體材料的支撐,則缺乏直觀的過程性體驗與理解,讓學習顯得抽象,學生的學習更多依靠前概念遷移。
二、不同素材價值對比——確定結構化材料
究竟怎樣的材料適宜整體性建構被除數是三位數的筆算除法?這就要求對于材料的選擇必須以數學知識為內核,能夠把零碎的數學知識和分散的教學環節串聯起來并貫穿于學習過程始終,體現出知識的內在邏輯性和系統性。由于被除數是三位數的筆算除法研究機理具有內在性的一脈相承,故筆者以256 表征為例從三個維度對比以下三種材料的價值,從而進行甄別與選取。
(一)能否更好體驗計數規則
不同材料情境下學生的思維活躍度是不一樣的。小棒表征是一根根小棒累加出來的,一根代表1,且形狀固定。人民幣表征1張可以代表1、10、100,而且形狀不同,故人民幣屬于實物直觀。計數器則用珠子表征,1 顆珠子可以代表1、10、100,而且珠子形狀相同。從抽象水平來看,小棒是最直觀的,人民幣次之,計數器最為抽象。小棒表征淡化了計數規則,人民幣本身自帶了大小的屬性,容易忽略對計數規則的關注,計數器在幫助學生體驗計數規則層面更具優勢。
(二)能否緊扣核心凸顯算理
小棒直觀易操作,當被除數是兩位數比較小的時候,通過操作能夠很好地將分的過程與除法豎式對接,助力算理理解。隨著被除數變大,繼續分小棒反而讓整個操作過程繁瑣。人民幣屬于實物直觀,從表面上看能夠適用于被除數是三位數的除法,但是由于材料本身自帶了大小屬性,對于算理的具體理解反而過于籠統了。計數器自身具有的位值原則和數位關系——當百位不夠分、結合十位繼續分;十位不夠分、結合個位繼續分。強化分物時先分什么、再分什么,結合分的過程體驗感悟除法豎式為什么是多層的原因。因此計數器適用范圍更具一般性且能凸顯除法運算的算理。
(三)能否體現知識內在原理一致性
表內除法(13÷4)和本單元起始課(42÷2、52÷2),教材都是用小棒圖表征,但是隨著被除數位數的增加,如(256÷2、256÷6)以及涉及到小數除法(22.4÷4),再用小棒、人民幣表征算理信息不僅麻煩而且困難。而計數器的引入,不管被除數是兩位數、三位數甚至小數,每次都是把除得的余數與低一位上的數合并繼續分,將思維聚焦在“計數單位轉換”這一核心,凸顯除法運算中余數不斷化成小單位繼續除的一般性道理。
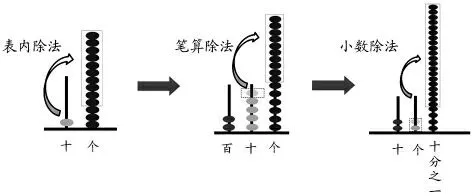
計數器因其能體現“退一當十”的計數規則,具有的位值原則使其在除法豎式計算中體現知識內在原理的一致性,所以計數器是合適的結構化教學材料。
三、發揮計數器價值——結構化材料貫穿單元整體教學
基于以上分析,以結構化材料計數器貫穿單元整體教學,以理解算理為核心,掌握算法為目標,通過適度調整教學路徑理解算理、有機整合教學內容溝通算理算法、重組教學板塊厘清思維混淆區,引導學生體驗知識原理的內在一致性,讓學生在本單元形成前聯后延的結構化思維與意識。
(一)適度調整教學路徑——計數器助力深度理解算理
教材的編排是先教學42÷2后教學52÷2,教學42÷2 時教材規定從高位算起,實際上42÷2 從低位算起是可以的(各個數位都能整除),此處教材的規定(從高位算起)與學生已有經驗、現實起點、認知邏輯都嚴重不符。
因此將“42÷2”和“52÷2”教學路徑互換,先教學“52÷2”后教學“42÷2”,多數學生由原先的順暢轉為糾結,因為無法直接得到結果,從而產生內在的探究欲望,減少負遷移影響。
【教學片斷】
環節一:任務驅動,診斷起點
出示任務:計算52÷2。

環節二:動手操作,理解算理
師:52 根小棒平均分成兩份,怎么分?
生:先分2 根,再分4 捆,最后拆開1 捆,分3 次得到26 根。
生:先分4 捆,再拆開1 捆和2 根合起來成為12 根。
師:兩種分法,哪里不同?
生:一種分了2 次,另一種分了3 次。
師:同樣平均分成兩份,為什么可以少分一次?
生:第二種分法把剩下的1捆和余下的2 根合起來一起分,所以少分了1 次。
師:小棒大家會分了,要是計數器上怎么體現剛才分的過程?
生:道理是一樣的,就是先分十位的5 顆珠子,剩下的1 顆珠子和個位合起來繼續分。
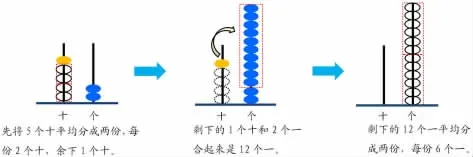
環節三:抽象概括,深化算理
計數器的適時引入引發學生不得不思考:剩下的一顆珠子怎么辦?由于計數器自身的位值原則,學生“退一當十”的思考一直伴隨在整個分材料的過程,從而將思維有效激活,助力深度理解算理。
(二)有機整合教學內容——計數器架起理法溝通橋梁
例3(256÷2)和例4(256÷6)兩節課結構相似,內容相近,有機整合教學內容更符合編排邏輯,用結構性材料不僅可以串聯整體認知,同時可以有效架起算理算法溝通橋梁。
【教學片斷】
環節一:任務驅動,診斷起點
出示任務:計算256÷2
環節二:動手操作,直觀理解
師:在計數器上分一分,結合分的過程,思考豎式過程的含義。
環節三:圖式對照,程序理解
環節四:語義表征,抽象理解
(1)結合圖式,你能說一說256÷2 的筆算方法嗎?
(2)還有256÷6,你覺得需要像剛才這樣教一遍嗎?為什么?
(3)現在你能說說被除數是三位數的筆算除法的方法嗎?
通過結構化的材料——計數器(半直觀半抽象)支撐起被除數是三位數的算理,讓操作環節直觀化、讓思維過程可視化,通過溝通直觀理解(動手操作)、程序理解(圖式對照)、抽象理解(語義表征)之間的關系和聯系,為抽象的算式尋找到具象的解釋,實現理法相融,不僅將整個操作過程“先分什么、再分什么、最后分什么”清晰呈現,同時凸顯對計數單位的關注。
(三)重組教學板塊——計數器厘清思維混淆區
人教版教材的編排是例6“208÷2”和“216÷2”、例7“650÷5”和“245÷8 分為”兩節課,但是這兩節課都包含著“除0 商0”“不夠商1 就商0”,學生在兩個知識點之間不停地切換。相比人教版,北師大版本的編排是將知識點是“除0商0”為一節(“306÷3”和“840÷6”),知識點是“不夠商1 就商0”為一節(“912÷3”和“522÷4”)。從學生的思維習慣而言,北師大版本的編排路徑更符合學情。
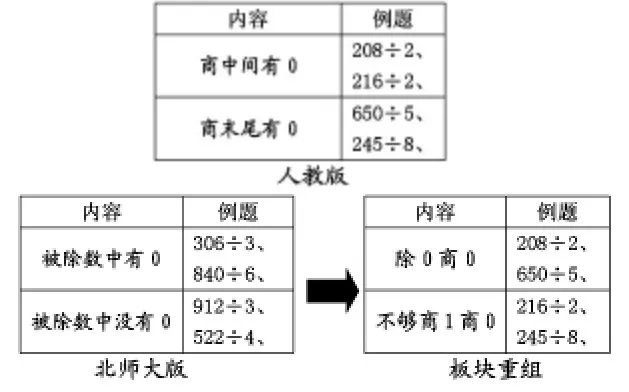
在此基礎上借助結構性材料計數器進一步幫助學生厘清思維混淆點。引導學生將“分——換——再分”這個過程與除法豎式有效融合,不僅讓學生直觀理解當大的計數單位不夠分轉化為更小的計數單位繼續分,同時直觀感知“除0 商0”“不夠商1 就商0”。
四、結構化材料對單元整體教學的啟示
(一)結構化材料如何選取
結構化材料的選取必須以數學核心知識為內核,能夠把零碎的知識和分散的教學環節串聯起來,體現出數學知識體系的系統性和內在原理的一致性。
(二)結構化材料使用策略
1.整體呈現,培養系統性思維
整體性呈現問題,將問題置于比較情境之中,學生對數學問題主動辨析、比較,體會知識之間的聯系,從而將相關知識點主動納入原有的認知結構中。
2.多元表征,滲透遷移性思維
計算教學中,算理是對算法的解釋,是理解算法的前提。算理理解越到位,算法建立越深刻。結構化材料計數器(半直觀半抽象)支撐起被除數是三位數的算理,讓操作環節直觀化、讓思維過程可視化,通過溝通直觀理解(動手操作)、程序理解(圖式對照)、抽象理解(語義表征)之間的關系和聯系,為抽象的算式尋找到具象的解釋,實現理法相融。

