初中解方程問題的障礙分析與對策探索

武言好

【摘 要】解方程問題是初中階段數學知識體系中的一大重點內容，初中學生在解方程問題中容易遇到各種障礙。文章從各類型方程的典型題目著手，在具體解題實踐中分析中學生解方程問題過程中的障礙及成因，探究學生主要解題障礙類型，并提出相應的教學建議，以期為一線教師提供參考。

【關鍵詞】初中數學 解方程 障礙分析 改進策略

【中圖分類號】G623.5? ? 【文獻標識碼】A? 【文章編號】1002-3275（2023）10-42-05

方程問題是初中數學問題的關鍵類型之一，數學考試十分重視考查學生解決方程問題的能力。部分初中學生不擅長解決方程類的問題，認為這一內容的學習十分困難，在解方程問題過程中經常遇到各種障礙。影響中學生掌握解方程方法的原因復雜多樣，如教師教授時問題講解不透徹、訓練不夠等，學生對概念不理解、存在思維定式等。通過分析解方程案例，發現學生在解題過程中所遇到的障礙，并提出合理解決方案，更有助于教師把握問題所在，從而幫助學生突破障礙，提高學習質量。

一、初中解方程問題障礙分析研究的必要性

（一）數學學習解題障礙問題的研究受到較多關注

數學是一門高度抽象、邏輯嚴密、應用廣泛的學科，學生在數學學習中常常會遇到障礙。國外對數學解題障礙的研究要追溯到20世紀。“在1925年，Buswell、Judd兩位學者基于已有的30多項研究對學生的算術錯誤進行了一次診斷分析。緊隨其后，德國和蘇聯等國家也相繼開展了學生算術錯誤的有關研究。后來，由于教學實際的需要，對數學解題錯誤的有關研究不再局限于計算錯誤，而是不斷將范圍擴大到代數、幾何等領域。”［1］在這種情況下，障礙歸因分析的重點從數學知識本身開始轉移到學習心理方面。20世紀80年代，國內就有學者對中學學生數學解題障礙進行了研究，在分析數學解題錯誤成因時，從數學學科知識體系角度去考慮，并逐漸涉及教育學和心理學方面。［2］

（二）解方程是初中階段非常重要的學習內容

解方程問題屬于應用數學問題的一部分，而應用數學問題是培養學生理解數學應用的有效工具，也是反映學生基本技能發展的重要手段。在數學教學領域，教師常教導學生使用方程、不等式和函數來解決問題，這樣有助于學生形成相應的解題應用模式并加深對方程的理解，從而促進學生數學基本技能的發展，符合核心素養的培養要求。此外，涉及方程的應用問題也是初中數學的重點內容。

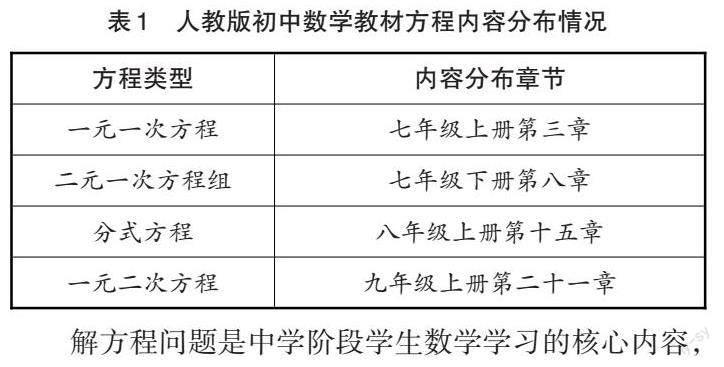
例如人教版七年級上冊和下冊、八年級上冊、九年級上冊數學教材都有大量關于解方程問題的章節，具體分布情況如表1所示。

解方程問題是中學階段學生數學學習的核心內容，也是對教師教學具有挑戰性的部分。

（三）關于解方程障礙問題的研究相對較少

通過文獻檢索發現，關于方程的研究很多，但大多集中于比較教材或習題、教學設計、教學策略上，而以解方程問題的障礙作為依據的研究相對較少，只有少數研究分析特定類型的方程或不等式解題錯誤。筆者通過對實際教學中的方程問題進行舉例分析，列出初中教材與方程問題有關的章節，分別對一元一次方程、二元一次方程組、分式方程和一元二次方程的典型題目進行分析，根據具體的題目來分析學生在解方程問題中所遇到的障礙，并就此分析障礙成因，研究解決對策，從而提出相應的教學建議，以期幫助教師解決教學難題。

二、初中學生解方程問題的主要障礙表現

（一）數學概念模糊

在數學解題過程中，部分學生對題目相關的基本概念性質存在理解不清、掌握不到位的問題，或是不恰當地運用與題目毫無關系的其他數學概念，從而使解題過程產生障礙，無法順利得出正確答案。上述問題在一元一次方程、二元一次方程組、分式方程、一元二次方程等解題過程中都有所體現，現以一元二次方程問題為例說明。

例題：將下列方程化成一元二次方程的一般形式，并寫出其中的二次項系數、一次項系數和常數項。

障礙分析：一元二次方程是等號兩邊都是整式，只含有一個未知數，且未知數的最高次數是2的方程，其一般形式是[ax2+bx+c=0a≠0]。其中，[ax2]是二次項，a是二次項系數；[bx]是一次項，b是一次項系數；c是常數項。如果學生未能很好地掌握一元二次方程的概念及其一般形式，就很難作答上述方程概念類問題，不知以何種形式寫出一元二次方程的一般形式，也很難指出一元二次方程的二次項系數、一次項系數等，甚至連項的系數都無法理解。

在教學實踐中發現，有概念性質類做題障礙的學生，大多無法在課堂上集中注意力聽講，容易出現概念性質理解錯誤，或者課后未能夠及時地進行學習鞏固，從而對概念理解不全面，產生做題障礙。

（二）運算錯誤

部分學生對運算法則掌握不牢，不清楚運算的數值，混淆運算的過程規則，從而出現運算錯誤。

學生按照規范的解題步驟運算，這樣的解題格式簡潔美觀，思路清晰，不容易造成計算結果錯誤。

另外，教師還需強調在解二元一次方程時注意“代入消元法”和“加減消元法”過程中的符號變化，解分式方程和一元二次方程時，注意檢驗最后的計算結果是否符合題意。同時在平時的運算練習過程中，教師要提醒學生注意運算順序，先乘除后加減，有括號先算括號里的數。注意運算過程中不要漏寫、抄錯數字，以及注意計算結果中小數點的位數是否正確，這樣一來就能有效減少由運算障礙導致的解題錯誤。

（三）注重解題步驟，化繁為簡

這一障礙主要是針對一題多解的情況，一題多解的題目往往較復雜，且包含較多等量關系，學生解這類題時應嚴格按照解方程問題的一般步驟進行。中學階段解方程問題的一般步驟包括7個，如圖1所示。

教師應在解題指導課以及平時的課堂解題演示中，嚴格遵循解題一般步驟，引導學生養成良好習慣，讓學生能輕松地將數量關系轉化為方程表達式，從而便于學生找到最優解題方法。

（四）合理把控審題速度，抓取關鍵詞

學生在審題時應學會通過抓取關鍵詞來尋找解題思路和方法，可以用筆將關鍵詞勾畫出來，再聯系生活實際去理解題目。在課堂上，教師引導學生閱讀題目時要合理把控速度，不能一味追求解題速度，并通過個人示范和實例有效地引導學生。如果學生在讀完題目后仍然很糾結，可以引導他們關注實際生活中與之相關的問題，找到相應條件，再回到問題本身，解決問題。此外，教師還可以嘗試開展情境化教學，即創設與學生生活實際貼近的情境，讓學生在情境中解方程，理解更抽象的含義。在這個過程中，學生可以從自己的生活中找到參照物，將抽象的概念形象化，充分理解問題的含義。

例如“一個圓的面積是[2πm2]，求它的直徑”，教師需要引導學生在審題過程中抓取關鍵詞“求直徑”。長此以往，引導學生形成抓取關鍵信息審題的習慣，更好地把握題目的數量關系和降低審題的難度，從而順利地解題。

（五）鼓勵啟發學生，引導學生保持積極的解題情緒

教師在教學中要以啟發和鼓勵教育為導向，幫助對做題有心理障礙的學生走出困境。例如在課堂上開展解題互動，發現學生的解題障礙，適時為學生提供支架，引導學生思考，并向學生仔細講解解題方法，鼓勵學生嘗試運用正確方法解題，這樣能有效緩解學生的畏難情緒。同時讓學生在解題中發現運用數學知識的樂趣，從而調動學生的積極情緒，提升學生的解題能力。此外，教師需要長期關注學生的解題情緒，改進教學方法，對解題心理障礙較嚴重的學生，可以遞進式地引導其消除心理障礙，日積月累，讓他們真正成為學習的主人。

本文以教材中的方程題目為案例，呈現初中學生解方程問題時障礙的具體表現，并對其進行成因分析，提出相應的改進策略。希望本文中的一些策略和方法能為教師的實際教學提供參考。

【參考文獻】

［1］李蓉．初中生“方程與不等式”解題中的錯誤分析及對策研究：以甘肅省慶城縣兩所中學為例［D］．蘭州：西北師范大學，2020：7.

［2］同［1］8.