心內科臨床實習教學中引入循證醫學思想的應用探討
蔣伏平,陳霓紅.南京醫科大學附屬南京醫院老年科,江蘇南京 0006;.南京醫科大學附屬南京醫院神經內科,江蘇南京 0006
心內科臨床實習教學中引入循證醫學思想的應用探討
蔣伏平1,陳霓紅2
1.南京醫科大學附屬南京醫院老年科,江蘇南京210006;2.南京醫科大學附屬南京醫院神經內科,江蘇南京210006
目的探究心內科臨床實習教學中引入循證醫學思想的應用方法及其效果。方法對該院2008年9月—2010 年9月間80名心血管內科臨床實習生進行實習教學,將80名學生按照隨機序號法分為觀察組和對照組;對照組采用常規實習教學方法進行教學,觀察組在對照組基礎上引入循證醫學思想進行教學;觀察兩組教學結果并進行對比。結果 觀察組學生實踐部分和理論部分得分均高于對照組,同時觀察組對于該教學的滿意率95%高于對照組75%,兩組比較P<0.05,差異有統計學意義。結論心內科臨床實習教學中引入循證醫學思想的效果良好,提高學生對于相關知識的掌握效果,并且能夠明顯提高學生對于教學的滿意率,因而值得在實習教學過程中推廣使用。
心內科;臨床實習教學;循證醫學思想;效果
[Abstract]Objective To study the application method and effect of the introduction of evidence-based medicine idea in the clinical practice teaching in the department of cardiology.Methods 80 clinical practice students in the department of cardiovascular medicine from September 2008 to September 2010 in our hospital were randomly divided into two groups,the control group adopted conventional practice teaching method for teaching,the observation group adopted the evidencebased medicine idea for teaching on the basis of the control group,and the teaching results of the two groups were observed and compared.Results The practice scores and theoretical scores in the observation group were higher than those in the control group,meanwhile,the satisfactory rate of teaching in the observation group was higher than that in the control group (95%vs 75%),and there were obvious differences between the two groups by comparison with statistical significance,P<0.05.Conclusion The effect of the introduction of evidence-based medicine idea in the clinical practice teaching in the department of cardiology is good,which can improve the student's mastery effect of relevant knowledge and obviously improve the student's satisfactory rate of teaching,therefore,it is worth promotion and application in the course of practice teaching.
[Key words]Department of cardiology;Clinical practice aching;Evidence-based medicine idea;Effect
心內科是我國臨床上較早使用循證醫學的學科,也是在診療中循證醫學證據較完備的學科。因此實習生在臨床實習的過程中,單純地學習理論知識已滿足不了將來臨床的需求[1],循證醫學已經滲透到心內科知識的方方面面;在臨床實習的過程當中,常規的實習教學就是對實習生進行知識的傳授,并且按照教學大綱進行相關知識的講解,雖然當堂教學的效果較好,但學生對于知識的掌握不夠到位,很難真正調動實習生的自我管理能力和主動學習的興趣,因此常常出現教學效果不佳的情況[2];有研究表明,對實習生進行心內科實習教學的過程中引入循證醫學思想,能夠提高教學的效果。因而該研究對該院2008年9月—2010年9月間80名心內科臨床實習生進行隨機分組實習教學,分組后對照組采用常規實習教學方法進行教學,觀察組在對照組基礎上引入循證醫學思想進行教學對比效果,現報道如下。
1 資料與方法
1.1一般資料
對該院2009年1月—2010年12月間80名心內科臨床實習生進行按照隨機數字法分為觀察組和對照組;每組各40名,對照組中男16名,女24名,年齡22.5~26.0歲,平均年齡(24.12±1.01)歲,平均學分(3.65± 0.93);觀察組中男17名,女23名,年齡23.0~26.5歲,平均年齡(24.15±1.05)歲,平均學分(3.68±0.97);兩組實習生的年齡、性別、平均學分等一般資料差異無統計學意義,P>0.05,具有可比性。
1.2方法
對照組采用常規實習教學方法進行教學,即由帶教的實習指導老師按照教學大綱對實習生進行常規的知識傳授,并且按照教學大綱中常規的查房練習,同時對經典案例進行分析和學習[3];觀察組在對照組基礎上引入循證醫學思想進行教學,即結合常規的教學方法,告知學生按照相關疾病的病因、機制、臨床表現和相關成功的循證醫學治療方案進行結合[4];引導學生提出相關問題,查閱大量資料,結合理論知識,提出有嚴格循證醫學證據的個體化治療方案,通過有力的循證醫學證據,進一步理解各種病因、發病機理在該疾病發生發展中的不同作用和重要性,并比較各種藥物的多種藥理作用在該疾病治療中的利弊,在問題的基礎上對病例進行分析,并進行相關知識的歸納[5],理解最優化治療組合方案的來由。在學習過程中加強學生查閱文獻,融會貫通,分析和解決問題的能力。教學結束后,觀察兩組教學結果并進行對比。
1.3觀察指標
對實習生的基本情況進行觀察,同時采用理論知識考核和實踐考核對學生進行評價,理論知識的試題均從該院題庫中隨機選取,內容均為心內科臨床的相關知識,由實習生現場作答,由指導老師進行考卷的閱覽和評分;實踐考核包括文獻查閱、病案分析和診療方案方面的內容。兩部分滿分均為100分[6],分數越高表示教學效果越好;另對兩組關于該教學的滿意率進行調查,將問卷設置為很滿意、較滿意和不滿意三項,令實習生進行勾選,總滿意率=(很滿意數+較滿意數)/總數x100%[7],將兩組所得數據進行統計和分析。
1.4統計方法
2 結果
2.1兩組理論部分得分比較
觀察組理論知識得分高于對照組,兩組比較P<0.05,差異具有統計學意義。詳見表1。2.2兩組實踐部分得分比較

表1 兩組理論部分得分比較
觀察組實踐部分得分高于對照組,兩組比較存在明顯差異,P<0.05,差異有統計學意義。詳見表2。
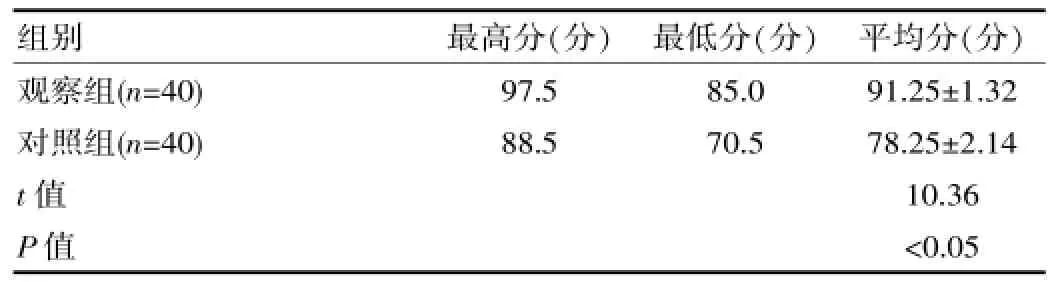
表2 兩組實踐部分得分比較
2.3兩組滿意率比較
觀察組對于該教學的滿意率95%高于對照組75%,兩組比較存在明顯差異,P<0.05,差異有統計學意義。詳見表3。
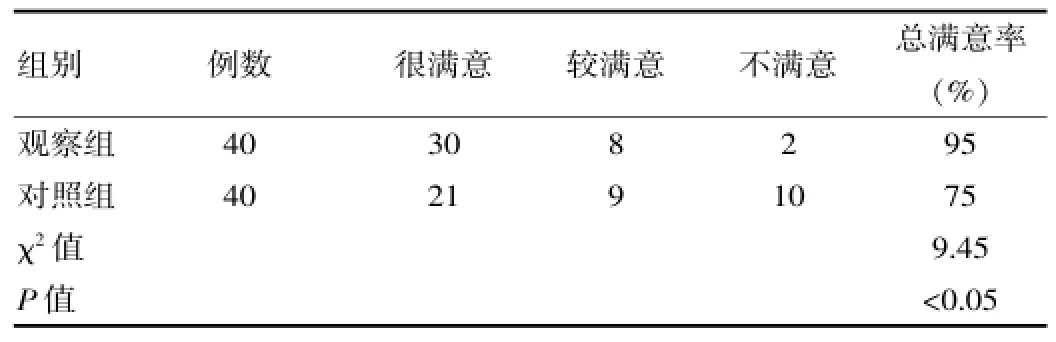
表3 兩組滿意率比較
3 討論
循證醫學屬于一種系統的醫學模式,即在臨床中遵循有力證據,獲得問題解決的方法;隨著近年來我國經濟技術的不斷發展和進步,醫學教育的模式和方向也不斷得到突破,旨在培養更多適合時代發展腳步的新型人才[9];與此同時,循證醫學也得到了迅猛的發展,在醫學學科的教育中也得到了越來越多的應用。醫學學科學生在進行學習的過程中,基本會接觸到全面的理論和基本知識,待到學生以實習生的身份踏入實習單位,臨床實習就成為增長知識和鞏固基礎的重點所在,其中包括學生對于所學基本知識的應用,還包括臨床相關技能的學習,并且對學生踏入崗位進行一個初步的引導[10];因此實習教學也就成為關鍵問題,同時如何對學生進行良好的實習教學就成為我們共同關注的問題。常規的教學是對學生需要掌握的知識進行基本的講解,同時由帶教老師進行傳授,而學生在當堂基本感覺掌握得相關的知識,在需要運用時發現大多掌握的不夠扎實,直接影響學生對于工作的效率和效果,因而在常規的教學方法上運用有效的方法進行彌補,也成為一個重要問題。
在當前的心內科臨床實習教學過程中,所采用的教學模式還是主要以傳統的教學模式為主,在開展教學的過程中,重視學生對臨床知識及臨床經驗的積累,尤其是要求學生對于所掌握知識的連貫性與完整性,這種主動灌輸的教學模式,雖然能夠提升學生的知識量,但是學生的臨床實際診療能力往往比較差,而且不利于其自主學習能力的培養。引入循證醫學思想的教學模式作為一種新型的教學模式,其整個教學模式可以概括為:提出問題-尋找證據-分級評價證據-應用證據,整個教學的過程中,是以臨床問題為中心的,其通過引導學生對大量文獻資料進行查找、總結,能夠從中找出最新的、最好的解決相關問題的依據,并且在教師的引導之下,能夠完成對相關解決途徑的實用性與真實性的嚴格評價,并且能夠結合醫院真實的病例進行判斷,分析,在這種教學模式中,不僅有利于學生知識量的增長,另一方面,學生在查找問題、分析問題、解決問題的過程中,整個過程全程參與,能夠有效提升主動學習能力,并且這一過程的學習也有利于其樹立起正確的醫學觀。而循證醫學證據在心血管內科診療中的大量積累,使心內科臨床實習教學中應用循證醫學思想的教學方法成為切實可行的教學方法。
該研究中觀察組學生理論部分和實踐部分得分均高于對照組,同時觀察組對于該教學的滿意率95%高于對照組75%,兩組比較差異具有統計學意義。反映了學生在整個學習的過程中,由被動接受變為主動學習,其文獻檢索資料查閱、分析總結問題等各方面的能力都得到了有效的鍛煉和提升,更有利于其在步入到工作崗位之后,實際診療能力的有效提升,這也可以看出,與傳統的教學模式相比,引入循證醫學的教學模式是更有利于學生整體發展的一種教學模式,同時學生也更為認可。
綜上所述,心內科臨床實習教學中引入循證醫學思想的效果良好,提高了學生對于相關知識的掌握效果,并且能夠明顯提高學生對于教學的滿意率,因而值得在實習教學過程中推廣使用。
[1]王兵,客蕊,陳會君.循證醫學理論在內科臨床實習中的應用[J].中國中醫藥現代遠程教育,2014,12(4):87-88.
[2]王學惠,劉善庭.心臟內科臨床實習生培養策略[J].現代醫藥衛生,2016,32(4):945-947.
[3]李幼平,李靜,孫鑫,等.循證醫學在中國的發展:回顧與展望[J].蘭州大學學報:醫學版,2016,42(1):25-28.
[4]葉樂平,湛美正,李園,等.PBL教學模式聯合循證醫學在兒科呼吸教學查房中的應用探索[J].新課程研究(中旬刊),2015,(6):69-71.
[5]珠勒皮亞·司馬義,陳玉嵐,陳曦.心血管病循證醫學教學模式初探[J].繼續醫學教育,2012,26(12):16-19.
[6]盧玲,李愛民,藺亞東.CBS教學法對中醫臨床帶教老師教學能力的影響[J].中國衛生產業,2015(35):117-119.
[7]饒玉梅.微信在婦科臨床教學中應用初探[J].中國繼續醫學教育,2016,8(4):15-17.
[8]穆清爽,張繼云,劉海英.CBL聯合PBL教學法在呼吸臨床教學中的應用探索[J].繼續醫學教育,2016,30(3):30-31.
[9]羅秋育,林揆斌.循證醫學模式在腫瘤內科臨床實踐教育中的應用[J].繼續醫學教育,2016,30(3):19-20.
[10]郭威,王秀清,王明濤,等.多種教學模式和方法在臨床內科教學中的應用[J].中國繼續醫學教育,2016,8(6):3-4.
[11]吳少賢.循證醫學思想在呼吸科臨床實習生帶教中的應用[J].醫療裝備,2015,28(12):107-108.
[12]高素萍,劉杏菊.在婦產科教學中實施循證醫學教育初探[J].衛生職業教育,2009,27(16):88-89.
[13]李建華,張力燕,汪矗,等.基于導學式教學法與循證醫學PICOS模式相結合方式在臨床教學中的可行性分析[J].西北醫學教育,2014,22(1):173-176.
Application Study on the Introduction of Evidence-based Medicine Idea in the Clinical Practice Teaching in the Department of Cardiology
JIANG Fu-ping1,CHEN Ni-hong2
1.Geriatric Department,Affiliated Nanjing Hospital of Nanjing Medical University,Nanjing,Jiangsu Province,210006 China;2.Department of Neurology,Affiliated Nanjing Hospital of Nanjing Medical University,Nanjing,Jiangsu Province,210006 China
R19
A
1672-5654(2016)04(c)-0126-03
10.16659/j.cnki.1672-5654.2016.12.126
蔣伏平(1975.7-),男,江蘇無錫人,主治醫師,研究方向:心血管內科。
陳霓紅(1978.3-),女,江蘇鹽城人,研究生,主治醫師,研究方向:神經內科臨床,E-mail:neon_2000@163.com。
2016-01-24)

