“拋物線”跨學科融合教學的探索與實踐

銅梁中學校 (402560) 莫紹會

1 跨學科融合教學的必要性

1.1 時代發展的需要

當今世界,科學技術的發展水平不僅代表著一個國家的經濟實力,更展現了一個國家的綜合國力,但任何科技成果都不是單獨某一個學科的成就,它一定是多個學科成果的融會貫通,這就需要融合多門學科知識,構建全面認知以解決問題. 數學作為科技發展的理論基礎,為各行各業的發展做出了極大貢獻,數學教學需要盡早培養學生的跨學科應用意識,結合高中學生的認知規律,逐漸滲透數學的跨學科交互運用意識,教師更應當勇于破除既往的學科限制,努力地完善學生的學習觀念.

1.2 課程改革的需要

《普通高中數學課程標準(2017 版)》指出:“數學是自然科學的重要基礎,并且在社會科學中發揮越來越大的作用,數學的應用已滲透到現代社會及人們日常生活的各個方面……高中數學課程強調數學與生活以及其他學科的聯系,提升學生應用數學解決實際問題的能力”[1]. 高中課程改革是學生發展核心素養的需要,核心素養強調學生發展的全面性和整體性,注重挖掘知識背后隱藏的學科能力、學科思維方法,關注對真實問題的分析和解決. 而我們面臨的大多數問題具有綜合性,依靠單門學科的知識不足以解決,這就需要突破學科限制,跨學科融合教學便成為改革的必然趨勢.

1.3 學生發展的需要

在現實生活中,跨專業的“復合型”人才更受親耐. 為適應社會發展和個人終生發展,學生要成為“全面發展的人”,要發展核心素養,需要具備跨學科能力,從多學科視角認知和思考現實問題,運用相關學科知識解決現實問題. 高中數學跨學科融合教學能開拓學生的視野,增加跨學科應用的體驗,培養學生的數學學習興趣,拓展學生的數學應用意識,提升學生的數學核心素養, 進一步培養和提高學生的合作能力、理解能力、實踐能力和創新能力.

1.4 教師發展的需要

新高考、新教材、新課標對高中數學教師提出了更高的要求,作為高中數學教師,必須及時學習,更新觀念,逐漸具備全面的跨學科領域教學的知識, 需要教師從“專才”變為“通才”,才能適應學生的發展,跟上改革的步伐. 因此,教師在提升本學科教學素養的同時, 也應涉獵其他學科的知識,至少是與本學科內容相關的知識,這樣才能融會貫通地進行跨學科知識能力整合提升的教學,有效提升教師的專業水平,促進教師自身的發展.

本文以人教版普通高中教科書選擇性必修一3.3“拋物線”為例,談談如何具體實施跨學科融合教學.

2 “拋物線”跨學科融合教學的實踐

2.1 融合信息技術打造高效課堂

傳統的黑板加粉筆的教學早已不適應現在的課堂了,隨著科學技術的進步,各種新興技術融入到了教學當中,尤其現代高中數學課堂,已經與PPT、幾何畫板、Geogebra 等信息技術深度融合,讓數學課堂由抽象變直觀,由靜態變動態,由枯燥變生動,有了信息技術的加持,教師可以輕松打造有趣、高效、可視化的數學課堂. 在“拋物線”一節中,融合信息技術的優勢體現得淋漓盡致. 例如在這節伊始(如圖1),教材就利用幾何畫板作圖演示拋物線的形成過程,要求學生根據作圖過程,觀察、思考、發現動點滿足的幾何特征,進而分析、歸納提煉出拋物線的定義,正是有幾何畫板作圖在先,學生才容易發現規律,輕松突破認知障礙. 本節中,信息技術的使用當然不只這一處,下文將陸續展示信息技術已經深度融合到各個教學環節之中.

圖1

2.2 融合物理學科探尋性質本源

數學與物理的關系十分密切,大多數物理學家都精通數學,例如發現三大運動定律和萬有引力定律的物理學家牛頓也是偉大的數學家,還有笛卡爾、拉格朗日等等,每一次物理學的重大革命, 其標志都是有新的數學被引入到物理中來,牛頓就是在研究瞬時速度等物理問題時發明了微積分,可見,在數學教學過程中不可避免會經常與物理打交道,只有充分利用與物理學科的融合進行教學,才能讓學生切實體會到現實世界的物理規律可以用邏輯嚴密的數學原理來解釋.

教學片段1拋物運動的軌跡是拋物線

師: 為什么要學習拋物線?

生1: 是自然界物體運動的普遍規律.

師: 是的,請看小視頻(視頻中有踢足球,打籃球,噴水池噴出的水柱, 美麗的煙花等場景), 踢足球時足球飛出的弧線、打籃球時籃球拋出的弧線、噴水池噴出的水柱的運動軌跡、煙花爆炸時運動的軌跡等等都是拋物線.

師: 為什么拋物運動軌跡就是拋物線呢? (思索一會兒教師引導)我們不妨以斜上拋運動為例,讓小球P從O點開始作斜上拋運動,v0為拋出速度,θ為v0與水平方向夾角,g為重力加速度,t為時間,求小球運動的軌跡方程(給學生兩分鐘時間獨立思考,再兩分鐘時間小組合作探究)

生2: 以O為坐標原點, 以水平方向為x軸建立直角坐標系(如圖2 所示) , 設小球P的坐標為(x,y), 則x= (v0cosθ)t,,消去t, 得到小球運動的軌跡方程這是一個二次函數,因為二次函數的圖像是拋物線,所以小球的運動軌跡是拋物線.

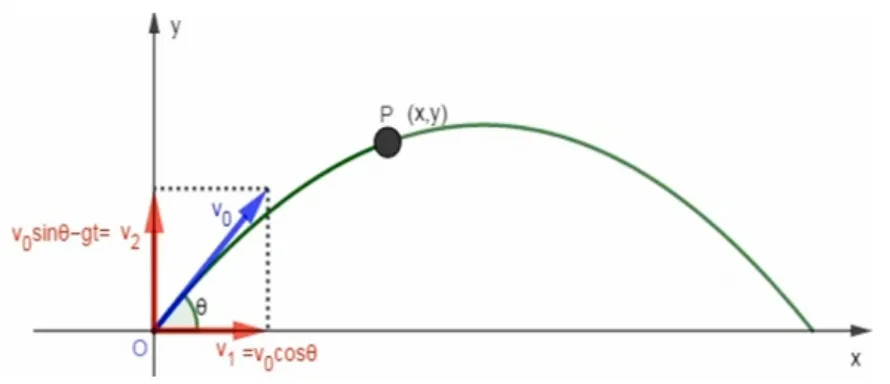
圖2

師: 很好,你的做法與伽利略是一致的,17 世紀就是伽利略證明了拋體運動軌跡是拋物線.

設計意圖用小視頻的方式吸引學生的注意力,增加學習的樂趣,培養學習數學的興趣,更直觀的讓同學們體會到拋物線在現實生活中無處不在,培養學生用數學眼光觀察世界,進一步加深“數學來源于生活”的認識. 順勢拋出問題,引發同學們思考,激發學習的欲望,探尋自然現象的原理,融合數學與物理學科的知識解決問題,培養學生數學建模、邏輯推理、數學運算的核心素養,進一步加深“數學是自然科學的基礎”的認識,感悟數學的科學價值. 配合Geogebra 動態呈現,給學生親眼所見的真實感,同時還可以培養直觀想象的核心素養.

教學片段2拋物線的光學性質

師: 拋物線的光學性質是指什么?

生1: 從拋物線焦點發出的光線,經拋物線反射后,反射光線平行于拋物線的對稱軸;同樣,平行于拋物線的對稱軸的光線,經拋物線反射后,反射光線過焦點.

師: 拋物線為什么會有這樣的性質? (給學生兩分鐘時間獨立思考,再兩分鐘時間小組合作探究,老師適時給與點撥引導,學生完成證明)

生2: 如圖3 所示,設拋物線的標準方程為y2=2px(p＞0), 焦點,x軸上方的函數解析式為設P(x0,y0) 為其上任意一點, 可求得過P點的切線l方程為y0y=p(x+x0), 過P點作該切線的垂線m方程為py+y0x=py0+x0y0,m與x軸交于點A(x0+p,0), 則所以|AF| = |PF|,所以α=β,過P作x軸的平行線PB,則θ=β,所以α=θ,同理可證拋物線的下半部分也滿足. 所以拋物線有前面所述的光學性質.

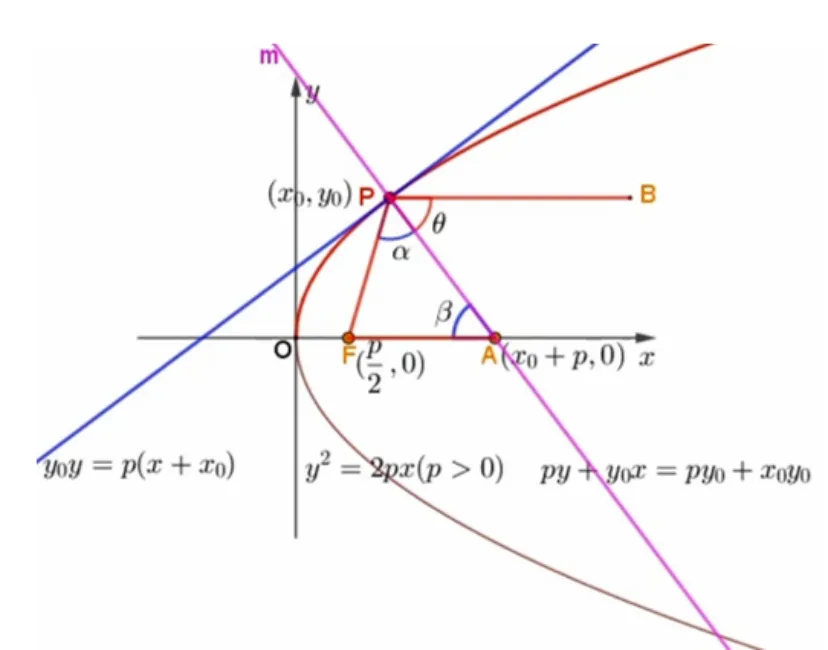
圖3

2.3 融合科技生活感受強大應用

教學片段3拋物線在生活中的應用

師: 拋物線有“聚光”的性質,人們在生產生活中是如何利用這種性質的?

生1: 手電筒、探照燈、太陽照等等(學生說不全面,老師播放一個自制小視頻補充說明)

師: 很好,如視頻所示,還有某些橋梁的設計、射電望遠鏡、中國天眼、拋物線麥克風等. 中國天眼是國之重器,是祖國的驕傲,它是目前世界上工作能力最強的射電望遠鏡,能夠實現實時300 米口徑的拋物面功能,請同學們課后查閱資料,了解中國天眼背后的故事.

設計意圖用小視頻的方式更直觀的讓同學們體會到人們是如何利用拋物線的,進一步加深“數學來源于生活,又用于生活”的認識,感悟數學強大的應用價值和科學價值,同時培養學生的愛國熱情和民族自豪感. 天眼的首席科學家兼總工程師南仁東就是一個跨學科型全才的實例,天文學、力學、機械工程、巖土工程等樣樣精通,而且他身上執著的科研精神和愛國精神也是同學們學習的榜樣.

2.4 融合建筑藝術體現審美情趣

教學片段4“拋物線在建筑中的應用”

師: 建筑師在設計時融入拋物線,既考慮拋物線的物理性質,又帶給人們美的享受. 請看圖片,回答問題(播放PPT,展現各種橋梁、隧道的圖片).

師: 我國著名的趙州橋的橋拱是拋物線嗎? 金門大橋的形狀是拋物線嗎? 杰斐遜紀念拱門的形狀是拋物線嗎? 彩虹的形狀是拋物線嗎? (學生不能完全回答,故留作課后思考.讓學生帶著問題來上課,又帶著新的問題下課).

設計意圖面對生活中各種各樣的曲線,要思考什么是拋物線什么不是拋物線? 探尋未知,查閱資料,獲得新知,多角度、跨學科思考問題,培養學生觀察、質疑、釋疑的能力,培養學生發現和提出問題、分析和解決問題的能力,即培養學生“四能”,培養學生綜合能力和創新能力,同時培養學生“會用數學眼光觀察世界,會用數學思維思考世界,會用數學語言表達世界”.

2.5 融合數學史實體驗千年艱辛

教學片段5拋物線的發展歷程

師: 大家知道拋物線為什么叫拋物線嗎?

生1: 因為是拋物運動的軌跡,所以取名拋物線吧.

師: 是的,我們中文就是根據這個規律命名的,但要回答這個問題,需要了解拋物線的發展歷程,請看視頻.

教師播放自制微課視頻,大致內容為: 古希臘梅內克繆斯是最早系統地研究圓錐曲線的數學家,他用垂直于圓錐一條母線的平面來割圓錐,圓錐的軸截面是等腰三角形,當頂角為銳角、鈍角、直角時得到三條不同的曲線,分別將它們命名為銳角圓錐曲線、鈍角圓錐曲線、直角圓錐曲線(均為古希臘語,這三條曲線就是今天的橢圓、雙曲線、拋物線,當時雙曲線只發現一支)[2]. 后來古希臘另一數學家阿波羅尼斯全面研究了圓錐曲線并寫成巨著“圓錐曲線”,他是第一個用同一個圓錐的截面來研究圓錐曲線的人,也是第一個發現雙曲線有兩支的人,因研究方法不同,根據研究過程將三種曲線命名為“虧曲線、超曲線、齊曲線”(也為古希臘語),取代了之前梅內克繆斯的命名,后來英語翻譯寫為: ellipse,hyperbola,parabola[3]. 中文早期有人將它們翻譯成“虧曲線、超曲線、齊曲線”,與阿波羅尼斯研究過程的原始含義很接近. 今天中文教科書里的橢圓、雙曲線是根據形狀命名,拋物線則是根據物理學的拋物運動軌跡命名. 以前人們都是用純幾何的方法研究圓錐曲線的,直到17 世紀,笛卡爾創立了坐標系,人們對圓錐曲線的認識才進入了一個新階段.

設計意圖追溯歷史起源,感悟數學的文化價值,讓學生體會任何科學發展都會經歷一個長期艱難的過程,由一代又一代科學家奉獻畢生精力積累而成的,鼓勵同學們熱愛科學,為科學發展做出自己的貢獻!

3 反思總結

網上流傳著這樣的調侃:“科學的盡頭是數學”,雖有一些夸張,但也表明了大眾對數學的認識: 數學是一門基礎性、工具性、綜合性、應用性很強的學科. 數學的發展歷程也表明,數學與各個學科聯系密切,數學是一門很古老的學科,很多學科都是從數學中分離出來的. 教師在教學過程中應多注重與其它學科的融合,讓學生切身感受到數學是有趣的,數學是有用的,數學是無處不在的,數學是邏輯嚴密的. 就比如圓錐曲線,從古至今人們沒有停止過對它的學習研究,一方面是因為人們對數學問題的癡迷,另一方面也是人們探索天體運動、自然規律的樸素渴求. 總之,通過跨學科融合的教學,可以開拓學生的視野,激發學生學習數學的熱情,增強學生學習數學的自豪感,可以培養學生的數學應用意識,提升學生的數學核心素養.