放手學生發(fā)問，打造數(shù)學“問學”課堂

冒昌梅

“問學”課堂是以“問”為主，倡導學生自主發(fā)問，教師要聚焦學生的“問題”，以“問”為主線，引導學生從問題探究中，去生疑，去解惑，去獲智。數(shù)學學科的抽象性、邏輯性的特點，導致很多學生不會問。“問學”課堂的構建，始于學生的先學后問，由問而學，最終達成以“問”促學、以“問”促教的目標。子曰：“敏而好學，不恥下問。”在數(shù)學課堂上，教師要鼓勵學生發(fā)問，讓學生主動地參與課堂學習，搭建平等、輕松、快樂的數(shù)學課堂。

一、明確學生主體地位，啟發(fā)學生提問

在數(shù)學“問學”課堂，教師要尊重學生的主體地位，為學生創(chuàng)設自主發(fā)問的環(huán)境。

（一）貼近學生生活，激發(fā)學生發(fā)問的欲望

數(shù)學與生活密不可分，在初中數(shù)學課堂，圍繞一些數(shù)學知識點，教師可以搭建生活化情境，由學生去認識、去發(fā)現(xiàn)，激發(fā)學生發(fā)問的欲望。

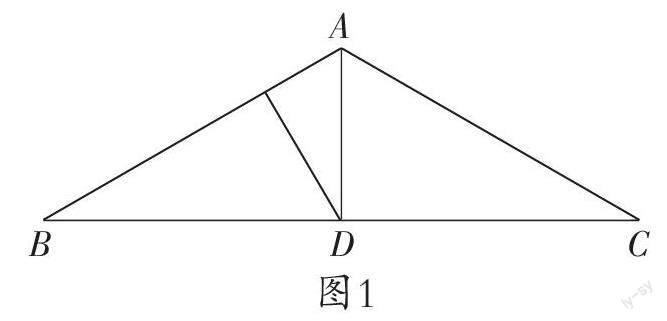
比如，在學習“等腰三角形”時，圍繞等腰三角形的特點、性質以及邊與角的關系，教師出示一些民居圖片。觀察這些圖片，讓學生想一想，提出問題。有學生提出這些特色民居的屋頂很有趣，結構就是一個等腰三角形。教師根據(jù)學生的發(fā)現(xiàn)，在黑板上將屋頂結構畫成圖1所示的等腰三角形。

學生的好奇心被激發(fā)，順勢對該等腰三角形進行描述，已知AB=AC，立柱AD⊥BC，BC=6，∠BA C=120°，問∠B是多少度，AD的長度是多少？接下來，利用等腰三角形的性質，分別得到腰所對應的角相等，再根據(jù)頂角、垂直關系，得到∠B為30°。根據(jù)等腰三角形“三線合一”定理，進而算出AD的長度為√3。

由此，從具體聯(lián)系到抽象，再由抽象轉換到具體，讓學生對等腰三角形的知識點有了深刻的理解。

（二）抓住學生疑問，引導學生深度思考

“問學”課堂，要鼓勵學生大膽質疑。正所謂，學貴有疑，教師要轉變觀念，將課堂交給學生，指導學生去提問。學生有了問題，才能更好地深入思考，才能提高數(shù)學課堂學習效率。

比如，在學習“余角和補角”時，一些學生對何為“余角”，何為“補角”總是不明白。教師出示一張由兩堵墻圍成的院角，并挑選一位學生，讓其站在院子外面，問如何求出其“余角”和“補角”。該學生提出質疑：僅僅給出一個角，是不能求出該角的余角和補角。這時，引導學生對比兩個概念，“互為余角”與“互為補角”，請同學思考余角和補角的特點。有學生發(fā)現(xiàn)，“互為余角”，說明這兩個角的和為“直角”即90°；“互為補角”，說明這兩個角的和為“平角”即180°。我們再對此進行具體化，∠A+∠B=90°，則∠A與∠B互為余角；同樣，∠A +∠B=180°，則∠A與∠B互為補角。順著這個思路，當測算出院子兩堵墻的夾角后，其余角、補角也能夠計算出來。

由此，從“互余”“互補”的概念出發(fā)，引領學生挖掘其特征，進而激發(fā)學生探究“余角”“補角”的能動性。學生在質疑、思辨中，進一步明晰“余角”“補角”的內涵。

（三）點撥學生方法，突破學習難點

在“問學”課堂，教師不僅要“教”，還要指導學生去“學”，掌握數(shù)學方法。教師要做到“讓學”，即引發(fā)學生主動去探究，助力學生開闊數(shù)學思維。學生懂得了“怎么做”，才能自主去探索、突破學習中的難點。

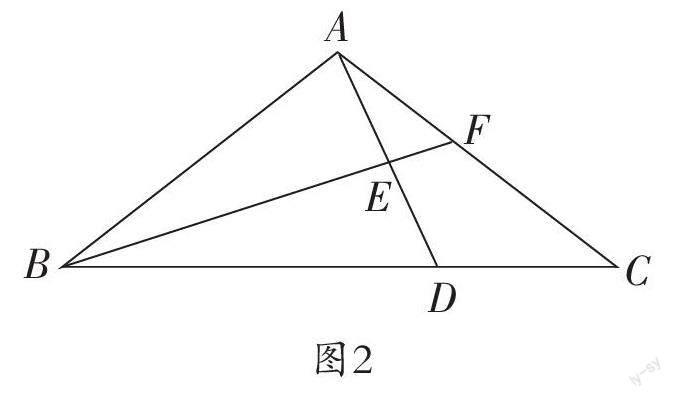
比如，在學習“相似判定和性質”時，認識“相似形”“相似比”，掌握“相似三角形的性質”，都是教學重點，也是學生普遍認為不好學的難點。如圖2所示。

已知△ABC，點D位于BC上，BD：DC=2：1，點E為AD的中點，BE交AC于點F。求BE：EF的值。觀察圖2，請學生思考并提出問題。有學生提問，既然要求解兩條線段的比值，則必須要證明兩個三角形相似，但找不到應該是哪兩個三角形。教師順勢點撥，求解BE與EF的比值，觀察BE和EF分別有哪些三角形與之相連。有學生找到了BE相連的三角形有△ABE、△EBD，EF相連的三角形只有△AEF。有學生提問，找出與△AEF似的三角形，就能找到對應關系。顯然，學生的視點都集中在△AEF上，教師再次點撥，一種是通過構造法，來構造一個與△AEF相似的三角形。怎么構造？有學生很快想到，過點D作BF的平行線，可以圍成“A”字形。根據(jù)4 E=ED，BD： DC=2：1，得到解法。另一種是，通過點D作AC的平行線，得到構造圖形，B、C、F三點構成“A”字形，進而求解出結果。

由此，順著學生的“發(fā)問”，教師要做好點撥、引領和啟發(fā)，幫助學生由“問題”中來，再到“問題”中去，鍛煉學生掌握數(shù)學思維方法。

二、把脈學生思維，從師生互動中揭示問題本質

“問學”課堂中，教師不是課堂包辦者，而是要將思考、探究賦權給學生，引領學生敢問、善問，提高學生學習力。教師要根據(jù)學生思維特點，調控好課堂“發(fā)問”進程，強調師生互動，構建參與性、發(fā)散性、開放性數(shù)學課堂。

（一）引出“問題串”，為學生搭建思維的階梯

“問題串”是一系列問題的連續(xù)性發(fā)問。教師在構建“問學”課堂時，要善于挖掘數(shù)學知識點之間的內在聯(lián)系，通過“問題串”引領，幫助學生循著“臺階”，學懂數(shù)學。

比如，某題中，京滬鐵路全長1462 km，貨車車速為o km/h，客車車速是貨車的2倍。問題：貨車從北京到上海，需要多長時間；貨車從北京到上海，比客車多用多長時間。對于這兩個問題，教師引導學生列出方程來描述兩者的數(shù)量關系。分析該題，主要考查學生對“分式”的認識和應用。在該題求解過程中，我們設置“問題串”如下：嘗試寫出客車速度的代數(shù)式？該題的解法，與之前哪種運算類似？討論分數(shù)通分、約分的依據(jù)？對分數(shù)與分式性質展開類比？方程中有分母，應該怎么處理？去分母后，該方程轉化為什么方程？據(jù)此，學生可以回顧所學的知識點，深入感受“分數(shù)”與“分式”的差異，再通過去分母，讓學生將“分數(shù)”“一元一次方程”等知識點串接起來。

學生借助于“問題串”的引領，從課堂上增強了自主思考、自主發(fā)問的意識，加深了對數(shù)學的理解和感悟。

（二）巧用類比思想，培養(yǎng)學生數(shù)學邏輯能力

數(shù)學思維能力的培養(yǎng)，需要漸進達成。在“問學”課堂上，教師要多運用類比思想，啟發(fā)學生去發(fā)現(xiàn)和提出問題，讓課堂提問更活躍。

由此，運用類比思想，讓學生體會到數(shù)學問題中的一般性與特殊性。運用類比思想，還可以拓展到分數(shù)與分式教學的比較，如一次函數(shù)與二次函數(shù)、反比例函數(shù)等之間的比較，從而促進學生數(shù)學邏輯能力的發(fā)展。

（三）強調動手實踐，洞明數(shù)學本質

“問學”課堂，學生由“問”而學，教師因學促“問”，師生之間要相互協(xié)作，助推學生進行深度學習。數(shù)學知識相對抽象，但數(shù)學是嚴謹?shù)膶W科，鼓勵學生動手“做”數(shù)學，在體驗中了解數(shù)學的本質。

比如，在學習“相交線與平行線”時，導人環(huán)節(jié)設置思考問題：在一個平面內，任意兩條直線之間，有怎樣的關系？有學生在紙面上畫出兩條直線，發(fā)現(xiàn)要么平行，要么相交。當教師提出“平行線是兩條直線之間的一種特殊關系”時，某學生舉手提出了質疑。該學生將手中的白紙舉起，并將兩邊進行重疊，原本平行的兩邊，這時卻“交”在了一起。該學生理直氣壯地闡述，很多學生也都表示了“認同”。教師并不要急于解釋，而是鼓勵學生去討論，去動手找出實例來推翻對方的觀點。最后，我們將“在一個平面內”作為條件，讓學生深刻體會到“平行線”定理描述的嚴謹性。

總之，數(shù)學課堂要引導學生去發(fā)問，去主動提出問題，進行獨立思考。在“問學”課堂上，教師要抓住“問”的契機，給予點撥、啟發(fā)和引導，讓學生從“問”中體悟數(shù)學學科之妙。