“雙根”技巧簡化運算,等價轉化探究本質
廣東省佛山市順德區容山中學 (528303) 黃桃榮
解決軌跡問題的一般方法是設點,通過題干發現點所滿足的關系式,化簡關系式求得結論.當題干條件復雜時,如何選擇切入點則是解決此類問題的關鍵.筆者研究了2023屆廣州市高三調研測試第21題,通過該題的解答過程,很好地體現了如何設點以及消元的完整過程,現將筆者的思考展現如下,以饗讀者.
一、題目
已知拋物線C:y2=2px(p>0)的焦點到準線的距離為2,圓M與y軸相切,且圓心M與拋物線C的焦點重合.(1)求拋物線C和圓M的方程;(2)設P(x0,y0)(x0≠2)為圓M外一點,過點P作圓M的兩條切線,分別交拋物線C于兩個不同的交點A(x1,y1)、B(x2,y2)和Q(x3,y3)、R(x4,y4),且y1y2y3y4=16.求證:點P在一條定曲線上.
分析:本題的主題干對拋物線與圓的信息交代的非常清晰,且考查的方式也很直接,拋物線C的方程為y2=4x,圓M的方程為(x-1)2+y2=1,過程略.本題的難點主要集中在第(2)問,涉及到了圓的切線,直線與拋物線相交,四個交點的縱坐標滿足某種關系式.并證明點P在一條定曲線上.考查的因素很多,且條件環環相扣,但所求的是一條軌跡問題.但題干沒有直接計算點P的軌跡(通過后文可知其軌跡為圓的一部分),該設問方式反而降低了要求(回避了分析在所求的軌跡中排除不滿足的部分).
二、解法呈現
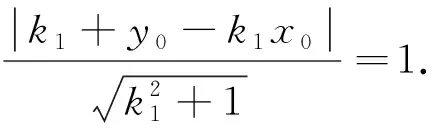
綜上即可知點P在定曲線x2+y2=1上運動.
評注:上述解法即是按照題干條件出現的順序,逐漸深入完成求解.思維過程簡單,但涉及到的運算量較大.但在本文中多次出現了“整體代換”的技巧,例如本文研究了k1的表達式后通過類比即可得k2的表達式,從y1y2到y3y4也是運用的該思想.
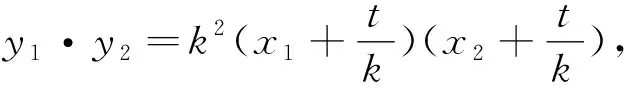
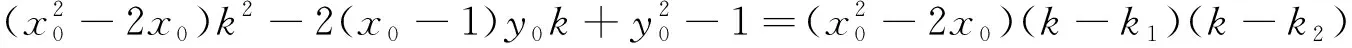
提示:若以m1,m2為變量,可直接設直線AB的方程為x=m1(y-y0)+x0進行運算.
三、背景探究及模型推廣
根據上面的解答過程可知,解題的核心在于對y1y2y3y4=16的解析,為了有效地說明該結論對應的本質.我們先看如下的一個引理.
引理設點P(t,0),過點P作直線l與拋物線C:y2=2px交于A(x1,y1)、B(x2,y2)兩點,則y1y2=-2pt.
證明:設直線l:x=my+t與拋物線的方程y2=2px聯立可得y2-2pmy-2pt=0.根據韋達定理可得y1y2=-2pt.
在原問題中,設直線AB,QR與x軸交點的橫坐標分別為t1,t2.根據引理可得y1y2=-4t1,y3y4=-4t2,即等價于t1·t2=1.那么原問題可進行如下的改述:設P(x0,y0)(x0≠2)為圓M:(x-1)2+y2=1外一點,過點P作圓M的兩條切線,設兩條切線與x軸交點的橫坐標分別為t1,t2,若t1·t2=1,求證:點P在一條定曲線上.
該轉述完全回避了拋物線的作用,回到了問題的本質.接下來,本文將嘗試直接轉述后的問題.

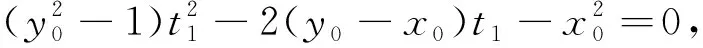
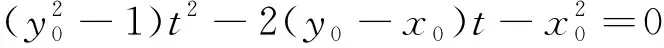
通過上述解答過程,可快速將上述模型進行推廣.例如我們可以得到如下的結論:
結論1 設P(x0,y0)(x0≠2)為圓M:(x-1)2+y2=1外一點,過點P作圓M的兩條切線,設兩條切線與x軸交點的橫坐標分別為t1,t2,若t1·t2=s(s>0),則點P在x2+sy2=s上運動(即其軌跡為橢圓).