深度學習視域下“平面向量的概念”教學設計

周文靜

摘要：隨著新課程標準的頒布與實施，高中數學課堂教學改革有了更加明確的方向，指向學生數學核心素養的培養與發展.數學是一門促進學生思維靈活發展的學科，學習數學時需要進行深度探究、深度思考、深度理解.深度學習理念為高中數學核心素養在課堂中的落地提供了基礎.本文中就深度學習視角下“平面向量的概念”的教學設計進行了探究.

關鍵詞：深度學習；平面向量；教學設計

“平面向量”這樣既具有代數特征又具有幾何特征的概念是學生在以前的學習中沒有接觸過的.學生對平面向量的學習往往流于表面，沒有掌握其本質，因此需要利用深度學習理論，對“平面向量的概念”的課堂教學進行重構.

1 核心概念界定

深度學習是指在教師的引領下，學生對所學習的課題進行深度探索，挖掘數學概念本質，深度理解概念并內化概念，掌握概念的過程.學生通過深度學習后，體會概念生成的路徑，學會挖掘數學概念的數學思想方法.概念深度學習是否發生，主要看是否具備以下幾個特征：一是聯想與建構，把新知與舊知聯系起來，在建構主義學習理論的支撐下，建立自己的知識體系；二是活動與體驗，學生親自經歷數學概念的產生，探索概念的生成過程，形成科學的思維方式；三是本質與變式，能夠抓住教學內容的關鍵特征，全面把握學科知識的本質聯系，在變式中辨析本質特征［1］.

2 “平面向量的概念”教學設計

2.1 聯系生活實際，激發探究興趣

通過生活中的具體情境，降低學生對新授課的恐懼心理，體會數學來源于現實生活，與現實生活緊密聯系，從而提高學生積極探索數學概念的興趣.

教學片段一：創設情境，聯系生活實際

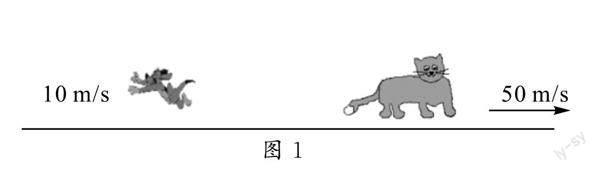
問題1 如圖1所示，貓能捉到老鼠嗎？

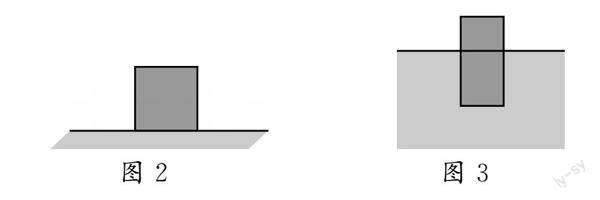
問題2 如圖2所示，物體在地面上受到重力，重力的方向是怎樣的？重力的大小與什么有關？

如圖3所示，物體在液面上受到浮力，浮力的方向是怎樣的？浮力的大小與什么有關？

設計意圖：向量的概念有著豐富的實際背景.通過生活中有趣的“貓捉老鼠”情境，激發學生的學習興趣;通過重力與浮力的大小與方向，引導學生感受向量的物理背景，引出向量的兩個關鍵元素——大小和方向，自然引出本節課的探究內容.

2.2 小組交流探究，體驗概念生成

“經驗是永久的生活老師”，只有體會概念的形成過程，才能深入掌握數學概念的本質.教師層層設問，小組交流，學生挖掘概念.通過自己探索總結出的概念，才能真正將其內化，從而形成合理的認知結構［2］.

教學片段二：層層設問，助力概念形成

問題3 小組合作交流，討論質量、位移、力與速度這四個物理量的異同，總結這四個物理量的相同點和不同點.

追問1：我們從一支筆、一棵樹、一本書中，能抽象出數量“1”.類似地，可以對力、位移、速度這些量進行抽象，形成一種新的量——向量.

你能總結出向量的概念嗎？

生：既有大小又有方向的量叫做向量.

追問2：向量與數量之間有什么異同？

生：向量既有大小，又有方向；數量只有大小，沒有方向.

追問3：物理學中常稱向量為矢量，數量為標量，物理中還有什么量是向量？你能舉出例子嗎？

設計意圖：找到數量與向量的不同點，深入理解向量的概念，找到與其他學科知識的聯結點，自然地引出向量的幾何表示.

問題4 數量可以用實數來表示，數軸上的點與實數存在一一對應的關系，所以數量可以用數軸上的點來表示，那么，該如何表示向量呢？在小船航行中，我們用一條“帶有方向的線段”來表示小船從A地到B地的位移，那么線段的大小表示什么？箭頭的方向表示什么？

生：找到起點，線段AB的長度表示小船位移的大小，線段AB上箭頭的方向表示小船位移的方向.

教師活動：給出有向線段的概念與表示方法，并指

出可以用有向線段來表示向量.帶領學生一起總結如何用有向線段表示向量.

師：除了可以用有向線段的起點與終點字母來表示向量，還可以用小寫字母a，b，c來表示，注意書中是用印刷體黑體表示.

設計意圖：將“既有大小又有方向的量——向量”從文字語言變成符號語言，體現了數學概念的簡明化與符號化特征，感受數形結合的魅力.

2.3 建構概念體系，感受概念本質

數學概念的順應指出學生需要調節、改變原有的數學認知結構，以便于概括新的數學概念.“平面向量的概念”這節課有很多知識點，對于零散的概念，從核心概念的本質出發，讓學生直觀感受概念的生成，形成系統的知識體系［3］.

教學片段三：概念深化，形成知識體系

問題5 對于兩個向量a，b，當兩個向量方向相同時，如何畫出這兩個向量？兩個向量能否比較大小？

生：向量不能比較大小，因為其方向無法確定.

追問1：如圖4，在單元格中畫出兩個向量A1B1，A2B2，這兩個向量有什么關系？

生：大小相等，方向相同.

師：請給出相等向量的概念.

追問2：表示這兩個向量的有向線段起點位置相同嗎？

生：不相同，可以用一條有向線段表示兩個相等的非零向量.

追問3：與有向線段的起點在哪是否有關？

生：無關，因為向量只有大小和方向兩個元素.

追問4：觀察圖5單元格中的向量CD與A2B2有怎樣的關系？

追問5：相等向量和相反向量與平行向量之間有怎樣的關系？

生：相等向量和相反向量都是平行向量.

追問6：a，b，c是一組平行向量，在一條與a所在直線平行的直線上，能否作出與a，b，c相等的向量？

追問7：相等向量、相反向量、平行向量與共線向量這四者之間有怎樣的關系？

設計意圖：學生直觀感知平行向量、相反向量、相等向量等概念，并理解平行向量、相反向量、相等向量之間的關系，使概念成為學生觀察、比較、抽象、概括后的自然產物.

問題6 本節課你收獲了哪些知識與方法？

設計意圖：課堂小結在教學中起關鍵作用，師生一起總結課堂上收獲到的知識點，不僅僅是為了形成知識體系，更重要的是要讓學生掌握概念的生成過程與本質，感受到探究數學概念的路徑與數學思想方法.

數學概念課是高中數學的重要組成部分，數學概念在學生高中數學學習中起著關鍵作用.對數學概念的本質把握不到位，在數學學習中就會出現本質性的錯誤.很多時候學生在學習數學概念后，只知其然，不知其所以然.在深度學習視域下，通過直觀想象探索平面向量的本質，學生對于數學概念的學習從“淺嘗輒止”到“入木三分”，能達到“知其然，知其所以然，何由以知其所以然”這三個層次.

參考文獻：

［1］易文輝.基于“深度學習”的高中數學教學思考［J］.數學教學通訊，2019（21）：3-5，20，2.

［2］吳友明.基于深度學習的高中數學概念教學實踐研究［J］.中學數學教學，2021（1）：1-5.

［3］林朝暉.經歷概念的形成過程 積累基本活動經驗——以“平面向量的概念”教學為例［J］.中學數學研究，2021（7）：10-12.