好奇心和想象力需要數學活動滋養

仲崇恒

【摘 ? 要】培養好奇心和想象力是新時代對學生核心素養提出的新要求。以“不規則圖形的面積”為主題的項目式學習活動，從培育學生的好奇心和想象力出發，以數學實驗為主要學習手段，以測量工具為思維支點，引導學生在猜、估、比、數、鋪、稱、擲等活動中充分思辨，注重數學知識與方法的層次性和多樣性，從而發展學生的實踐能力和創新精神。

【關鍵詞】好奇心；想象力；不規則圖形的面積；核心素養

好奇心和想象力是人類社會不斷創新和持續前進的基本動力，培養好奇心和想象力是新時代對學生核心素養提出的新要求［1］。心理學研究表明，兒童期是好奇心和想象力培養的黃金時期。然而，在當今學校教育中，學生的好奇心和想象力都在嚴重流失，這一現象令人擔憂。

一、課前思考

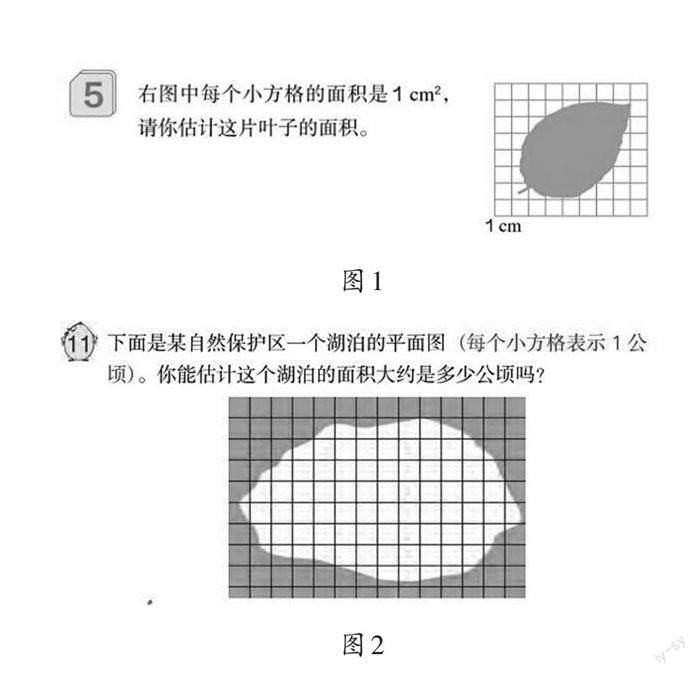
在某校一次學業質量現場考查中，教師拿一片樹葉問學生：“請你估計一下這片樹葉的面積是多少？”學生的第一反應卻是“我們沒有方格紙”。產生這種情況的原因，與當前的主要教學方式息息相關。當前教學中，數方格法是估計不規則圖形面積的主要方法。在現行人教版教材、蘇教版教材中，“不規則圖形的面積”都安排在五年級上冊“多邊形的面積”單元，作為最后一個例題進行教學（如圖1、圖2），教學的基本思路是估計。教學時，教師會為學生提供學具方格紙，讓學生使用方格紙進行估算，具體可分為兩種方法：一是按滿格和不滿一格（按半格算）分類計算，二是將不規則圖形看作近似的平行四邊形或長方形等圖形來估算。教師及學生對方格紙的依賴顯而易見。

教師的教學若想擺脫對方格紙的依賴，開闊學生的數學思維，培育學生的好奇心和想象力，就要努力引導學生探尋其他估計不規則圖形面積的方法、工具。為此，筆者面向六年級學生開展了一次項目式學習活動，以數學探究實驗為主要學習手段，引導學生在對方法、工具的關聯性思考中，深刻體驗數學知識間的聯系、不同學科的整合以及數學與科技、生活的密切關系。具體教學目標如下。

（1）在真實情境中，引導學生主動參與數學探究活動，進一步理解和掌握不規則圖形面積的估計方法，感悟多種方法之間的轉化和聯系，體會“單位面積”作為測量標準的重要性。

（2）通過數學問題的提出和解決，促進學生實現數學思維和閱讀、實驗等學習方式的有效融合，發展學生的好奇心和想象力，提高學生的應用意識和創新意識。

二、教學實踐

（一）創設真情境，叩問學習活動價值

情境認知理論認為，學生在一個完整真實的問題情境中能夠產生學習的需要。因此，教師改變直接教授知識的課堂結構，通過提問激發學生的好奇心，進而確定教學主題。

教學時，教師開門見山地提出問題：“現實世界中有不規則的圖形嗎？”學生舉例說明后，教師追問：“我們需要知道這些不規則圖形的面積嗎？”

接著，教師用課件出示中國最大淡水湖鄱陽湖2022年7月20日和8月19日兩日的衛星圖，基于生活場景引導學生認識測量不規則圖形面積的必要性。之后，教師再次追問：湖泊、森林、拍賣的土地等不規則圖形都很大，它們的面積是如何得來的？

設計意圖：本環節注重真實情境的創設，通過提問層層推進，激發學生的好奇心和求知欲，引導學生體會測量不規則圖形面積的現實意義。

（二）提出新問題，梳理已有解決方法

想象不是憑空發生的，它必須依憑于人的記憶表象和知識結構［2］。因此，在解決問題的過程中，感性、直覺、經驗都是必要的基礎。

教學時，教師讓學生動手做（撕或剪）一個不規則圖形，并提問：這個不規則圖形的面積是多少？測量它的面積需要用到什么工具？學生通過分組討論，交流估計不規則圖形面積的方法和所需的工具。小組交流后，教師追問：“如果沒有方格紙、格點紙，甚至沒有直尺，怎么辦？有沒有其他的工具能幫助我們測量它的面積？”引導學生回溯解決問題的源頭：人身體的各個部位是天然的“尺子”，還可以通過用眼睛看或用手指量來測量。

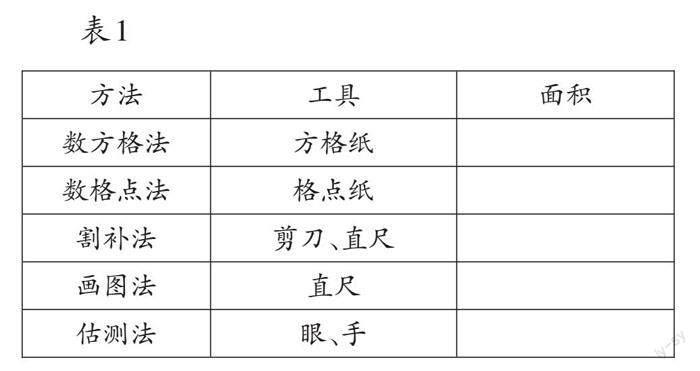
如表1所示，測量不規則圖形的面積主要有以下5種方法。在教師的引導下，學生各選一種方法進行估測，然后比較估計結果，了解方格紙在精確測量面積中的作用。

設計意圖：本環節教師組織學生討論測量不規則圖形面積的方法和工具有哪些。通過問題“如果沒有方格紙、格點紙，甚至沒有直尺，怎么辦？”，啟發學生運用多種方法和工具進行測量，在比較中了解方格紙在精確測量面積中的作用。

（三）巧稱厚紙板，思辨面積和質量的關系

在課堂教學中，教師既要關注學生已有的知識經驗，也要關注學生未知的發展，激發他們的好奇心，啟迪他們的智慧。

教師提問：“如果沒有方格紙怎么辦呢？有人說電子秤也可以用來稱面積，你們覺得可能嗎？”問題一出，學生的好奇心被充分調動起來。學生自然知道電子秤稱出的是質量而不是面積，但老師也不會無的放矢。

師：大家稱一稱各自不規則圖形的紙板有多重。

（學生稱重后，教師選擇兩塊紙板提問）

師：這兩塊紙板，一塊是12.5克，一塊是18.7克，你想到了什么？

生：18.7克的紙板比12.5克的紙板面積大。

生：還需要看紙板是不是同一個品種，不同紙板的密度不一樣。

師：這名同學說到了一個新詞——密度，這是物理學上的一個重要概念。還有誰也理解他的意思？

生：他的意思是說，同一種紙板密度相同，紙板的質量和體積有關系。而當紙板厚度一樣時，體積和底面積有關。

師：這個底面積就是我們要研究的不規則圖形的面積。簡單來說，兩塊紙板的材質和厚度相同，質量大的面積就大。

生：同一種紙板，質量和體積成正比例。現在高度一定，所以體積和底面積成正比例。

師：簡單來說，兩塊紙板的材質和厚度相同，質量大的面積就大。那么，如果想知道這塊紙板的面積到底是多少，用多少克來說行嗎？

生：不行。但我們可以先稱一下面積為1平方厘米的紙板的質量是多少克，再把質量轉換成面積。

師：你們能聽明白他說的意思嗎？大家試試看。如果有更好的方法也可以試試。

（學生以四人小組為單位進行探究，并匯報）

生：1平方厘米的紙板太小、太輕，電子秤顯示不出質量。我們又剪了一個邊長為5厘米的正方形紙板，稱出來是1.1克。

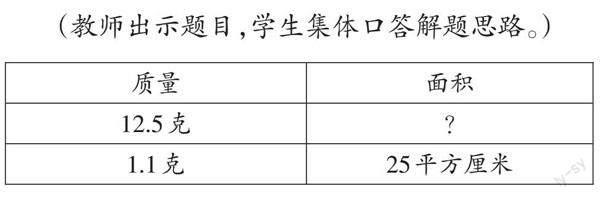
（教師出示題目，學生集體口答解題思路。）

師：大家把稱1平方厘米的正方形紙板，改為稱25平方厘米的正方形紙板，是為什么呢？一定要是正方形嗎？一定要比原來的不規則圖形小嗎？

師（總結）：稱一稱就是在質量和面積之間建立聯系，也是一種轉化，是把一個面積問題轉化為質量問題。無獨有偶，有一個木匠也是用這樣的方法稱出了地圖的面積。大家可以讀一讀數學故事《巧木匠稱地圖》。

設計意圖：培養想象力需要把一些猜想和經驗聯系在一起。電子秤這一工具的出場，立刻讓不規則圖形的面積計算充滿了驚喜和思辨。整個探索過程，從同材質紙板質量與面積的關系切入，然后把稱1平方厘米紙板的質量轉變為稱25平方厘米紙板的質量，最后再轉化為某個具體面積的測量，思維過程層層遞進。

（四）綠豆總動員，破解整體與局部的密碼

奧蘇貝爾認為，學習者把潛在的有意義的學習材料同他們認知結構中的原有觀念建立非人為的和實質性的聯系，就意味著他們能有效地把自己原有的知識作為理解、接受和固定新知識的一種觀念上的有組織的基礎。［3］借助這一基礎，學習材料和認知結構有了新聯系，解決問題的工具和方法也有了新結合。因此，學生在“稱面積”學習中所獲得的新知能激勵他們去發現并接受新挑戰。

師：剛才我們用秤稱出了面積的大小。大家大膽地想一下，還有什么不同的辦法嗎？有人認為綠豆也可以作為測量面積的工具，你覺得可行嗎？

生：可以用綠豆鋪滿圖形，先數出綠豆的數量，再乘一粒綠豆所占的面積。

生：但是不能把綠豆堆在一起，要均勻地鋪滿一層。

（教師出示鋪滿一層綠豆的圖片）

師：怎么做才能得出面積呢？

生：可以將綠豆的圖形變為長方形。

師：用綠豆密鋪的方法求面積要分幾個步驟？

生：鋪綠豆求面積可分為三步：一是將不規則圖形鋪滿一層綠豆；二是移動綠豆，使之變為長方形；三是測量長方形的長和寬，算出面積。

師：如果綠豆不夠多，怎么辦？

生：可以一塊一塊鋪，分別進行測量。

生：這樣太麻煩，誤差會變大。

師：有人就用綠豆在紙上隨手一拋，如圖3所示，這對你有什么啟示嗎？

師：大家閉上眼，想象自己在做拋綠豆測面積的實驗。先把手中的不規則圖形描畫在一張白紙上，再拿出一把綠豆，隨機地將這些綠豆拋在白紙上，然后一粒一粒地數綠豆。好了，睜開眼，歡迎回到課堂！請看數綠豆的結果：白紙上一共有100粒綠豆，其中有35粒在不規則圖形內。

師：有了這些實驗數據，怎么求出不規則圖形的面積？

生：先量出長方形紙的長與寬，計算出面積，再……

（教師出示題目）

[面積 數量 620平方厘米 100粒 ？ 35粒 ]

師：根據表格中的已知條件，你能知道不規則圖形的面積嗎？

生：在拋綠豆測面積實驗中，圖形面積和綠豆數量成正比例，我們可以據此計算出不規則圖形的面積。

師：那拋綠豆測面積實驗是只做一次就夠了嗎？

生：最好多做幾次，做的次數越多，算出來的面積就越接近真實值。

（教師用模擬實驗軟件進行演示，其中拋擲1000000次的結果如圖4所示）

師：通過剛才的數學模擬實驗，你有什么體會和感受？

師：這些求不規則圖形面積的方法有什么共同點？（轉化、單位面積等）如果不規則圖形很大，怎么求面積？這個問題留給大家課后繼續思考。

設計意圖：基于“稱面積”的學習經驗，學生的好奇心和想象力被充分激發。在“用綠豆密鋪的方法求面積”活動中，教師讓學生動手操作，探索數學實驗步驟，用想象實驗（思想實驗）重復測量同一對象獲得數據，從而滲透數據意識。

三、教后反思

“會用數學的思維思考現實世界”是數學課程要培養的核心素養的重要方面，它使得數學課堂追求思維的含量，注重彰顯數學學科的獨特魅力。“不規則圖形的面積”項目式學習活動很好地踐行了這一核心素養，它主要具有如下特征。

（一）素養導向

教師明確以學生為主體的教學目標，以核心素養為導向，建構能夠促進學生思維發展和問題解決的學習任務。教學從真實問題情境出發，從生活場域到平面圖形，從思維方法到活動工具，引導學生逐步深入研究不規則圖形的面積。課堂教學順應學生的心理活動，推行積極思考、動手實踐、自主探索、合作交流等多種學習方式，以便更好地發揮數學的育人價值，使學生通過數學學習獲得更好的發展。

（二）實驗導向

好奇、好問、想象、探究、發現、創造等環節都是密切相關的。好奇心能豐富做一件事的感受。學生在估一估、比一比、數一數、量一量、稱一稱、鋪一鋪、擲一擲等“做中學”活動中充分思辨，充分想象，舉一反三，破而后立。數學實驗活動中，教師組織有方，詳略得當，充分利用數學方法的不同表現形式，靈活運用合適的工具，充分滿足了學生的好奇心，激發了學生的想象力，培養了學生求真務實的學習態度，提高了他們解決實際問題的能力。

（三）問題導向

開放性的問題無疑是思維的激發點。“沒有方格紙怎么辦？”這一問題給學生帶來了困惑，也激發了學生主動探索的欲望。“這些求不規則圖形面積的方法有什么共同點？”這一問題則啟發學生建立不同方法間的內在聯系，也幫助他們理解了知識的結構化。有效的數學課堂教學就是要讓學生沒有問題進來，卻帶著滿腦子的問題離去。“如果不規則圖形很大，怎么求面積？”這一首尾呼應的問題在課堂上其實并沒有解決，卻又似乎已經解決，因為撒下一顆好奇的種子，可以獲得豐碩的思維成果。

“不規則圖形的面積”項目式學習活動，將不同方法、不同觀點、不同經驗聯系起來，打破常見的知識邊界，探索結構化整合，拓展課程內容，適應學生未來的需求。整個教學過程注重數學知識的發展性，強調數學方法的層次性，聚焦思維工具的多樣性，有利于培育學生的好奇心和想象力，發展學生的實踐能力和創新精神。

參考文獻：

［1］嚴欣斌.好奇心和想象力：核心素養培育的新視點：以科幻教育為例［J］.中國電化教育，2021（10）：126-132.

［2］潘新和.教育：失去了想象力還有存在價值嗎？（續）［J］.福建論壇（社科教育版），2007（4）：6-11.

［3］王本法.奧蘇貝爾學習類型劃分的理論及其意義［J］.教育理論與實踐，1996（4）：57-60.

（江蘇省昆山市玉峰實驗學校）