基于物理模型建構的解題研究

摘 要：物理解題并不單純是應用物理知識解決物理問題的過程，而是學生針對問題建構物理模型的過程.因此，教師進行物理習題教學前應分析學生基于模型建構的解題過程，發現學生的問題以采取針對性的教學策略.文章依據Gilbert提出的建模模型分析了學生在物理解題過程中可能出現的模型提取問題、模型表征問題和模型評估問題，同時獲得了物理習題教學的兩點啟示.

關鍵詞：物理模型；模型建構；習題教學

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2023）29-0061-04

收稿日期：2023-07-15

作者簡介：劉雨萌（1991.2-），女，黑龍江省佳木斯人，研究生，中學一級教師，從事物理教學研究.

模型建構能力是一種重要的思維能力，近年來模型建構能力已經被寫入多個國家的課程文件中，《義務教育物理課程標準（2022年版）》中也指出，學生要會用所學模型分析常見的物理問題^[1].但實際教學中，很多學生在遇到物理題目時往往感覺無從下手，究其原因是學生無法從物理習題情境中準確構建物理模型.因此，有必要分析和梳理物理習題解決過程中的模型建構活動，從而為物理習題教學提供啟示.

1 物理模型建構的內涵

物理模型建構的內涵中包含了兩個要素，一是模型建構活動，它往往發生在問題解決過程中，用來簡化和整理對物理問題的思考；二是模型建構結果，即物理模型，它是建模者的思維指向，即形成物理對象或物理事件的關鍵結構，包括空間結構、物理過程、物理屬性等，這些關鍵結構能起到替代物理對象的作用，從而簡化思維的工作任務.總的來說，物理模型建構是物理問題解決中的重要思維活動，是建模者在解決物理問題過程中，為了簡化物理問題、抓住問題的主要矛盾而在頭腦中建立物理對象或物理事件的關鍵物理過程、物理屬性、物理空間結構等的科學思維活動.

2 基于物理模型建構的解題過程

關于模型建構過程的研究在上世紀八十年代已經在國外展開，Hestenes、Clement、Gilbert等研究人員均提出了自己的觀點.其中Gilbert和Justi在Clement基礎上提出的建模模型是科學課程經常采用的模型之一^[2].他們認為模型建構包括四個階段，如圖1^[3]所示，基于這一過程能夠啟發我們認識到學生解答物理習題的規律.

根據這四個階段可知，當學生解答物理習題時，他們首先會一邊理解習題一邊從記憶中搜索和選擇可用的模型素材和經驗依據來建立一個關于問題的心理模型；其次，學生會使用合適的表征方式將心理模型表達出來；再次，學生通過反思來評估模型與情境的一致性，并隨時進行修改，當學生認為模型符合情境時，就可以應用模型來解答問題；最后學生通過解答習題明確了模型應用范圍，從而可以嘗試將這一模型遷移到類似的物理習題中，整個過程既是解題活動同時也是模型建構活動^[4].

3 學生基于模型建構的解題案例分析

學生在解題的過程中會由于缺乏模型建構的意識和能力而出現各種問題，下面以三個不同領域的習題為例進行具體分析.

3.1 力學習題案例分析

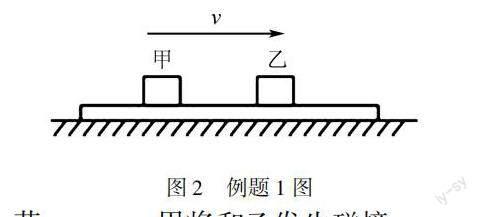
例1 質量分別為m₁、m₂的甲乙兩個物體，放在表面光滑且足夠長的木板上，隨木板一起以水平向右的速度做勻速直線運動，如圖2所示，當木板突然停止時，以下說法正確的是（）.

A．若m₁＞m₂，甲將和乙發生碰撞

B．若m₁＜m₂，甲將和乙發生碰撞

C.若m₁=m₂，甲將和乙發生碰撞

D.無論兩個物體質量關系如何，都不會碰撞

答案解析 此題考查學生對牛頓第一定律的理解，找出題目中的關鍵詞“光滑”說明物體不受摩擦力，“勻速直線運動”說明物體處于平衡狀態，在水平方向上不受力，那么原本運動的物體就會保持原有的運動狀態，因此，甲乙兩物體都以原有的速度繼續做勻速直線運動，此時需要學生在腦海中建構一個“勻速直線運動”的物理模型，那么各自做勻速直線運動的兩個物體，速度相同，永遠不會碰撞，故此題正確答案D.

基于模型建構的學生解題分析：一些學生會選擇A選項，為什么他們會認為如果甲的質量更大就會撞上乙呢？這需要結合學生的模型建構過程進行分析：在學生以往的經驗中，由于慣性，質量大的物體不容易停止運動，質量小的物體則相反.因此，他們根據生活經驗建立了木板停止后的甲運動將比乙快的錯誤模型.這說明學生在建立模型時僅根據生活經驗而缺少對學習過的模型素材的提取和運用，也就是說，他們并沒有正確地提取和運用牛頓第一定律，因此忽略了試題中所包含的“甲、乙水平方向上不受力”的條件，未能建立甲和乙將繼續保持勻速運動的模型.

3.2 光學習題案例分析

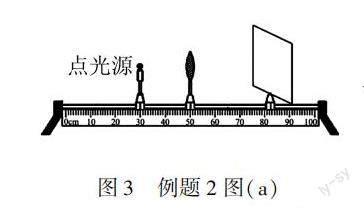
例2 學過透鏡知識后，小明所在實驗小組在光學實驗室（暗室）想對學過的知識進行深入研究，可用的器材有：光源S（視為點光源）、圓形凸透鏡（直徑為）、光具座、光屏（足夠大）.如圖3所示，將光源、凸透鏡和光屏放在光具座上，調節高度，使光源和光屏的中心在凸透鏡的主光軸上.將光源S置于凸透鏡的左焦點處，左右移動光屏，小明發現在移動光屏的過程中，在光屏上光斑外側還有一個暗環，他猜想可能是凸透鏡的邊框造成的，于是他拆除邊框直接將凸透鏡固定在光具座上，進行實驗驗證，發現暗環仍然存在，你認為暗環是如何形成的？若光源S在左焦點上，光屏在右焦點處，如圖4所示，請你算出此時暗環的面積等于多少？

答案解析 此題考查了學生對光經過凸透鏡時所走的光路的理解和繪制，如下圖5所示：從S發出的光，以A、B為臨界點，經過A點之上的沿直線傳播到C點之上，同理經過B點之下的沿直線傳播到D點之下，而經過A、B兩點之間的光經過凸透鏡的折射，折射光線的方向平行于主光軸，位于MN之間，因此，沒有光照到CM和ND之間，凸透鏡是一個圓形的透鏡，即形成一個圓形暗環，如下圖6所示.故暗環的形成是透鏡外側沿直線傳播的光與經透鏡折射的光在屏上形成的無光區.暗環的面積即圖中的陰影面積，S_陰影=S_大圓-S_小圓，由圖6可知，小圓半徑等于透鏡半徑，為?d ，因光屏在右焦點處，故依據相似三角形的知識可知，大圓半徑為d，可得S_陰影=S_大圓-S_小圓=πd²-π（?d）²=?πd²

基于模型建構的學生解題分析：對于這個問題很多學生往往感到無從下手，不明白為何透光的透鏡會形成暗環.那么學生解題的困難主要是什么呢？結合學生的模型建構過程可知，學生的解題困難很可能出現在他對模型素材的提取和模型的表征階段.首先，在模型素材的提取階段，由于用光具座探究凸透鏡成像這一情境對學生來說會在學習凸透鏡成像規律的內容中遇到，因此學生能夠很容易提取光經過凸透鏡的光路模型，但光的直線傳播模型在這一情境中很容易被學生忽略，這導致學生難以理解外圈的暗環從何而來；其次，在模型表征階段這一問題需要學生一邊繪制光路一邊思考，因此學生的另一個困難是他并不知道如何將光路表征出來以輔助他思考問題，比如，雖然學生頭腦中提取了一個模糊的包含光要直線傳播和光經過凸透鏡將會聚的心理模型，但他無法用光路圖來表達光在傳播到凸透鏡邊緣時將經過怎樣的路線.因此，無法準確表征可能是學生解答此題的另一個困難.

3.3 電學習題案例分析

小明打算只利用電流表來測量小燈泡的額定功率，小燈泡的額定電壓為2.5 V，他增加了一個阻值為10 Ω的定值電阻R₀和兩個開關，設計了如圖7所示電路，請將電阻R₀、電流表和燈泡的符號填入虛線框中以便完成實驗.

答案解析 此題考查學生對缺電表電路的設計.器材中沒有電壓表，因此需要設計用已有器材替代電壓表，依據公式U=IR，可以將電流表與定值電阻串聯后當作電壓表使用，將其與小燈泡并聯便可測量小燈泡兩端的電壓，此時開關S₁斷開，S₂閉合，燈的電壓即為定值電阻與電流表示數的乘積，由此確定了小燈泡的位置在X，而定值電阻和電流表的位置還需進一步分析.為測得小燈泡的額定功率，第一步要使小燈泡正常發光，調節滑動變阻器，直到電流表的示數為I=U/R=2.5 V/10 Ω=0.25 A時，小燈泡的電壓達到額定值2.5 V正常發光，第二步根據P額=U額I額，還需測出此時的電流I額，而為使小燈泡始終正常發光，小燈泡與電阻的連接情況應保持不變，即開關S₁閉合，S₂斷開后，小燈泡與電阻仍然保持并聯的連接方式，只有定值電阻在Y位置，電流表在Z位置才能夠做到，因此電路連接應如圖8所示，讀出此時電流表的示數I總，I額=I總-0.25 A，故小燈泡的額定功率為P_額=2.5 V（I_總-0.25 A）.

基于模型建構的學生解題分析：缺電表的電路設計一直是學生較為迷茫的一類題目，究其原因一方面學生缺少用已有模型素材構建新模型的能力，在本題中學生無法構建電流表和定值電阻串聯的電壓表替代模型；另一方面還包括學生模型評估能力較弱，在本題中，一些學生不能從一個假設去推理內部一致的電路模型，比如，假設小燈泡位置正確，在X位置，而定值電阻在Z位置，電流表在Y位置，學生很難從這一電路模型中評估其是否能夠測量小燈泡的額定功率，由于學生不能尋找電路模型與問題情境的一致性，導致其無法構建正確的模型.

4 對物理習題教學的啟示

4.1 依據模型建構過程系統分析學生的解題困難

根據上述分析可以發現，學生在解題中遇到的困難并不是單一由于某個知識點不理解造成的，而是在學生建構心理模型時的復雜的、多階段的問題，教師在習題教學時應該結合學生的模型建構過程具體梳理其解題思維、系統分析解題困難.要做到這一點，教師需要了解學生模型建構的一般過程并具有學生常見解題困難的經驗積累，在此基礎上建構學生解答習題的思維活動，包括思考學生解答習題需要提取哪些生活經驗和模型素材，學生需要如何建立和表征模型，學生要如何通過思維實驗及批判性反思去驗證模型內部及模型與問題情境的一致性，最終學生能夠從習題中總結什么模型素材并用于解決新問題.通過這樣的梳理教師就能夠結合每個學生的解答情況具體分析其解題困難出現在哪個階段，具體方法可通過評價學生解答結果、對比不同學生的答案、觀察學生課堂反饋和針對結果進行訪談等.

4.2 針對學生在解題中的模型建構問題設計應對策略

掌握了學生解題過程中建構模型的具體問題，就能據此設計針對性的教學策略.一是，對于學生模型提取階段的問題，教師應鼓勵學生運用物理語言和生活經驗解釋問題情境，引導學生建立物理概念、經驗直覺同問題情境間的聯系^[5]；二是，對于模型表征階段的問題，教師應該引導學生用多種方式清晰地表達和解釋想法，盡量用可視化的方式輔助模型建構思維^[6]；三是，對于模型反思階段的問題，教師應引導學生嘗試用多個模型匹配情境，訓練學生運用如果……那么會發生……的思維實驗去推理不同模型與問題情境是否適配，以發展對模型一致性的評估能力；四是在模型總結與遷移階段，教師不是單純的進行知識點總結，而是從基于模型建構的解題過程進行系統的總結，比如總結情境與模型間常見的關聯是什么，某一類問題常用的表征方式是什么，模型與情境的一致性思考途徑是什么，等等，這些是學生進行習題遷移的重要思考工具和基礎.

總的來說，學生在解題過程中并不單純是知識的運用，而是基于自身的經驗和模型素材對情境中的問題進行的模型建構過程.在新課程背景下，教師對物理習題的理解和教學應跳出簡單的內容教學的限制，從更復雜的思維與知識的關聯出發，系統分析解題困難、設計教學策略，最終提升學生的物理學科核心素養.

參考文獻：

[1] 中華人民共和國教育部.義務教育物理課程標準（2022 年版）[M].北京：北京師范大學出版社，2022.

[2] 張靜.基于心智模型進階的物理建模教學研究[M].南寧：廣西教育出版社，2020：69.

[3] Justi R S， Gilbert J K.Modelling， teachers' views on the nature of modelling， and implications for the education of modellers[J].International Journal of science education， 2002， 24（4）：369-387.

[4] Gilbert J K， Justi R.Modelling-based teaching in science education[M].Cham， Switzerland： Springer international publishing， 2016.

[5] Cheng M F， Brown D E.Conceptual resources in self‐developed explanatory models： The importance of integrating conscious and intuitive knowledge[J].International Journal of Science Education， 2010， 32（17）： 2367-2392.

[6] Gilbert J K， Justi R. Modelling-based teaching in science education[M].Cham， Switzerland： Springer international publishing， 2016.

[責任編輯：李 璟]