探討項目教學法在中職數學職業(yè)模塊教學中的應用
曹亞秋

【摘要】項目教學法作為一種強調理論聯(lián)系實際,注重實踐操作的新型教學方式,在我國得到廣泛關注并取得了良好的應用效果.本文以“線性規(guī)劃初步”單元為例,對項目教學法在中職數學職業(yè)模塊教學中的應用效果進行探討.
【關鍵詞】項目教學法;中職數學;職業(yè)模塊教學
中職數學職業(yè)教學模塊中項目教學法的應用,能夠在教學任務分解的過程中引導學生去積極主動地思考,作為一種“行動導向”教學法,能夠促使學生在學習的過程中學會學習、應用、合作、創(chuàng)新,將其引入中職數學課程教學當中,不僅可以激發(fā)學生學習興趣,更能夠增強學生自主探究意識以及合作交流精神,在實踐中促進學生綜合素養(yǎng)的全面提升.
1 項目教學法在中職數學職業(yè)模塊教學中的應用
1.1 成本類問題
例1 某集團積極響應鄉(xiāng)村振興號召,支援新農村建設,計劃在2023年興辦一所義務教育學校,硬件建設投資1200萬元.根據有關規(guī)定,除書本費以及辦公等費用之外,同時也會向學生收取一定的學費,經過綜合評判中學生的學費標準定為600元/年,而高中生所要收取的學費標準定為1500元/年.在農村學校建設的過程中,會受到較多條件的限制,因此本次某集團在投資計劃中預備設置的班級規(guī)模在20-30個自然班級.綜合考慮社會效益和經濟利益,對該地區(qū)教育市場進行調查,得出調查數據見表1,那么在實際的計劃投資過程中需要怎樣進行合理規(guī)劃才能夠保證最大年利潤的獲取呢?
解析 確認項目之后,通過事實的引導確認制約條件為班級數量,由此便以班級數量為變量進行問題解決,結合實際情況設所辦初中班級x個,高中班級y個,則根據已知條件列出如下不等式組:
20≤x+y≤30,28x+58y≤1200,x≥0,y≥0,
由利潤=學費收入-年薪支出,根據班級的數量以及年利潤的計算公式,假設該次學校興建的年利潤為s,則:s=60×0.06x+40×0.15y-2×1.2x-2.5×1.6y=1.2x+2y.
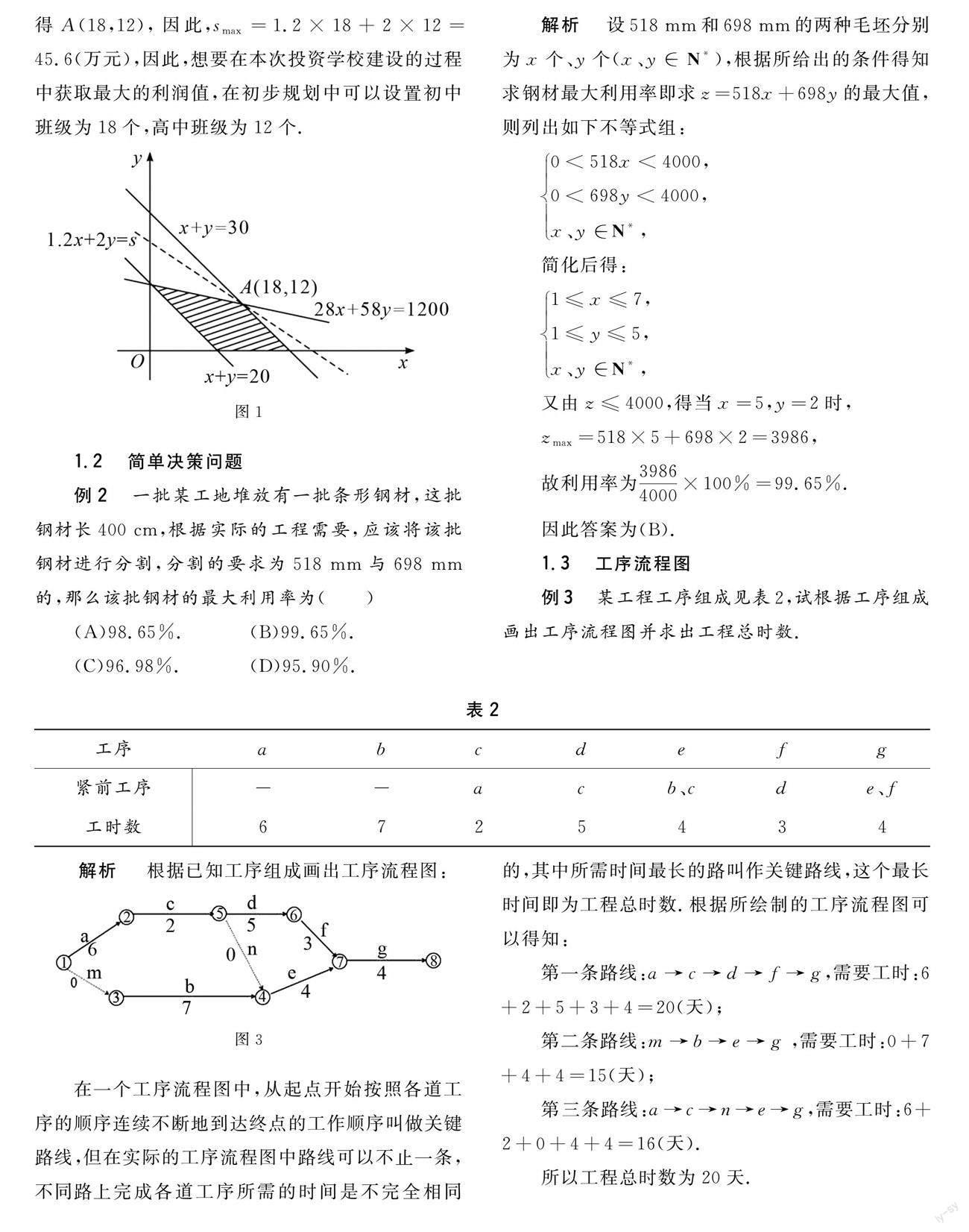
列出不等式組后利用所學知識根據相應數學關系式的建立,畫出相對應的平面區(qū)域如圖1所示.
結合不等式組以及相應的平面區(qū)域圖,可以確定整體利潤直線方程1.2x+2y=s經過點A時能夠實現最大利潤值的獲取,因此:
x+y=30,28x+58y=1200,
綜合以上信息完成二元一次方程組的求解,可得A(18,12),因此,smax=1.2×18+2×12=45.6(萬元),因此,想要在本次投資學校建設的過程中獲取最大的利潤值,在初步規(guī)劃中可以設置初中班級為18個,高中班級為12個.
1.2 簡單決策問題
例2 一批某工地堆放有一批條形鋼材,這批鋼材長400 cm,根據實際的工程需要,應該將該批鋼材進行分割,分割的要求為518 mm與698 mm的,那么該批鋼材的最大利用率為(? )
(A)98.65%.?? (B)99.65%.
(C)96.98%.(D)95.90%.
解析 設518 mm和698 mm的兩種毛坯分別為x個、y個(x、y∈N*),根據所給出的條件得知求鋼材最大利用率即求z=518x+698y的最大值,則列出如下不等式組:
0<518x<4000,0<698y<4000,x、y∈N,
簡化后得:
1≤x≤7,1≤y≤5,x、y∈N,
又由z≤4000,得當x=5,y=2時,
zmax=518×5+698×2=3986,
故利用率為39864000×100%=99.65%.
因此答案為(B).
1.3 工序流程圖
例3 某工程工序組成見表2,試根據工序組成畫出工序流程圖并求出工程總時數.
解析 根據已知工序組成畫出工序流程圖:
在一個工序流程圖中,從起點開始按照各道工序的順序連續(xù)不斷地到達終點的工作順序叫做關鍵路線,但在實際的工序流程圖中路線可以不止一條,不同路上完成各道工序所需的時間是不完全相同的,其中所需時間最長的路叫作關鍵路線,這個最長時間即為工程總時數.根據所繪制的工序流程圖可以得知:
第一條路線:a→c→d→f→g,需要工時:6+2+5+3+4=20(天);
第二條路線:m→b→e→g ,需要工時:0+7+4+4=15(天);
第三條路線:a→c→n→e→g,需要工時:6+2+0+4+4=16(天).
所以工程總時數為20天.

