數學運算素養的水平劃分與評價

李瑛 沈婕 劉勇 王洪亮 譚毅

[摘要]以2022年高考數學（天津卷）實測數據為依據，參照《普通高中數學課程標準》核心素養水平劃分標準，分析考生數學運算素養的發展情況，并針對考生在數學運算素養方面表現出的問題，從明晰運算對象、掌握運算法則、選擇運算路徑、求得運算結果四個方面對高中數學教學提出建議。

[關鍵詞]核心素養；數學運算素養；水平劃分；評價

[中圖分類號]G424.74[文獻標識碼]A

[文章編號]1673—1654（2023）02—001—012

本文為教育部教育考試院“十四五”規劃支撐專項課題“基于學科核心素養的新高考分數標準參照解釋的研究”（課題批準號：NEEA2021043）研究成果之一。

數學學科核心素養是數學課程目標的集中體現，是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現，是在數學學習和應用過程中逐步形成和發展的。包括：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析。這六個核心素養既具有相對獨立性，各自具有鮮明的特征，又組成一個有機整體，具有整合性和綜合性的特點[1]4。核心素養的水平主要表現在學生學習數學和運用數學解決問題的過程中，根據問題解決的情況，可以評價學生相應的發展水平[2]。2022年普通高等學校招生統一考試（天津卷）數學試卷（以下簡稱“試卷”）所考查的核心素養的分布如表1所示。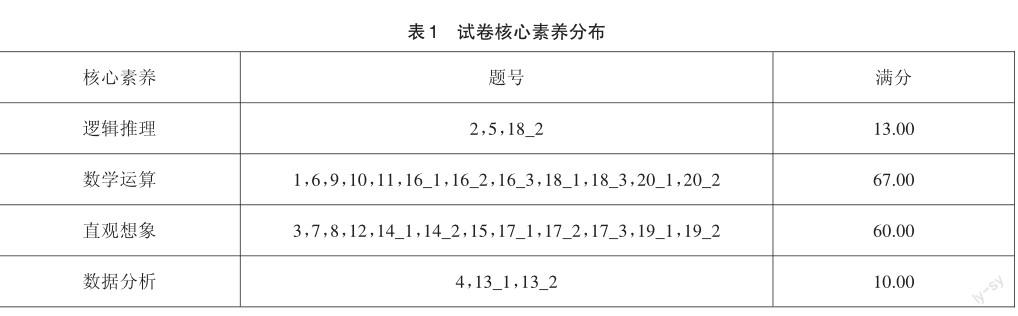

總體看來，試卷突出考查了邏輯推理、直觀想象、數學運算、數據分析四大數學核心素養，數學抽象與數學建模兩個核心素養雖然沒有直接命題考查，但在試卷中也有所滲透。數據顯示，對數學運算素養和直觀想象素養的考查占有較高的比例。

數學運算是數學活動的基本形式，是解決數學問題的重要途經，是獲得問題結果的重要手段，是高中學生應具備的最基本的數學素養。數學運算素養在高考答題過程中的具體表現為：學生在規定時間內理清運算對象的關系，依據數學原理，尋求合理簡捷的運算途徑，應用運算法則解決問題，正確求解寫出規范答案。

以2022年高考考生實測數據為依據，以數學運算的水平劃分為標準，評價考生數學運算素養的發展水平，可以指導教師針對提升學生的數學運算素養水平調整教學方案，實施教學策略，開展教學活動，提升教學效果。

一、數學運算素養的概念及水平劃分

《普通高中數學課程標準（2017版2020年修訂）》（以下簡稱“《課程標準》”）指出：數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的素養。主要包括：理解運算對象、掌握運算法則、探究運算思路、選擇運算方法、設計運算程序、求得運算結果等。數學運算是演繹推理，是解決數學問題的基本手段也是計算機解決問題的基礎。

《課程標準》中將數學學業質量水平分為水平一、水平二、水平三共三個等級，分別對應高中畢業的數學學業水平考試、高考、大學自主招生考試三類不同考試中考生應當達到的要求以及命題依據。高考是基于數學學科核心素養的考試，參考三個維度進行命題。第一個維度是反映數學核心素養的四個方面——情境與問題、知識與技能、思維與表達、交流與反思；第二個維度是反映數學核心素養的四條主線——函數、幾何與代數、概率與統計、數學建模活動與數學探究活動；第三個維度是反映各核心素養的三個水平。

對于數學運算素養，《課程標準》從情境與問題、知識與技能、思維與表達、交流與反思四個方面給出了三種不同水平的劃分標準。具體內容如表2所示。

由表2可以看出，三個水平在難度上雖然逐級遞增，但也體現了整體性和階段性。其中數學運算素養的四個主要表現，即理解運算對象、掌握運算法則、探究運算思路、求得運算結果，在三個水平的階段性要求不同。水平一只要求能夠在熟悉的數學情境中，根據問題的特征形成合適的運算思路；水平二要求在關聯的情境中能夠針對運算問題，合理選擇運算方法，設計運算程序；水平三則要求在綜合的情境中能夠針對運算問題，構造運算程序。

二、數學運算素養試題實測數據分析

依據考生答題的典型表現，將考生水平劃分為“精通水平”“熟練水平”“基本水平”“基本以下水平”四個等級，依次記為G4、G3、G2、G1組，全體考生記為G5組。臨界分數采用安戈夫法來確定，依次為124分、101分、79分，即124-150分為G4組，101-123分為G3組，79-100分為G2組，0-78分為G1組。

試卷考查學生數學運算素養的題目分值為67分，涵蓋了集合的運算、對數運算的性質、三角函數的性質、復數的運算、二項式定理、正余弦定理、數列、導數等多個知識點。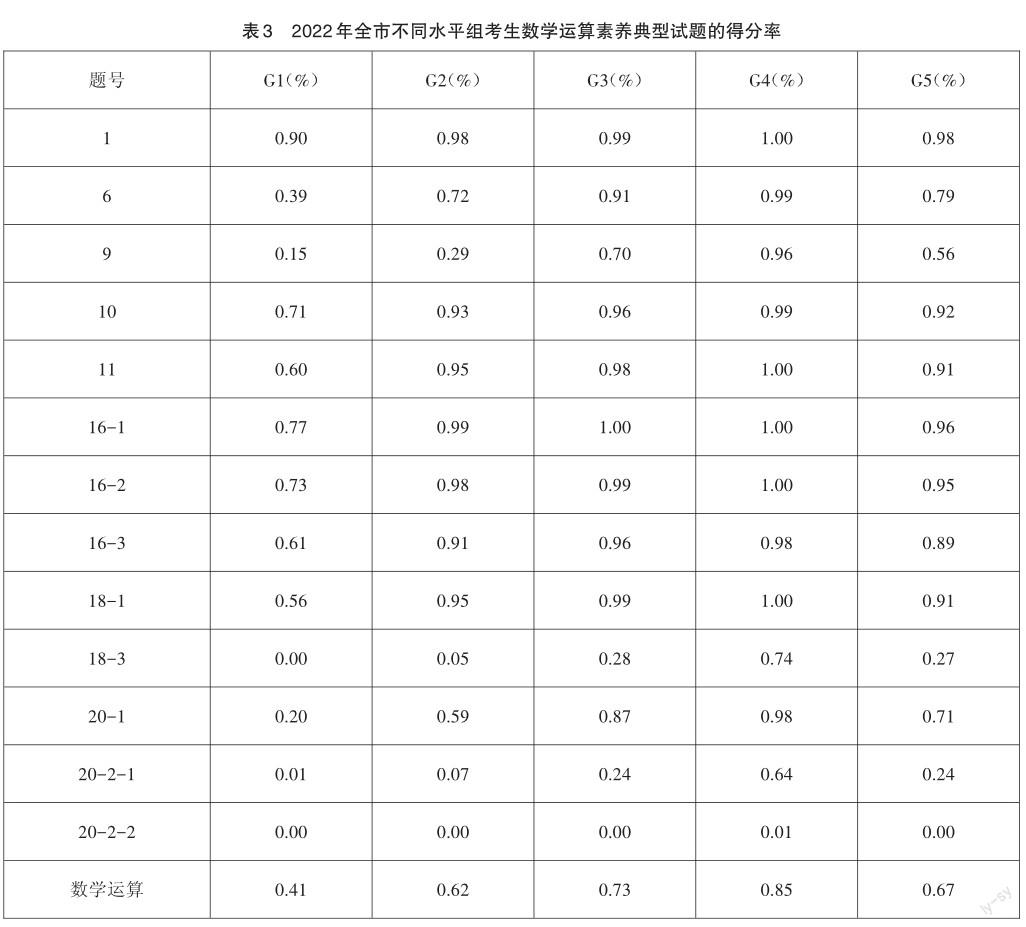

表3反映出2022年不同水平組考生在數學運算素養典型試題的得分率。從數據的具體表現來看，試卷側重考查數學運算素養的題目分布合理，充分體現了基礎知識背景下的素養考核。其中第1題、第10題、第11題、第16題、第18-1題的得分率都比較高，且G2-G4組考生對比沒有明顯差異，說明絕大部分考生對于基本的、常見的數學運算問題能夠達到精通水平，但G1組的表現相對于其他三組存在明顯不足，如第18-1題的得分率僅為0.56。從得分率在0.5-0.8的試題來看，G3和G4組的表現明顯優于G2和G1組，而得分率為0.2-0.3的數據則顯示，四個水平組存在分化過大的現象，值得關注。

下面以第1題、第18題和第20題為例，對數學運算素養的具體考查情況以及考生的數學運算素養發展水平進行分析。

（一）數學運算水平一試題的考查

例題1：試卷第1題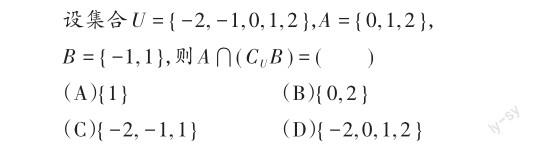

【試題水平劃分】本題用列舉法表示集合，考查了全集的概念以及補集、交集的基本運算。集合中的元素是離散型的，學生利用觀察法或者Venn圖，根據集合運算的概念求解即可，是熟悉的數學情境中的運算問題，屬于數學運算水平一的要求范疇。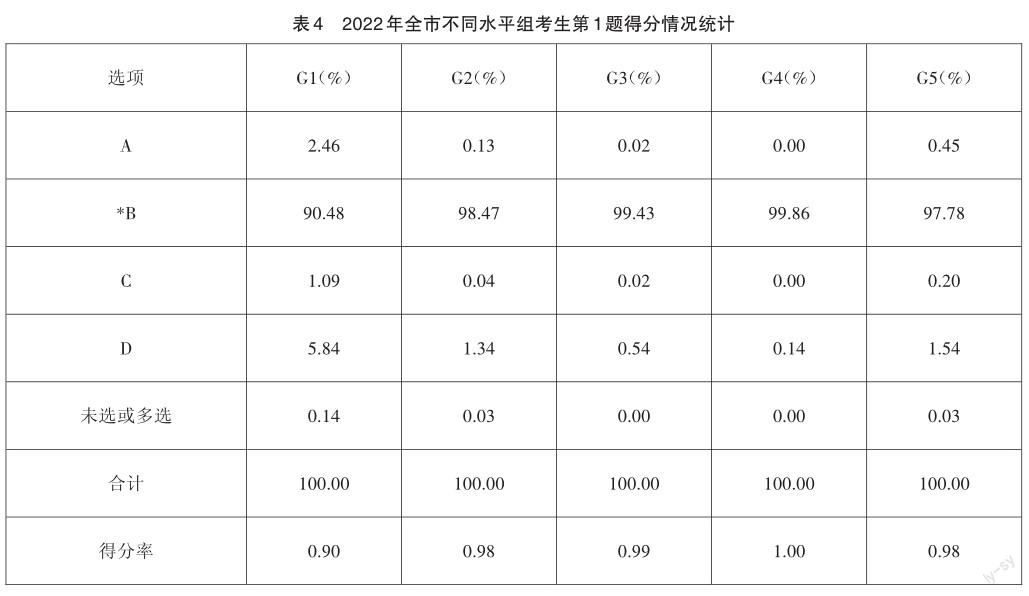

【考生表現】從表4的數據來看，第1題全體考生的得分率為0.98，說明考生對于集合概念的理解以及集合基本運算的掌握還是非常熟練的。由具體數據橫向分析，錯誤選項集中在選項D，顯示部分考生對交集符號“？”與并集符號“？”從認知上產生了混淆；縱向比較可以發現，G4-G2組的得分率都高于0.98，但G1組還是有約10%的考生出現錯誤作答，說明基本水平以下的學生對于集合概念的理解和集合三種基本運算的掌握還有所欠缺。

【教學啟示】集合屬于高考的重點內容，考查穩定，難度較小，常以選擇題的形式呈現，主要是對集合的概念與表示和數集之間的集合基本運算的考查。但集合作為基本的數學語言，能夠簡潔、準確地表述數學研究對象，這就需要在教學中加強這種數學“語言”的使用，讓學生在使用中理解集合的概念、集合間的關系、集合的運算，體會集合這種語言的重要性和必要性。

（二）數學運算水平二試題的考查

【考生表現】第18題的得分率為0.62，本文主要針對考查數學運算素養的第（Ⅰ）問和第（Ⅲ）問的考生表現作具體分析。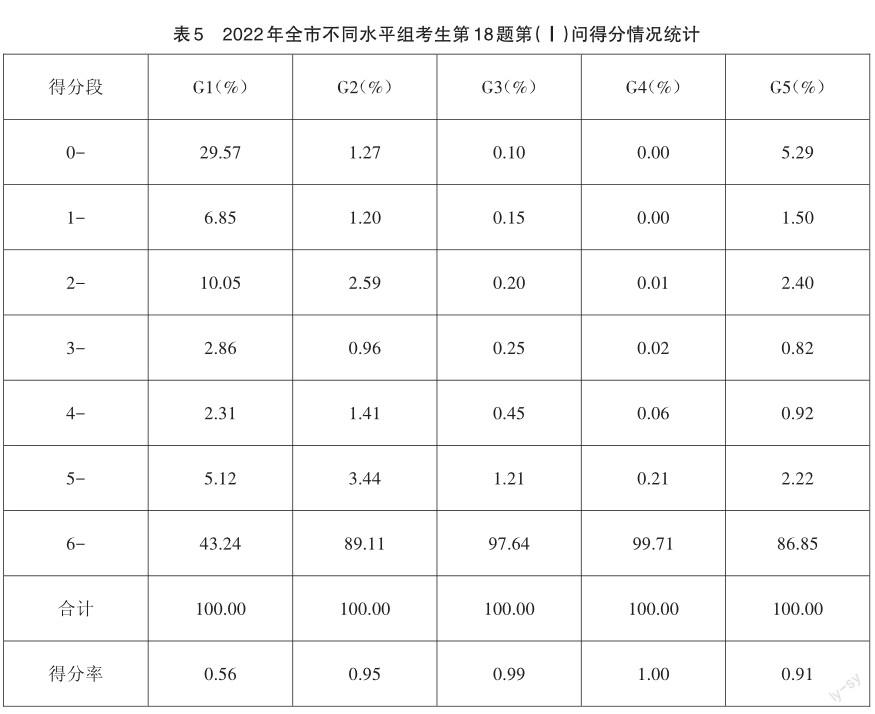

從表5的數據來看，本問全體考生的得分率達到0.91，其中G4、G3和G2組的得分率都在0.95及以上，說明基本水平以上考生的表現還是很突出的。相比而言，G1組表現欠佳，得分率僅為0.56，特別是有接近30%的考生得了0分，這說明基本水平以下考生對于求解數列通項公式這類基本問題仍存在困難，處理方法仍不太明確或者不熟練，在教學中還需要加強訓練。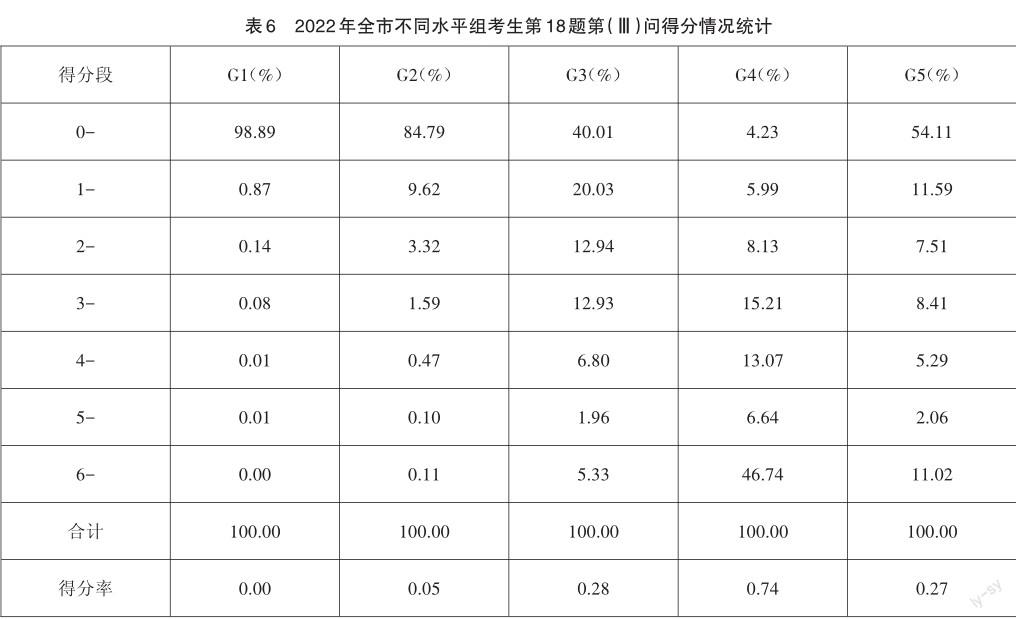

表6數據顯示，第18題第（Ⅲ）問的區分度較好，G4-G1組的得分率依次為0.74、0.28、0.05和0.00。通過對比可以發現，G4組考生表現突出，在綜合情境中表現出了較高的數學運算素養發展水平。

通過抽樣試卷，可以了解不同水平組考生作答本題有以下幾種情況：

【教學啟示】本題啟示教師在數列的教學中要注意以下四個方面：首先，要夯實等差數列和等比數列的基礎知識，掌握數列求和中裂項相消、錯位相減、分組求和、并項求和等基本方法，加強基本技能的訓練；其次，提高學生對抽象數學符號語言的理解和認知，明確數學符號的意義和作用；再次，在不同的問題情境中指導學生積累經驗，建構基本模型，使學生能夠在分析問題、解決問題的過程中及時獲得運算思路，設計運算程序，優化運算方法；最后，要把思維與表達落在實處，不能僅僅“講”思路“說”方法，要幫助學生運用數學的語言準確規范、邏輯嚴謹地表達完整的計算或證明過程。

【試題水平劃分】本題是一道對數學運算素養進行綜合考查的題目，數學運算貫穿于整道題的解題過程。題目綜合考查了函數與導數的基礎知識，主要圍繞導數的幾何意義，利用導數研究函數的極值和零點，以及通過不等式放縮構造新函數，應用函數單調性對不等式進行證明來設計問題。第20題共16分，其中第（Ⅰ）問4分，第（Ⅱ）問的兩小問的分值均為6分，考查了函數思想、化歸與轉化思想，考查了學生的邏輯推理和數學運算兩大核心素養。前兩問達到了數學運算水平二的要求，最后一問屬于綜合情境下的數學問題，通過每一步運算得到的結果提示進行邏輯推理，得到更加準確明晰的運算思路，達到了數學運算水平三的要求。

【考生表現】本題的全體考生得分率為0.27，屬于難題，三問的得分率如表7所示。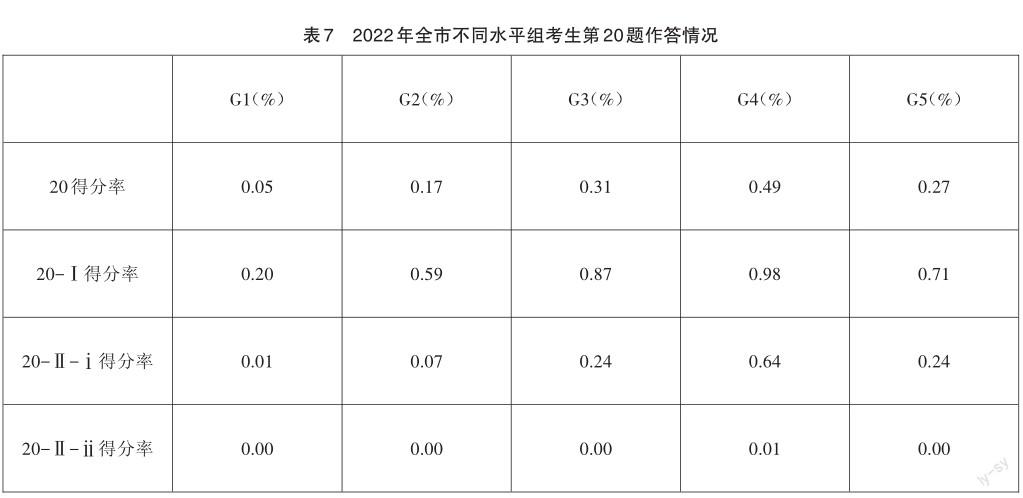

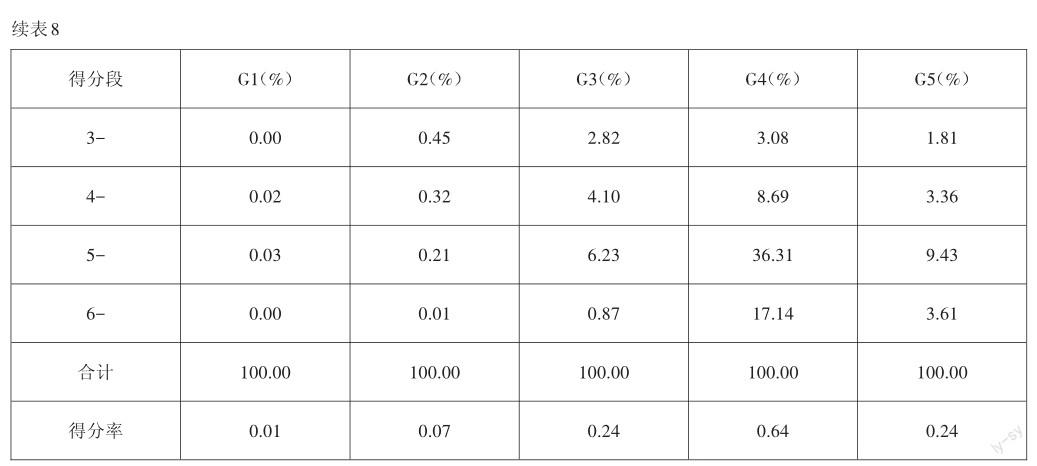
如表8所示，G4組有約36%的考生得到5分，17%的考生得到滿分6分，說明對于這部分同學而言，要繼續加強培養其邏輯推理與數學運算素養；G1組和G2組分別有93.21%和67.77%的考生得0分，說明考生沒有分析題目。

本題最后一問需要考生利用柯西不等式對目標不等式進行放縮，對于一些基本初等函數，如y = ex- （ x + 1），y = x - sinx的性質也需要具備簡單的認識，從而合理規劃運算路徑。由于本問是較復雜的綜合情境，又是試卷的最后一題，在有限的時間內學生難以將所證問題與已知結論或方法等建立聯系，所以各水平組得分率基本都是0。

【教學啟示】高考數學（天津卷）第20題多是考查函數與導數的問題，設計上都比較重視創新性，或問題之間的層層遞進（如2020年和2021年天津卷第20題），或問題情境別有新意[如2019年天津卷（理）第20題]，但都是考查學生的邏輯推理和數學運算核心素養，考查學生構造函數的能力和化歸與轉化的數學思想。本題帶來三點啟示：第一，要引導學生厘清綜合復雜情境中條件和結論之間的關系，培養學生將所證與已知、定理、公理、結論、經驗等建立聯系的能力。第二，重視通解通法的落實，認真研讀教材內容。本題最后一問的放縮利用了柯西不等式，人教版（2019版）數學必修第二冊習題6.3的16題對該不等式的內容用向量的方法給出了證明過程，但教學中往往被忽略或一帶而過。第三，學生在思維和表達的環節中還不夠嚴謹，說明邏輯推理的訓練還不夠系統，這也需要引起教學中的關注。

三、教學建議

（一）加強概念教學，明晰運算對象

明晰運算對象是進行數學運算的重要基礎。這里的“明晰”包括知道、理解兩個層次。這就需要在教學過程中加強概念教學。高中數學有更多更抽象的數學概念，有些概念還容易使學生產生混淆。如例題1中的交集和并集，又如充要條件、充分不必要條件、必要不充分條件等。教師在授課時，對概念要講解清楚，辨析到位。教學中可通過舉反例、類比與對比等方法加強學生對概念的理解。

在高中的數學運算中，運算對象不僅僅是數與式，還包括函數、向量、數列、復數等。因此在運算之前，首先要看清、看準運算對象。其次，要深層次理解運算對象，即了解運算對象的背景，理解運算對象的本質、成立條件、幾何意義、關聯概念及相關數學思想方法等。如“f （ x ）是奇函數”，多數學生想到的只是f （ -x ） = -f （ x ），但還應聯想到其定義域關于原點對稱、圖象關于原點對稱等。因此，在教學中教師應該將概念教學安排在首位，讓學生以理解概念為基礎，指導學生在運算過程中加深對運算對象的再理解、再認識，明晰運算對象的“所指”和“能指”。只有對運算對象及其特征了然于心，明確運算對象概念的內涵和外延，才能在面對運算對象時找準切入點與落腳點，使數學運算自然順暢進行。

（二）夯實基礎知識，掌握運算法則

掌握運算法則是開展數學運算活動的重要保證。高中數學中，不同的運算有不同的運算法則或運算規律，例如集合的運算、函數運算、三角運算等。運算對象不同，則運算法則也存在明顯的差異。

因此，教學中需要注意以下三點：第一，圍繞運算對象指導學生總結相關的運算法則，借助圖表培養學生勤梳理、勤思考的習慣；第二，結合教學內容設計相關問題情境，為學生提供運用運算法則解決問題的機會，在實踐中提高學生應用法則的熟練程度；第三，注重基礎知識的講解，從算理上讓學生理解數學運算法則，使學生不僅“知其然，知其所以然”，更能“何由以知其所以然”。

（三）嘗試一題多解，選擇運算路徑

運算路徑是數學運算的核心所在，教會學生選擇運算路徑是解決數學問題的關鍵。2021與2022年高考數學（天津卷）平面解析幾何解答題都聚焦于直線與橢圓相切的位置關系。從作答情況來看，很多考生在模式化的訓練中，陷入了思維固化的困境。面對試題，遇到了“算什么”“怎么算”“算不對”等諸多問題。

選擇合適運算路徑的前提是要理解題意，明確運算對象，知曉運算法則，要能進行概念、定理、性質之間的相互轉化。要在從“問題”開始，到“問題”結束的過程中，指導學生探究解題思路，選擇運算路徑。教學實踐中可以引導學生提出以下問題：已知條件是什么？得到結論需要什么條件？二者之間的關系是什么？此題與以前做過的哪些題類似？解決這類問題的途徑有哪些？在這個過程中，切忌以教師的認知結構去代替學生的認知，以教師的解題習慣等同于學生的習慣。

另外，一題多解是優化運算路徑的行之有效的方法。如前文所示18題第（Ⅲ）問數列求和的不同方法。教學中要多創設適宜學生思維發展的問題情境，激發學生的創新思維，深化學生對問題的理解，優化運算思路，提升學生解決問題的能力，使學生在探究不同運算思路的過程中積累數學活動經驗，為設計合理簡捷的運算路徑做出鋪墊。

（四）規范解題步驟，求得運算結果

求得運算結果是實施數學運算的最后一步。對于學生數學運算素養的培養不僅要關注知識、技能、思維，還要關注表達能力。通過對試卷的抽樣分析可以發現，學生對綜合情境下主觀題的表達普遍表現較弱，解題步驟與過程的規范性也有所欠缺。因此，教學中除了關注學生在數學運算演繹推理中表現的深刻性、新穎性等思維品質，也要關注學生在運算過程和結果表述中的嚴謹性與準確性。

教學中可以發現，多數學生對運算問題不夠重視。對于簡單的問題表現得眼高手低，認為只要想想思路就解決了問題，不能靜下心來一算到底；對于復雜的問題又表現得缺乏自信、畏首畏尾，不肯花時間去探究，考試時遇到類似問題就直接選擇放棄。因此，在教學過程中，教師不能只給出解題思路，也不能總是由教師示范表達，應當突出運算作用，給予學生足夠的運算機會及運算指導。要讓學生主動參與，并獨立完成規范表達。要利用課堂教學強化學生的運算能力，提高其嚴謹的表達水平。同時，要指導學生養成對運算結果進行分析與反思的習慣。通過運算結果對數學問題進行檢查和驗算，這不僅是數學運算的必要步驟，也是對知識再鞏固的過程。

數學運算素養在高考中是重點考查的數學學科素養，且多以數學核心素養水平劃分中“水平二”的要求為目標。高三學生大多已具備較好的運算基礎、認知水平和數學素養水平，建議教師在教學中多創設關聯情境和綜合情境問題，關注明晰運算對象、掌握運算法則、選擇運算路徑、求得運算結果四個環節，讓學生在數學運算的過程中養成敢質疑、善思考、規范嚴謹的科學態度，從而有計劃、有目的地落實和提升學生的數學運算素養水平。

參考文獻：

[1]中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）[M].北京：人民教育出版社，2020.

[2]譚毅，沈婕，劉勇，等.直觀想象素養的水平劃分與評價——以2021年高考數學（天津卷）為例[J].考試研究，2022，（3）：1-10.

Level Division and Assessment of Mathematics Operation Literacy

Li Ying1Shen Jie2Liu Yong3Wang Hongliang4Tan Yi5

1 Tianjin Experimental High School，Tianjin，300074 2 Tianjin Academy of Educational Science，Tianjin，300191 3 Tianjin Binhai Hangu No. 1 Middle School，Tianjin，300480 4 Tianjin Yaohua High School，Tianjin，300040 5 Tianjin Nankai High School，Tianjin，300100

Abstract：Based on the actual data of the Mathematics Test of Tianjin College Entrance Examination in 2022，this paper analyzes the development of studentscore mathematics literacy with reference to the level division of High School Mathematics Curriculum Standards. In view of the problems students are faced with in Mathematical Operation Literacy，the paper puts forward some suggestions about the math teaching in senior high from four aspects：explicating mathematical operands，mastering the algorithm，selecting mathematical operation path，and getting the operation results.

Key words：Mathematics Core Literacy，Mathematics Operation Literacy，Level Division，Assessment

（責任編輯：吳茳、許志勇、白云）