利用“WinFR界面版” 恢復文件更簡單
天涯衰草
“ Win FR界面版”需要Windows File Recover y的支持,所以先要在Windows應用商店中搜索并安裝WindowsFile Recovery(圖1)。安裝完后到“https://www.disktool.cn/recover y/winfr.html”下載并安裝“WinFR界面版”。注意,Windows File Recovery只支持Windows 10 2004及更高的版本,因此“WinFR界面版”也只能在這些系統中恢復文件。
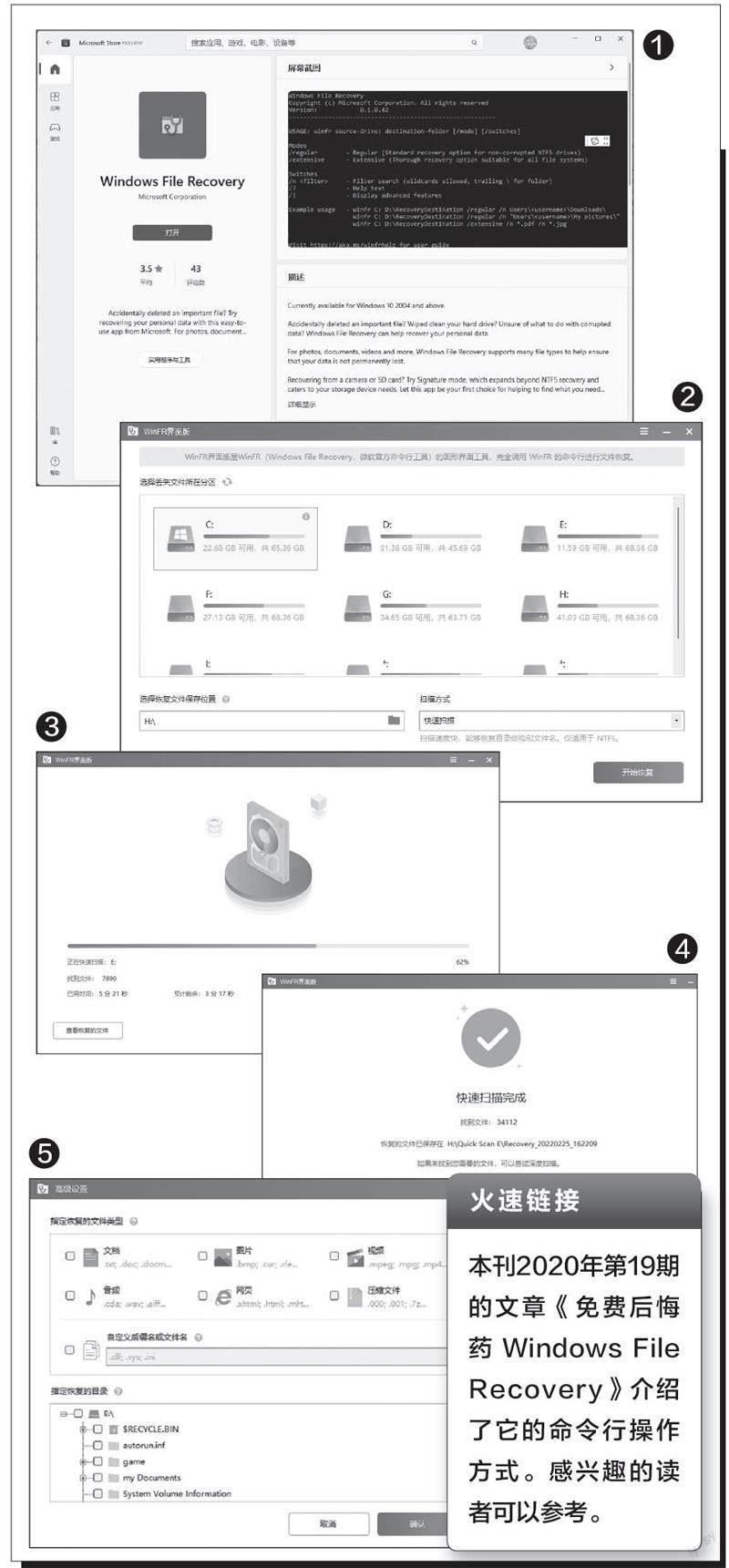
啟動“ Win FR界面版”后,在打開的主界面中可以看到本機所有磁盤分區的名稱。選中丟失文件所在的分區(圖2),接著點擊“選擇恢復文件保存位置”選項后面的瀏覽按鈕,在彈出的對話框中設置恢復文件的保存目錄,然后在“掃描方式”下拉列表中選擇一種掃描方式,一般選擇“快速掃描”就可以。最后點擊“開始恢復”按鈕,在彈出的窗口中就會開始掃描選定的磁盤分區,實時顯示找到的文件數目、已用時間、預計時間等信息(圖3)。該工具的掃描和恢復是同步完成的,待提示掃描完成后,點擊右下角的“查看恢復的文件”按鈕,即可在上述設定的保存目錄中查看到所有被恢復的文件(圖4)。假如使用快速掃描方式沒有找回丟失的文件,那么可以切換到“深度掃描”方式重新操作一遍。
上述的方法操作簡單,但會掃描磁盤分區中所有被刪除的文件,花費的時間較多。如果只想有針對性地恢復某些文件,那么可以點擊主界面左下角的“高級設置”按鈕,在彈出的窗口中的“指定恢復的文件類型”處勾選文件類型,也可以勾選“自定義后綴名和文件名”選項,然后輸入文件類型的后綴名(可同時恢復多個文件類型,后綴名之間用英文的分號隔開)。或者直接在“指定恢復的目錄”處選擇想要恢復的文件夾(圖5)。完成所有的設置后點擊“確定”按鈕,會返回到它的主界面,再點擊“開始恢復”按鈕就可以了。

