善用回歸策略，提升數學解題能力

夏世中

摘要：在九年級緊張的復習階段，教師若善用回歸策略，緊扣數學本質，能引導學生在茫茫題海的探尋中讓數學知識得以鞏固，在追根溯源中讓數學理論得以歸真，在解題總結和反思中讓數學思想與方法得以彰顯，從而有效提升解題能力.

關鍵詞：復習；回歸；原型；數學思想與方法

在九年級復習階段，尤其在各類考試之前，許多學生都會陷入題海無法自拔，只重視解題的數量而忽視解題的質量，只重視解題的結果而忽視解題的過程，只忙于解題而忽視解題后的反思，尤其是對于題中考查的知識點、數學思想方法等數學本質方面的思考幾乎為零.這種為了解題而解題的做法不僅消耗了學生大量的精力，浪費了寶貴的時間，而且復習效果甚微，也在一定程度上制約著學生解題能力的提高.

那么，結合九年級復習的特點，如何有效解題才能更好地提升復習的效果和學生解題能力呢？筆者認為，回歸策略是一種行之有效的策略.九年級的復習是一個龐大的系統，在復習中，要讓學生回歸數學本質，如回歸基礎知識、基本原型、基本思想與方法等，并以此指導解題，在解題之后進一步反思，以促進對知識的理解和內化，形成數學觀念，提升解題的思維能力.從數學的本質特征來說，可以把回歸的方法細分為回歸定義、回歸基本原型、回歸數學思想與方法三種，下面具體談談每種方法的應用.

1 回歸定義

概念是構成學科的基石，定義是對一個概念的內涵和外延所作的簡要而準確的描述，反映了知識點的本質屬性.“回歸定義”實質是以定義為核心知識點，用定義的本質來解決數學問題的方法，是一種樸素又重要的回歸方法.核心概念、重要定義向來都是中考試題的重要考點，在突出考查數學的本質與基礎的同時，也引導著教與學要回歸本源，重視對基礎知識和基本技能的夯實.

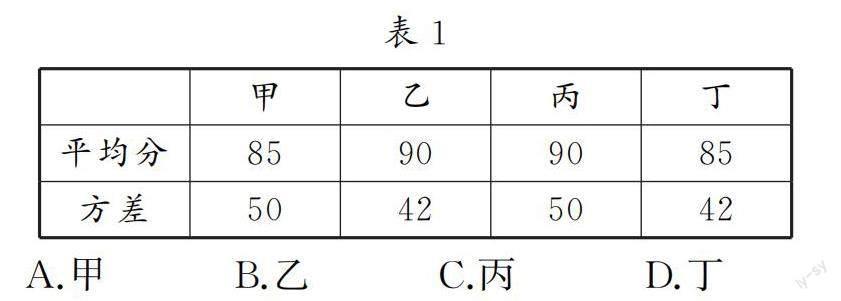
例1 （2020湖北黃岡中考試題）甲、乙、丙、丁四位同學五次數學測驗成績統計如表1所示，如果從這四位同學中，選出一位同學參加數學競賽.那么應選（）去.

A.甲 B.乙 C.丙 D.丁

分析：本題主要考查平均數、方差的定義.先看平均數，平均數大的同學其成績相對較好，若平均數相同，則選擇方差小的同學.方差是反映一組數據的波動大小的量.方差越大，則數據與平均值的離散程度越大，穩定性也越??；反之，方差越小，數據與其平均值的離散程度越小，穩定性也越好.所以乙的成績好且穩定.故選：B.

概念和定義是數學本質的根本，熟練掌握它們的內涵與外延，是深入理解數學本質的基礎，是起決定性作用的第一步，因此教師要予以重視并引導學生進行靈活運用.

2 回歸基本原型

著名數學家華羅庚曾經說過，對于復雜的問題要善于退，直到退到不能再退為止，再從此出發向前推進.九年級的復習中，有大量的綜合題型，對于這類復雜的數學問題，要化繁為簡，化未知為已知，找出其中的原型.當然回歸原型，不光可以把復雜的問題轉化為基本問題，也可以是把復雜的圖形轉化為基本圖形，還可以是把復雜的方法轉化為基本的方法.這樣一個撥云去霧溯根源的過程有利于我們深入理解數學問題，抓住數學本質，達到解一題通一類的復習效果.

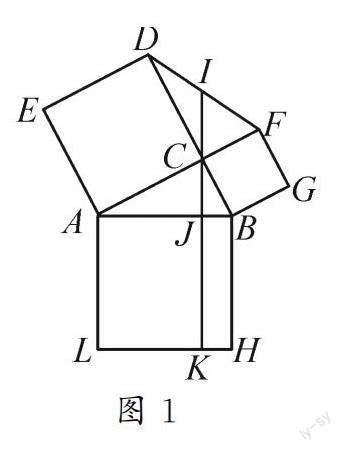
例2 （2022年武漢市中考題）如圖1，在Rt△ABC中，∠ACB=90°，AC>BC，分別以△ABC的三邊為邊向外作三個正形ABHL，ACDE，BCFG，連接DF.過點C作AB的垂線CJ，垂足為J.分別交DF，LH于點I，K.若CI=5，CJ=4，則四邊形AJKL的面積是___________.

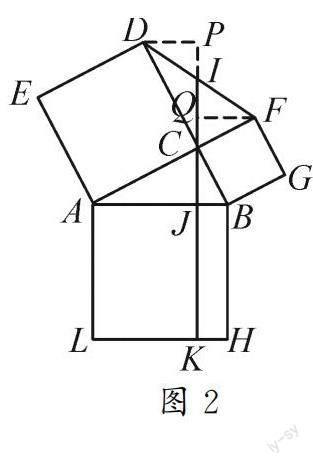
分析：如圖2，過點D作DP⊥CI，交CI的延長線于點P，過點F作FQ⊥CI于點Q.通過作兩條垂線，構造兩組全等三角形△ACJ≌△CDP（AAS）和△BCJ≌△CFQ（AAS）.因此借助全等三角形實現線段長度關系的轉移，AJ=CP，DP=CJ=4，BJ=CQ，QF=CJ=4，所以DP=QF，從而△DPI≌△FQI（AAS），所以DI=FI，PI=QI.因為∠DCF=90°，所以DI=FI=CI=5.

在Rt△DPI中，由勾股定理可得PI=3，所以QI=PI=3，于是AJ=CP=CI+PI=5+3=8，從而BJ=CQ=CI-QI=5-3=2，則AB=AJ+BJ=8+2=10.因為四邊形ABHL為正方形，所以AL=AB=10.又四邊形AJKL為矩形，故四邊形AJKL的面積為AL·AJ=80.

由圖2可以總結出以下幾個結論：（1）S_△ABC=S_△DFC；（2）若IJ⊥AB，則DI=FI，AB=2CI；（3）若DI=FI，則IJ⊥AB，AB=2CI.回歸到以往的解題經驗，發現這類幾何圖形還有其他的形態.如圖3，把兩個正方形換成兩個等腰直角三角形；如圖4，把兩個正方形換成兩個相似直角三角形；等等.它們的相關結論也是成立的.

多組相似的幾何圖形必然是由某個原始的幾何模型衍生和變形得到的，通過尋根溯源，我們發現這一模型來源于七世紀印度數學家婆羅摩笈多（Brahmagupta）的一個定理：如果一個圓內接四邊形的對角線互相垂直相交，那么從交點向某一邊所引垂線的反向延長線必經過這條邊對邊的中點.由該定理衍生了一系列的幾何圖形，其模型的結論當然都成立.至此，學生豁然開朗.盡管圖形有著七十二變的魔力，但是總也逃不出我們的掌心，我們有復原它的能力，讓其回歸本真，各個擊破.

3 回歸數學思想與方法

雖然九年級的復習內容多而雜，但是眾多的內容所反映出的數學思想與方法卻十分有限.比如，在初中階段由一次函數、二次函數、正比例函數、反比例函數的概念和性質所提煉出的思想都叫做函數思想，方程知識對應的是方程思想，幾何與代數的有機結合形成數形結合思想.這些思想是對數學知識本質的概括和濃縮，而數學方法是數學思想的具體反映，如整體思想中體現了換元法.這些數學思想與方法是數學學習的精髓，是解題的金鑰匙.在解題教學中回歸數學思想與方法的滲透，是提升學生解題能力的關鍵，也是培養能力、發展思維的重要途徑，甚至影響著學生以后的數學學習與知識的應用能力.

例3 反比例函數y=k/x（x＞0）過點A（3，4），直線AC與x軸交于點C（6，0），過點C作x軸的垂線BC交反比例函數圖象于點B.

（1）求k的值與點B的坐標；

（2）在平面內有點D，使得以A，B，C，D四點為頂點的四邊形為平行四邊形，試寫出符合條件的所有點D的坐標.

分析：第（1）問以函數思想來指導解題，具體體現在用待定系數法求k的值，求出k=12，點B的坐標是（6，2）.

第（2）問，若以A，B，C，D四點為頂點的四邊形為平行四邊形，則需在已知A（3，4），B（6，2），C（6，0）的前提下求點D.由于平行四邊形的形狀具有不確定性，因此需要分類討論，所以以分類討論思想為指導來解題.

不妨以AC為平行四邊形的邊還是對角線為分類標準進行分類討論.

①當AC為對角線時，如圖5，AD∥BC，且AD=BC，建立關系，列方程y_A-y_D=y_B-y_C，求得D（3，2）.

②當AC為一邊時，如圖5，當四邊形ACBD′為平行四邊形時，AD′∥CB且AD′=CB.

建立關系，列方程y_D′-y_A=y_B-y_C，求得點D′（3，6）.

③當AC為一邊時，如圖5，當四邊形ACD″B為平行四邊形時，AC=BD″且AC=BD″.

建立關系，列方程x_D″-x_B=x_C-x_A，y_D″-y_B=y_C-y_A，求得D″（9，-2）.

綜上所述，符合條件的點D的坐標是（3，2）或（3，6）或（9，-2）.

這是一道反比例函數與平行四邊形的綜合題，以此題為載體，在講解時以函數思想、方程思想和分類討論思想、數形結合思想為統領，指導學生如何一步步運用所學數學知識解題.在融會貫通平行四邊形的性質、判定等知識的同時，也讓學生理解蘊含在其中的思想方法，以及思想方法對解題的指導作用.

九年級的復習資料堆積如山，唯有把握其中的數學本質，才能把資料從厚變薄，把所學的知識系統化、條理化.九年級的題型千變萬化，題設條件錯綜復雜，唯有緊扣數學的本質，才能隨機應變，輕松應對.回歸定義、基本原型、數學思想與方法正是回歸數學本質的具體方法.這種由表及里、循序漸進、步步深入的解題方式，能幫助學生尋覓到解題的門道，尋求到通解與通法，以不變應萬變，從而脫離茫茫題海，體驗成功解題的樂趣，實現數學能力的有效提升，也無形中增強了學生備戰中考的信心.