妙解一道等腰三角形背景下的判斷形狀問題

孟祥云

【摘要】等腰三角形是初中幾何問題中的一個重要三角形之一.解決等腰三角形問題有兩大思路：一是證明三角形的兩個腰相等，二是證明三角形中的兩個內角相等.本文介紹一道等腰三角形背景下的判斷形狀問題的幾種解法，以供讀者參考.

【關鍵詞】等腰三角形；初中數學；解題技巧

對于等腰三角形背景下的判斷形狀問題，一般來說，需要判斷的三角形的形狀都是等腰三角形，也有可能是特殊的等腰三角形如等腰直角三角形、等邊三角形等.在解答此類問題時要抓住等腰三角形問題的兩大思路，尋找相同的角或者邊，即可求解.以下是一道典型例題的四種解法.

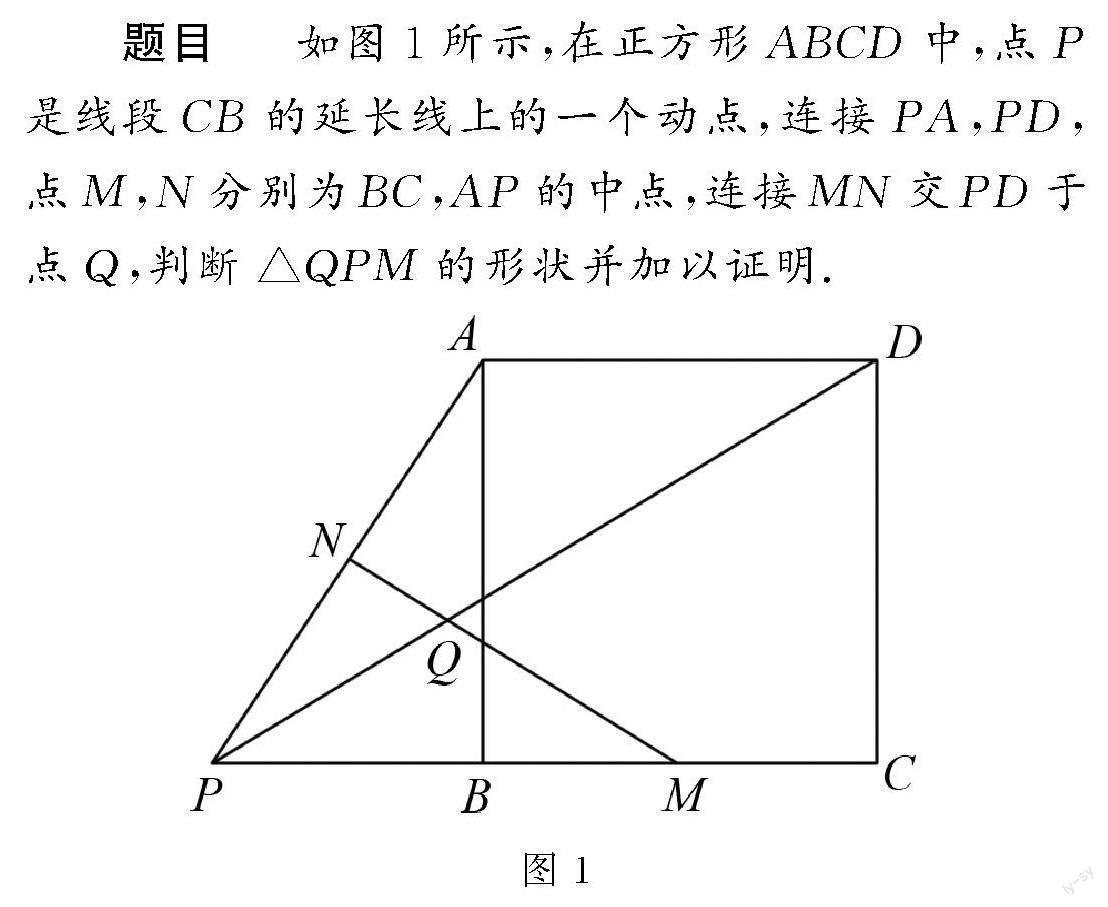
題目 ??如圖1所示，在正方形ABCD中，點P是線段CB的延長線上的一個動點，連接PA，PD，點M，N分別為BC，AP的中點，連接MN交PD于點Q，判斷△QPM的形狀并加以證明.

圖1

問題分析? 對于此類判斷形狀的問題，在解題前可以先觀察題目所給的圖形大致判斷形狀，此題不難看出△QPM是等腰三角形.之后，以此結論為出發點，理清證明思路，在此過程中可充分利用全等或者相似三角形來得到角或者邊相等的結論.

解法1? 如圖2所示，延長BC至點E，使CE=BP，連接AE.

因為PB=CE，

所以PB+BC=CE+BC，即CP=BE.

因為四邊形ABCD是正方形，

所以AB=DC，∠ABC=∠DCB=90°.

在△DCP和△ABE中，DC=AB，

∠DCP=∠ABE，CP=BE，

所以△DCP≌△ABE，故∠1=∠E.

因為點M為BC的中點，

所以MB=MC，MB+BP=MC+CE，

即MP=ME，

所以M為PE的中點.

因為N是AP的中點，

所以NM∥AE，

所以∠2=∠E，所以∠1=∠2，QP=QM，

所以△QPM是等腰三角形.

解法2? 如圖3所示，延長MN交DA的延長線于點E.

過點M作MF⊥AD于點F，則∠AFM=90°.

因為四邊形ABCD是正方形，

則∠ABC=∠BCD=∠CDA=∠DAB=90°，

所以四邊形ABMF，四邊形FMCD均是矩形，

所以AB=FM=DC，AF=BM，FD=MC.

因為點M，N分別為BC，AP的中點，

所以MB=MC，AN=PN，AF=MC.

因為四邊形ABCD是正方形，

所以AD∥BC.

所以∠E=∠NMP，

∠EAN=∠MPN，

所以△AEN≌△PMN，

則AE=PM，

所以AE+AF=PM+MC，

即EF=PC，

所以tan∠E=FMEF，tan∠DPC=DCPC，

所以∠E=∠DPC=∠NMP，

則QP=QM，

所以△QPM是等腰三角形.

解法3? 如圖4所示，過點N作NH⊥PM于點H，

則∠NHM=90°.

因為點M，N分別為BC，AP的中點，

所以MB=12BC，PN=12PA.

因為四邊形ABCD是正方形，

所以∠ABC=∠BCD=90°，AB=CD.

因為∠NHM=∠ABC=90°，

所以NH∥AB，

則NHAB=PNPA=PHPB=12，

所以NH=12AB=12CD，BH=12PB，

HM=BH+MB=12PB+12BC=12PC.

在Rt△NHM中，tan∠QMP=NHHM=CDPC.

在Rt△PCD中，tan∠QPM=CDPC，

所以∠QMP=∠QPM，QP=QM，所以△QPM是等腰三角形.

解法4? 如圖5所示，取AD的中點E，連接NE，NB，

則AE=12AD.

因為四邊形ABCD是正方形，

所以∠ABC=∠BAD=90°，

AD∥BC，AD=BC，

則∠ABP=90°，∠ADP=∠DPC.

因為點M為BC的中點，

所以BM=12BC.

因為AD=BC，

所以AE=BM.

因為點N，E分別為AP，AD的中點，

所以NE∥PD.

因為在Rt△ABP中，點N為AP的中點，

所以NB=12AP=NP=NA，

則∠NAB=∠NBA，∠NAE=∠NBM.

在△NAE和△NBM中，

NA=NB，∠NAE=∠NBM，AE=BM，

所以△NAE≌△NBM，

則∠AEN=∠BMN.

又因為NE∥PD，

所以∠AEN=∠ADP=∠DPC，

則∠BMN=∠DPC，

所以QP=QM，

故△QPM是等腰三角形.

結語

證明等腰三角形，除了常用的“等邊對等角”，還可以使用相似或者全等三角形，計算兩角的三角函數值等結論.需要注意的是，對于此類問題種比較復雜的情況，一般不會給出直接的條件，有時需要學生能夠靈活構造出全等三角形，或者通過延長或者旋轉的方法來得到所需條件.