刪繁就簡(jiǎn)三秋樹(shù)，領(lǐng)異標(biāo)新二月花

王浩宇

摘要：分析2023年數(shù)學(xué)新高考Ⅰ卷，發(fā)現(xiàn)題型和難度相對(duì)穩(wěn)定.新高考試題簡(jiǎn)潔明了，考查學(xué)生基礎(chǔ)知識(shí)的同時(shí)重視學(xué)生關(guān)鍵能力的探求.本文中通過(guò)整體試卷評(píng)析、部分試題評(píng)析及近三年全國(guó)卷對(duì)比評(píng)析三個(gè)板塊對(duì)2023年新高考Ⅰ卷進(jìn)行評(píng)價(jià).

關(guān)鍵詞：新高考Ⅰ卷；試題分析；試卷評(píng)析

1 綜述

2023年教學(xué)新高考Ⅰ卷嚴(yán)格依據(jù)高中課程和高中課程評(píng)價(jià)體系，深化基礎(chǔ)性和綜合性，注重?cái)?shù)學(xué)運(yùn)算［1］.試題簡(jiǎn)潔明了，體現(xiàn)數(shù)學(xué)的簡(jiǎn)潔美，考查基礎(chǔ)知識(shí)的同時(shí)重視學(xué)生關(guān)鍵能力的探求，傳承經(jīng)典的同時(shí)又體現(xiàn)了對(duì)考生的人文關(guān)懷，開(kāi)拓創(chuàng)新，服務(wù)于高校人才選拔.

2 整體試卷評(píng)析

2.1 難度適中，梯度設(shè)置合理

今年新高考Ⅰ卷整體難度與去年基本持平，試題著力于通性通法和綜合能力的考查.具體考點(diǎn)分布情況如表1：

試卷簡(jiǎn)單題共60分，體現(xiàn)新高考Ⅰ卷植根教材、重視基礎(chǔ)、啟發(fā)課堂德育的理念.對(duì)比去年試題，選擇題難度略降，填空題難度相當(dāng)；中等難度題有一定計(jì)算量，需要綜合運(yùn)用所學(xué)知識(shí)求解；層次高的難題，大約占29分，試題重視思維的創(chuàng)新和學(xué)生的綜合能力，考查邏輯推理、數(shù)據(jù)分析、數(shù)學(xué)運(yùn)算等核心素養(yǎng).

2.2 層次分明，突出重點(diǎn)內(nèi)容

2023年新高考Ⅰ卷在多方面體現(xiàn)重點(diǎn)內(nèi)容重點(diǎn)考，具體內(nèi)容如圖2所示：

相比浙江卷，新高考Ⅰ卷增加了多選題，豐富題目類型的同時(shí)注重知識(shí)點(diǎn)的覆蓋，突出主干知識(shí).其中函數(shù)與導(dǎo)數(shù)、概率、立體幾何、圓錐曲線考題較多，集合、復(fù)數(shù)、直線與圓、平面向量更多體現(xiàn)工具性.同時(shí)，今年客觀題難度整體降低，中低檔試題數(shù)量增加，旨在減少學(xué)生“放題”的情況.

2.3 反對(duì)套路，注重全面發(fā)展

新高考Ⅰ卷未劃定試卷結(jié)構(gòu)，例如今年導(dǎo)數(shù)位于第三題.解答題從第二小題開(kāi)始，每題均能多解，這是新高考在引導(dǎo)學(xué)生做“六邊形戰(zhàn)士”.以解三角形為例，今年考查求三角形的高，相比去年考查正弦定理、余弦定理與兩角和差的正余弦公式，三角形高的求解更能展現(xiàn)學(xué)生對(duì)三角形本質(zhì)的理解，體現(xiàn)了新高考的反套路.

新高考還在選擇題中反套路，每年選擇題答案中ABCD數(shù)量都不同，加大了考生猜題的難度.

2.4 追根溯源，回歸書本題源

2023年新高考Ⅰ卷選擇題起點(diǎn)較低，許多題目源自書本.雖然試題來(lái)源于課本，但又高于課本，簡(jiǎn)單的題目中也有“繞彎”的內(nèi)容.具體內(nèi)容如表2：

例如試卷第7題，以選擇性必修二人教A版課后習(xí)題第7題第一小題為題源，借助充分條件與必要條件的工具性，考查學(xué)生對(duì)數(shù)列定性分析的掌握情況，以概念、定理、試題為命題的起點(diǎn)，注重“四基”的考查.2021年全國(guó)甲卷第7題也屬于類似題目.上述題目讓學(xué)生感悟定性分析的同時(shí)培育了邏輯推理的數(shù)學(xué)能力，體現(xiàn)了數(shù)學(xué)的育人價(jià)值.

[HJ1.35mm]

2.5 簡(jiǎn)潔明了，彰顯數(shù)學(xué)之美

希爾伯特在《數(shù)學(xué)問(wèn)題》中曾說(shuō)過(guò)：“一個(gè)數(shù)學(xué)理論，只有當(dāng)你能把它向你在街上遇到的第一人闡述得很清楚時(shí)，它才算完整.”新高考Ⅰ卷在各個(gè)方面均體現(xiàn)了簡(jiǎn)潔美.具體內(nèi)容如圖3：

此類題目共計(jì)32分，說(shuō)明依賴題海在高考中并不是有效的.知識(shí)的綜合讓題目思維量更大，考查學(xué)生是否真正掌握了相關(guān)概念.

3 部分經(jīng)典題型與創(chuàng)新題型評(píng)析

3.1 講究算理，計(jì)算需謹(jǐn)慎

運(yùn)算是高考重點(diǎn)考查內(nèi)容之一，主要分為運(yùn)算規(guī)則、運(yùn)算律、運(yùn)算方法的考查.

第10題屬于應(yīng)用題，主要考查學(xué)生對(duì)對(duì)數(shù)和不等式運(yùn)算性質(zhì)的熟練程度.

（2023年新高考Ⅰ卷·10）噪聲污染問(wèn)題越來(lái)越受到重視.用聲壓級(jí)來(lái)度量聲音的強(qiáng)弱，定義聲壓級(jí)Lp=20×lgpp0，其中常數(shù)p0（p0>0）是聽(tīng)覺(jué)下限閾值，p是實(shí)際聲壓.下表4為不同聲源的聲壓級(jí)：

評(píng)析：本題以時(shí)事熱點(diǎn)新能源汽車為背景，設(shè)置科學(xué)研究情境，體現(xiàn)數(shù)學(xué)的生活性.此類問(wèn)題求解時(shí)要牢牢抓住中間量，將其余變量用中間量來(lái)表示.相比前幾年的比大小試題，結(jié)合實(shí)際情境更能培養(yǎng)學(xué)生閱讀能力和數(shù)學(xué)算理.

評(píng)析：掌握運(yùn)算規(guī)則可以拓寬解題思路.以第11題抽象函數(shù)為例，基本策略是根據(jù)抽象函數(shù)的結(jié)構(gòu)構(gòu)造函數(shù)求解.基于g（xy）=g（x）+g（y）中乘法變加法的運(yùn)算規(guī)則，以對(duì)數(shù)函數(shù)為基礎(chǔ)構(gòu)造函數(shù)求解.常見(jiàn)的運(yùn)算規(guī)則還有指數(shù)冪運(yùn)算規(guī)則、三角函數(shù)運(yùn)算規(guī)則等.

〔2023年新高考Ⅰ卷·20（2）〕設(shè)等差數(shù)列{an}的公差為d，且d>1.令bn=n2+nan，記Sn，Tn分別為數(shù)列{an}，{bn}的前n項(xiàng)和.

若{bn}為等差數(shù)列，且S99－T99=99，求d.

評(píng)析：合適的運(yùn)算方法可以讓解題思路更清晰.例如數(shù)列第二小題以常規(guī)方法求解對(duì)思維含量要求較高，若以b1，b2，b3間的關(guān)系求解能最快得出結(jié)果，體現(xiàn)運(yùn)算方法選擇的重要性.

歷年高考計(jì)算都是重中之重，以考促教，為教師教學(xué)提供方向.此題對(duì)深諳算理的考生不成問(wèn)題，但對(duì)不夠細(xì)心認(rèn)真的學(xué)生則是一個(gè)“暗點(diǎn)”，考查了學(xué)生數(shù)學(xué)運(yùn)算等核心素養(yǎng).如果學(xué)生心理素質(zhì)較好，能夠合理選擇算法此題甚至能成為簡(jiǎn)單題，這也說(shuō)明平時(shí)培養(yǎng)學(xué)生算理的重要性［2］.

3.2 結(jié)合模型，初判對(duì)與錯(cuò)

（2023年新高考Ⅰ卷·12）下列物體中，能夠被整體放入棱長(zhǎng)為1（單位：m）的正方體容器（容器壁厚度忽略不計(jì)）內(nèi)的有（??）.

A.直徑為0.99 m的球體

B.所有棱長(zhǎng)均為1.4 m的四面體

C.底面直徑為0.01 m，高為1.8 m的圓柱

D.底面直徑為1.2 m，高為0.01 m的圓柱體

評(píng)析：立體幾何的接切問(wèn)題一般考查外接球和內(nèi)切球，但本題考查正方體的接切問(wèn)題，四個(gè)選項(xiàng)難度逐漸增加，分別考查球、正四面體、圓柱三種空間幾何體，考查范圍更廣，更能表現(xiàn)考生思維的靈活性與創(chuàng)造性.

此類題目解題步驟為：套用已知模型→比較已知模型與選項(xiàng)差異→極限法求解問(wèn)題.解題時(shí)，需要學(xué)生充分發(fā)揮空間想象能力.基于此，在教學(xué)過(guò)程中，教師可以結(jié)合書本和課標(biāo)中的立體幾何模型授課，幫助學(xué)生熟悉常見(jiàn)模型的同時(shí)培養(yǎng)學(xué)生空間想象能力.

3.3 閱讀分析，課外需拓展

（2023年新高考Ⅰ卷·21）甲、乙兩人投籃，每次由其中一人投籃，規(guī)則如下：若命中則此人繼續(xù)投籃，若末命中則換為對(duì)方投籃.無(wú)論之前投籃情況如何，甲每次投籃的命中率均為0.6，乙每次投籃的命中率均為0.8.由抽簽確定第1次投籃的人選，第1次投籃的人是甲、乙的概率各為0.5.

（1）求第2次投籃的人是乙的概率；

（2）求第i次投籃的人是甲的概率；

（3）已知：若隨機(jī)變量Xi服從兩點(diǎn)分布，且P（Xi=1）=1－P（Xi=0）=qi，i=1，2，……，n，則E（∑ni=1Xi）=∑ni=1qi.記前n次（即從第1次到第n次投籃）中甲投籃的次數(shù)為Y，求E（Y）.

評(píng)析：第21題第（1）問(wèn)以選擇性必修三（人教A版）7.1.2中的思考題為題源，考查全概率公式，求解時(shí)需要仔細(xì)讀題，分清主從關(guān)系，借助對(duì)應(yīng)模型求解.

第（2）（3）問(wèn)則以選擇性必修三課后復(fù)習(xí)參考題第10題（第91頁(yè)）為題源，考查學(xué)生對(duì)概率與數(shù)列的掌握情況與獲取信息的能力，把問(wèn)題轉(zhuǎn)化為數(shù)列模型.以前應(yīng)用類考題以函數(shù)與方程為主，本題則以馬爾科夫鏈為背景，取材于學(xué)生熟悉的情境，考查學(xué)生多知識(shí)綜合運(yùn)用的能力，為大學(xué)學(xué)習(xí)做鋪墊，發(fā)揮高考的選拔功能.相比傳統(tǒng)的概率考題卡方檢驗(yàn)、線性回歸等，基于統(tǒng)計(jì)模型的試題更為靈活.相關(guān)模型還有決策樹(shù)、樸素貝葉斯、邏輯回歸、線性回歸等，可以作為出題的參考內(nèi)容.此類題目在2019年全國(guó)乙卷中也曾出現(xiàn)過(guò).

3.4 模式改變，不變應(yīng)萬(wàn)變

（2023年新高考Ⅰ卷·22）在直角坐標(biāo)系xOy中，點(diǎn)P到x軸的距離等于點(diǎn)P到點(diǎn)0，12的距離，記動(dòng)點(diǎn)P的軌跡為W.

（1）求W的方程；

（2）已知矩形ABCD有三個(gè)頂點(diǎn)在W上，證明：矩形ABCD的周長(zhǎng)大于33.

評(píng)析：與前幾年導(dǎo)數(shù)壓軸題不同，今年的壓軸題是解析幾何，題目由易到難，第（1）小題入口較寬，根據(jù)題意列式求解即可.但學(xué)生面對(duì)壓軸題時(shí)，常常會(huì)產(chǎn)生畏懼心理，導(dǎo)致失分.這需要教師在平時(shí)多鼓勵(lì)學(xué)生勤于思考、勇于探索，不能看到壓軸題就畏難、放棄，體現(xiàn)了命題人的良苦用心和數(shù)學(xué)的育人價(jià)值觀.

第（2）小題較為復(fù)雜，是拉開(kāi)學(xué)生分?jǐn)?shù)差距的點(diǎn).本小題可以從矩形的鄰邊垂直切入，通過(guò)設(shè)點(diǎn)或設(shè)線求解問(wèn)題.但不管用哪種方法，都需要回歸直線的斜率，讓問(wèn)題變得更直觀，這是本題設(shè)計(jì)的亮點(diǎn).題目本身并不復(fù)雜，條件清晰，解題時(shí)學(xué)生能輕松想到兩點(diǎn)之間的距離公式（x1－x2）2+（y1－y2）2以及弦長(zhǎng)公式1+k2＼5|x1－x2|，但計(jì)算仍是學(xué)生的痛點(diǎn)，需要選擇合適的算理.本題主要考查數(shù)學(xué)運(yùn)算、邏輯推理等核心素養(yǎng)，同時(shí)對(duì)學(xué)生的心理素質(zhì)、應(yīng)變能力提出了一定的要求.

解析幾何大題對(duì)廣大考生來(lái)說(shuō)是一個(gè)挑戰(zhàn)，要求學(xué)生對(duì)通性通法能熟練應(yīng)用的同時(shí)，還需思維靈活、注重算理，屬于層次較高的難題.因此在復(fù)習(xí)中要引導(dǎo)學(xué)生合理猜想，結(jié)合算理發(fā)掘關(guān)鍵點(diǎn)，突破關(guān)鍵，計(jì)算到底，從而提升數(shù)學(xué)綜合能力與核心素養(yǎng)，盡力做到難題多拿分，簡(jiǎn)單題不失分.

4 總結(jié)：靈活考查，復(fù)習(xí)需要方向.

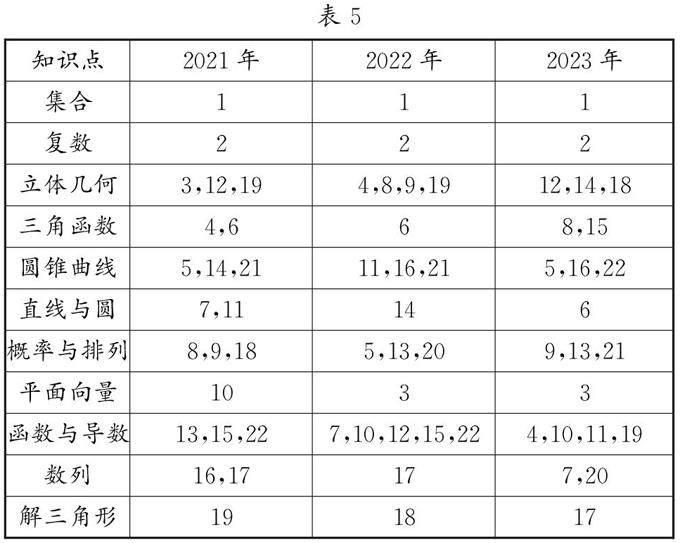
2023年新高考Ⅰ卷為后續(xù)高考提供了復(fù)習(xí)方向與教學(xué)思路，雖然每年考題難度、位置分布不同，但作為浙江參與新高考的第一年，題型改變?nèi)杂幸欢ㄒ?guī)律，以下（表5）是2021年-2023年新高考Ⅰ卷考查的知識(shí)點(diǎn)位置分布情況.

歷年高考試卷中有變與不變兩部分.其中，①函數(shù)與導(dǎo)數(shù)、立體幾何、圓錐曲線、概率與排列每年均有大量題目，難度跨度較大；②平面向量、直線與圓、解三角形、數(shù)列部分題號(hào)雖有變動(dòng)，但難度適中，題量?jī)H有1到2題；③集合與復(fù)數(shù)等基礎(chǔ)考點(diǎn)的題號(hào)、難度3年內(nèi)均未改動(dòng);④函數(shù)、向量、幾何、統(tǒng)計(jì)、概率、數(shù)列、不等式仍是高考的重點(diǎn)與難點(diǎn).解題時(shí)，考生需要把握常用邏輯用語(yǔ)、集合、不等式、函數(shù)與導(dǎo)數(shù)的工具性，多角度思考問(wèn)題.

新高考Ⅰ卷另一特點(diǎn)是中檔題多，這為高考復(fù)習(xí)提供了方向：普通考生需注意在集合、復(fù)數(shù)、平面向量等簡(jiǎn)單題上不丟分，在直線與圓、三角函數(shù)、解三角形、立體幾何、數(shù)列等中檔題上多拿分.想拿高分的考生也需注意，雖然考查的知識(shí)難度年年發(fā)生變化，但不存在遺漏的考點(diǎn)，這是高考在傳達(dá)“不放棄任意一個(gè)知識(shí)點(diǎn)”的觀念.

對(duì)比2021年-2023年新高考試題發(fā)現(xiàn)：數(shù)列大題在2021年難度較大，但2022和2023年處于中檔難度.2023年三角函數(shù)大題的難度有一定提高，函數(shù)與導(dǎo)數(shù)的難度有所降低.近幾年新高考小題中都出現(xiàn)了與導(dǎo)數(shù)相關(guān)的題目，旨在打破傳統(tǒng)印象中導(dǎo)數(shù)均是難題的觀念，立足計(jì)算，考查導(dǎo)數(shù)的工具性，后續(xù)是否繼續(xù)降低難度仍需觀察.另外，每年新高考都在應(yīng)用題中進(jìn)行創(chuàng)新，其中2023年新高考Ⅰ卷應(yīng)用題具體內(nèi)容如表6所示.

在命題原則上，新高考Ⅰ卷注重以下三點(diǎn)：

（1）跳出框架.新高考并不存在固定題型，規(guī)避題型模式化和解題模式化，但也提供了復(fù)習(xí)的方向和策略.在此對(duì)2024年新高考?jí)狠S題進(jìn)行預(yù)測(cè)：能作為壓軸題出現(xiàn)的往往有數(shù)列、導(dǎo)數(shù)、解析幾何，新高考以數(shù)列壓軸的可能性較低，2023年是圓錐曲線壓軸，故考慮2024年有可能回歸導(dǎo)數(shù)壓軸，考法可能會(huì)參照2023年，結(jié)合高等數(shù)學(xué)中的重要結(jié)論呈現(xiàn)問(wèn)題會(huì)更簡(jiǎn)潔.

（2）注重計(jì)算.新高考題目計(jì)算量很大，故需要注重算理，掌握算法，計(jì)算到底.

（3）注重應(yīng)用.新高考題目往往結(jié)合其他知識(shí)或加入實(shí)際情境，對(duì)基礎(chǔ)知識(shí)進(jìn)行深化，將題目改編成需要“繞彎”的難題.考試時(shí)，雖然題目給學(xué)生似曾相識(shí)的感覺(jué)，但拿滿分往往較困難.

綜合命題原則與新高考試題特點(diǎn)，總結(jié)出以下三點(diǎn)教學(xué)啟發(fā)：

（1）基于課標(biāo)，牢固掌握知識(shí)

課標(biāo)是出題的依據(jù)，教學(xué)時(shí)基于課標(biāo)設(shè)計(jì)教學(xué)內(nèi)容，讓學(xué)生完全掌握相關(guān)概念，回歸課本，講解通性通法，減少“二級(jí)結(jié)論”.

（2）側(cè)重算理，掌握做題技巧

新高考Ⅰ卷的計(jì)算量較大，因?yàn)橛?jì)算失分較為可惜，因此，平時(shí)要讓學(xué)生自己動(dòng)手運(yùn)算，合理簡(jiǎn)化運(yùn)算，減少運(yùn)算量，培養(yǎng)學(xué)生的運(yùn)算能力，同時(shí)培養(yǎng)學(xué)生運(yùn)用排除法、特殊值法等運(yùn)算技巧解題的能力，提高做題效率.

（3）綜合應(yīng)用，參考課標(biāo)實(shí)踐活動(dòng)

新高考Ⅰ卷的難題會(huì)綜合考查多種知識(shí)點(diǎn)，在平時(shí)教學(xué)過(guò)程中，可以通過(guò)實(shí)踐活動(dòng)幫助學(xué)生完成知識(shí)的整合，避免知識(shí)的碎片化.

參考文獻(xiàn)：

［1］中華人民共和國(guó)教育部.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）[S].北京：人民教育出版社， 2018：1-2.

［2］陳宏.基礎(chǔ)與能力并重 經(jīng)典與創(chuàng)新共存——2022年浙江省高考數(shù)學(xué)試題評(píng)析[J].中學(xué)數(shù)學(xué)，2022（19）：27-32.