高三復習課對新課標推理與證明要求的落實
杜瑛

摘要:數學課堂是由邏輯推理構建起來的,概念的抽象、模型的建立、性質的推導、公式的論證以及問題的演繹,均需邏輯推理素養的支撐.本文中從核心素養和推理與證明的關系、新教材中對推理與證明的教學要求以及新課標高考試題三個角度闡述了新課標對推理與證明的要求,并通過幾個實際教學中的例子,對高三復習課中推理與證明的教學提出了一些建議.
關鍵詞:推理與證明;高三復習課
《普通高中數學課程標準(2017年版2020年修訂)》(以下簡稱“標準”)的課程內容中去掉了“推理與證明”一章,但“標準”對培養學生推理與證明能力的要求沒有降低.從2021年開始,新課標Ⅰ、Ⅱ卷的六道大題中均有不少于三題涉及到了證明.由此可見,我們要特別關注高三復習課中的推理與證明教學及其思想的滲透.
1 推理與證明的要求沒有降低
1.1 數學核心素養和推理與證明的關系
邏輯推理主要表現為:掌握推理的基本形式和規則,發現問題和提出命題,探索和表述論證過程,理解命題體系,有邏輯地表達與交流[1].培養邏輯推理素養是發展推理與證明能力的重要途徑.同時,其他五個核心素養的主要表現均與推理能力有關.由此可見,“標準”對推理與證明的要求沒有降低,而是滲透到了核心素養的內涵之中.
1.2 新教材中對推理與證明教學的要求
摘錄新教材(普通高中教科書數學必修第一冊人教A版)中的三個環節以示例:
(1)(第18頁)思考:例1中命題(1)給出了“四邊形是平行四邊形”的一個充分條件,即“四邊形的兩組對角分別相等”.這樣的充分條件唯一嗎?如果不唯一,那么你能再給出幾個不同的充分條件嗎?
(2)(第46頁)探究:類比等式的基本性質,你能猜想不等式的基本性質,并加以證明嗎?
(3)(第122頁)請你利用對數與指數間的關系證明loga1=0,logaa=1.
新教材圍繞概念、性質和公式的生成設置了“思考”“探究”等活動,這些活動有些需要數學抽象,有些需要邏輯推理,還有些需要論證.它們均指向了推理與證明能力的培養.由此可見,新教材進一步提高了對推理與證明的要求.
1.3 新課標高考卷中的推理與證明問題
摘錄新課標高考考題以示例:
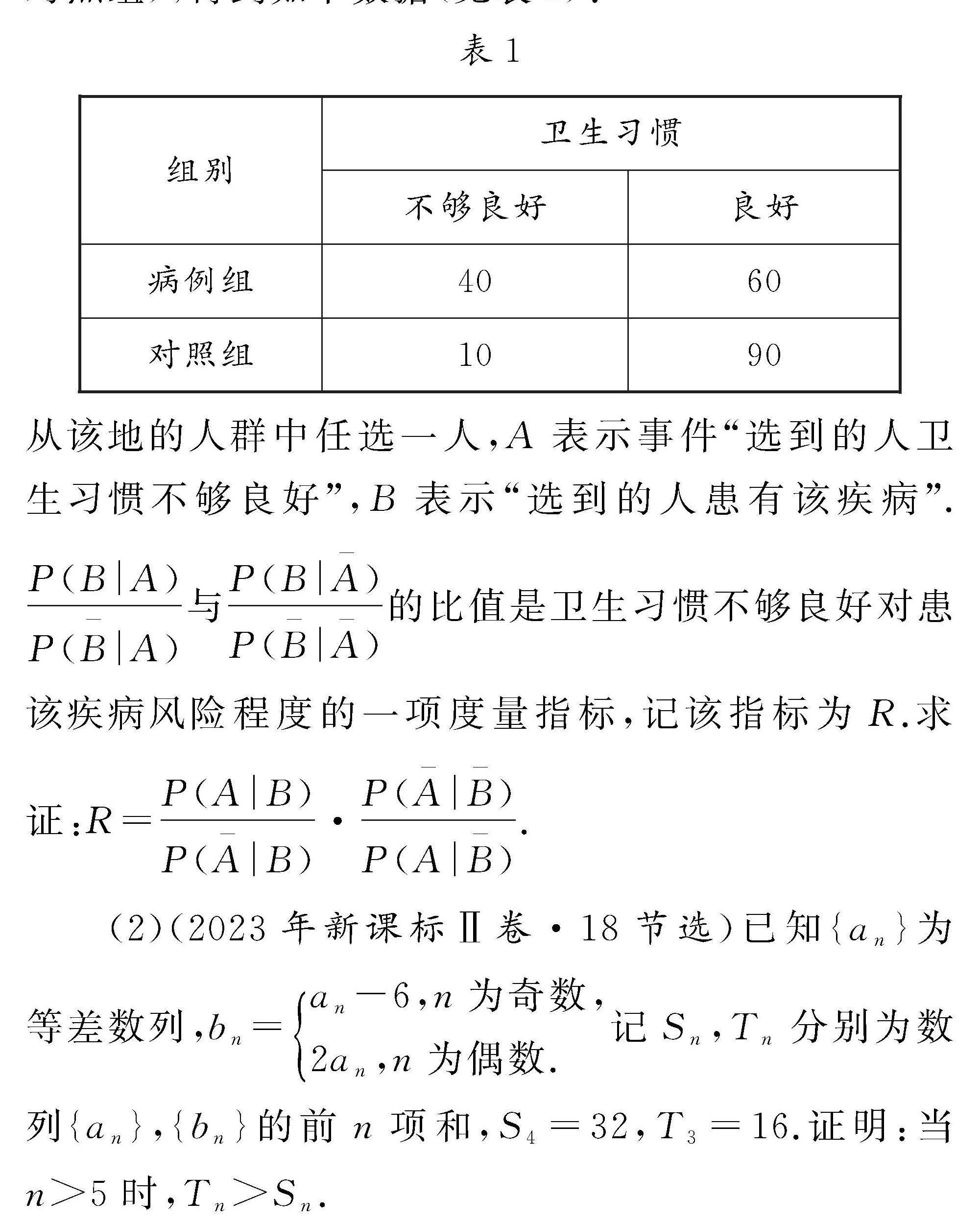
(1)(2022年新課標Ⅰ卷\520節選)一醫療團隊為研究某地的一種地方性疾病與當地居民的衛生習慣(衛生習慣分為良好和不夠良好兩類)的關系,在已患該疾病的病例中隨機調查了100例(稱為病例組),同時在未患該疾病的人群中隨機調查了100人(稱為對照組),得到如下數據(見表1):
表1
組別
衛生習慣
不夠良好
良好
病例組
40
60
對照組
10
90
從該地的人群中任選一人,A表示事件“選到的人衛生習慣不夠良好”,B表示“選到的人患有該疾病”.P(B|A)P(B-|A)與P(B|A-)P(B-|A-)的比值是衛生習慣不夠良好對患該疾病風險程度的一項度量指標,記該指標為R.求證:R=P(A|B)P(A-|B)\5P(A-|B-)P(A|B-).
(2)(2023年新課標Ⅱ卷\518節選)已知{an}為等差數列,bn=an-6,n為奇數,
2an,n為偶數.記Sn,Tn分別為數列{an},{bn}的前n項和,S4=32,T3=16.證明:當n>5時,Tn>Sn.
新高考卷中的推理與證明結合概率、數列、解析幾何、函數與導數等問題,以數學公式推導、數學概念應用、數學結論探究為出發點,綜合考查學生的邏輯推理、數學建構、探索與表述能力.由此可見,新課標高考試題進一步提高了對推理與證明的要求.
2 推理與證明教學的三個關注點
2.1 關注推理與證明意識的培養
數學課堂是由邏輯推理構建起來的,概念的抽象、模型的建立、性質的推導、公式的論證以及問題的演繹,均需邏輯推理素養的支撐.教學中要培養學生有意識地進行推理的能力,如表述“曲線的方程”的概念,論述“f′(x)>0與f(x)單調遞增”之間的關系,推導“不等式的性質”,等等.在解決問題的過程中,讓學生感受定義是嚴謹的、逆命題的真假需要驗證、公式與性質需要證明,進而發展學生的自主推理與論證意識.
2.2 關注充要條件的論證意識
數學定義是充要的,判定定理是充分的,性質定理是必要的.一個真命題的逆命題不一定為真.充要性的研究是培養邏輯推理能力的一個好途徑.課堂中,對數學結論充要性的判斷和有意識的論證,有利于培養學生思維的辯證性和嚴謹性.
2.3 關注推理與證明書寫的規范性
笛卡兒說:“要想獲得真理和知識,惟有兩件武器,那就是清晰的直覺和嚴格的演繹.”將邏輯推理過程完整地書寫出來,就是用數學的語言表達客觀世界.數學表述要嚴謹,推理要有嚴格的依據,前后邏輯關系要清晰.教學中要培養學生書寫的規范性,在書寫的過程中厘清思維的邏輯關系,也是培養推理與證明能力的一個好途徑.
3 高三復習課中培養推理與證明能力的建議
結合上述分析和實際教學經驗,筆者提出高三復習課中培養推理與證明能力的三點建議.
3.1 培養學生口頭論證能力
例1? (2022年天津)“x為整數”是“2x+1為整數”的(? ).
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分又不必要條件
遇到充要條件的判斷問題時,要求學生進行口頭論證,及時糾正論述過程中的不規范處,以幫助學生從正逆兩個方向感受完整的邏輯思維過程,并有邏輯地表達與交流.同時,也有利于培養學生的主動論證意識.
3.2 重視數學公式的推導與證明
例2? 在對人體的脂肪含量和年齡之間的關系的研究中,科研人員獲得了一些年齡和脂肪含量的簡單隨機樣本數據(xi,yi)(i=1,2,……,20,25 參考公式:r=∑ni=1(xi-x-)(yi-y-)? ∑ni=1(xi-x-)2? ∑ni=1(yi-y-)2, =∑ni=1(xi-x-)(yi-y-)∑ni=1(xi-x-)2,=y--x-. 計算r與分別有兩個公式,兩公式之間能夠相互推導.例2中給出的數據與公式不是對應的,需要推導出另一個公式,才能代入數據計算,這就要求我們在課堂中要關注數學公式的推導教學.例如:點到直線距離公式的推導、運用指數的運算性質推導對數的運算性質等.一輪復習課要舍得花時間對重要的公式和結論進行推演,這樣既可加深學生對公式的認識,也能培養學生的推理證明能力. 3.3 重視證明題的教學 例3? (2023年新課標Ⅰ卷\519)已知函數f(x)=a(ex+a)-x. (1)討論f(x)的單調性; (2)證明:當a>0時,f(x)>2ln a+32. 本題綜合考查邏輯推理和數學運算能力、分類討論和化歸思想.第(2)問的解題突破口是結合第(1)問的結論,利用化歸思想,將問題轉化為求證“當a>0時,f(x)min>2ln a+32”,再利用作差比較法求證.證明題對邏輯的嚴密性、思維的統整性和書寫的規范性要求較高,是學生的學習難點,也是考查邏輯推理能力的重要載體.證明能力的培養不是一蹴而就的,需要在教學中逐漸滲透.在高三復習課中,遇到證明問題不能舍棄,要關注邏輯推理的思維教學,關注證明問題的基本思想、方法以及書寫規范的教學. 參考文獻: [1]中華人民共和國教育部.普通高中數學課程標準(2017年版2020年修訂)[S].北京:人民教育出版社,2020.

