一道練習題的深度探究與教學思考

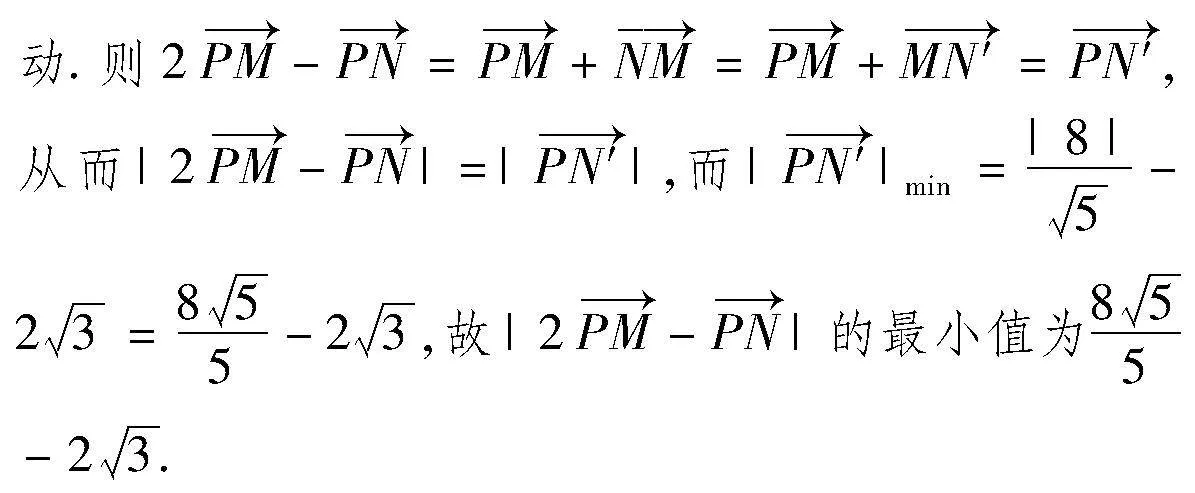
一、習題呈現與分析

試題 （多選）已知圓O：x2+y2=4，直線l：x+y+m=0，則下列結論正確的有（ ）.

A.當m=2時，直線l與圓O相交

D.若直線l上存在點P，圓O上存在兩點A，B，使得∠APB=90°，則m的取值范圍是［－4，4］

有6個未知數，無法構建m的不等式.

面對這樣的兩種原因，筆者也嘗試從幾何與代數兩方面進行探究，以期和大家交流.

二、解法探究

分析1：由于直線l的斜率為定值，要求m的范圍，實際上是求直線l在y軸上的截距的取值范圍.因為點P在直線l上，A，B兩點在圓O上，且使得∠APB=90°.所以從幾何角度考慮，就是要求以圓O上任意兩點A，B為直徑的圓與直線l有公共點即可.由于以圓O上任意兩點A，B為直徑的圓的半徑所屬范圍（0，2］.因此，我們只需要求出其中一個圓，使得直線l與其有公共點且在y軸上的截距取得最值即可.

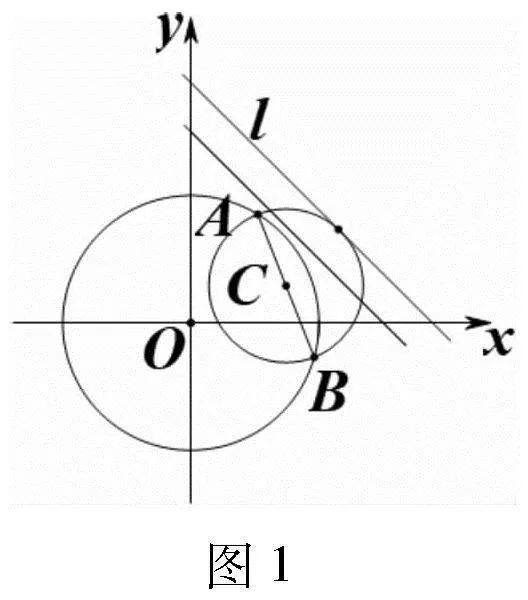
解法1：如圖1，A，B兩點是圓O上任意兩個不同的點，以線段AB為直徑作圓C.對于一個固定的圓C來講，若直線l與圓C相交，則直線l在y軸上的截距取不到最值.因此，只有當直線l與圓C相切時，直線l在y軸上的截距才能取到最值.但是，此時直線l與圓C的切點不一定是離點O最遠的點.所以，我們只需要找到一個圓C，使得該圓上離點O距離最遠的點同時也是直線l與圓C的切點即可.假設以線段AB為直徑的圓C的半徑為r，點M是圓C上離點O最遠的

分析2：從直線l與圓O的位置關系入手.若直線l與圓O相交或相切，則只需要線段AB為圓O的一條直徑就可滿足條件.因此，只需考慮直線l與圓O相離的情形.

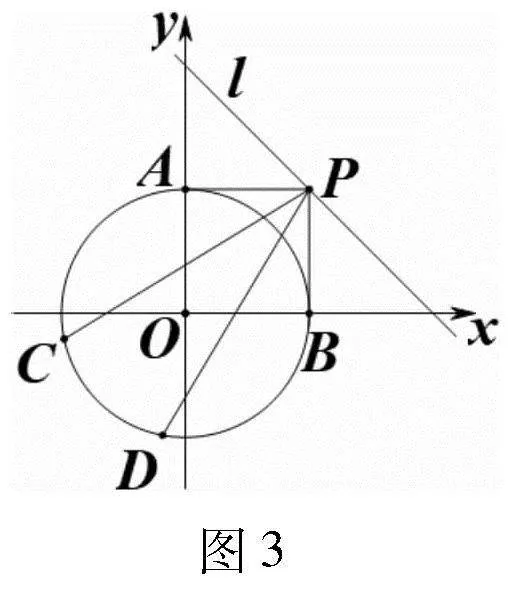
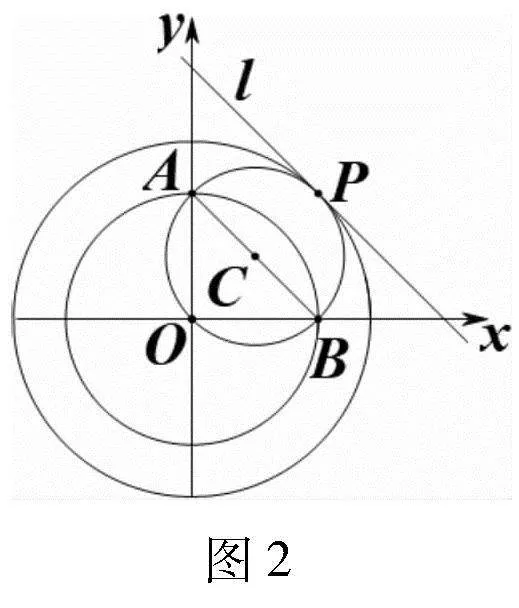
解法2：如圖3，直線PC和PD是圓O的任意兩條割線，直線PA和PB是圓O的兩條切線，從圖可看出，∠CPD≤∠APB.也就是說，若A，B兩點是圓O上任意兩個不同的點，點P是圓O外的任意一點，當且僅當PA和

評注：解法1和解法2都是基于幾何直觀解答.解法1解決了以線段AB為直徑的圓上離點O距離最遠的點的軌跡問題（一般地，設圓O：（x－a）2+（y－b）2=r2（rgt;0），則以圓O的任意弦AB為直徑的圓上的點的軌跡方程為（x－a）2+（y－b）2=2r2），并且利用直線l與此圓相切求出了答案.從該解法中可以看出，問題的關鍵不是直線l上存不存在點P，關鍵在于求出以線段AB為直徑的圓上離點O距離最遠的點的軌跡，只要求出了這個軌跡，直線不管是斜率固定還是截距固定，還是沒有任何特征的直線，都是當直線與這個軌跡相切時取得最值.并且，也可以將直線換成其他的幾何圖形.解法2從直線l與圓O的位置關系入手，先討論了與圓O相交和相切的情形，再討論了相離的情形.另外，從解法2中還獲得了一些額外的知識，如，∠APB取最大值時的幾何條件，進一步的可得解法1中以線段AB為直徑的圓上離點O距離最遠的點的軌跡實際上圓O外一點P作圓O的兩條切線，當兩條切線互相垂直時的點P的軌跡.解法3依靠于解法2，學生之所以沒有順利解決，一個是沒有考慮到臨界時刻，導致方程無法化簡，另一個是對方程有解，不等式有解的處理方法不熟悉.解法3缺失了部分直觀因素，但是對于邏輯推理和數學運算的提升是有幫助的.

三、直接變式

對于本題可從線段的長度，夾角的大小，動點軌跡等角度入手變式.將直線固定，圓的半徑變化，可得：

變式1 設圓O：x2+y2=r2（rgt;0），直線l：x+y+4=0，若直線l上存在點P，圓O上存在兩點A，B，使得∠APB=90°，則r的取值范圍是.

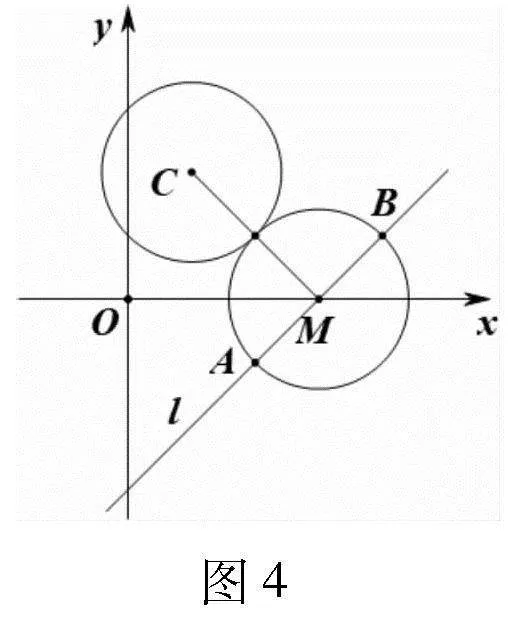
保持圓O不變，將直線換成動圓，可得：

變式2 設圓O：x2+y2=4，圓N：（x－m）2+（y－m）2=4，若圓N上存在點P，圓O上存在兩點A，B，使得∠APB=90°，則m的取值范圍是 .

保持圓O不變，改變直線的幾何特征，可得：

變式3 設圓O：x2+y2=4，直線l：y=k（x－3），若直線l上存在點P，圓O上存在兩點A，B，使得∠APB=90°，則k的取值范圍是 .

讓A，B兩點在直線l上，點P在圓上，可得：

這是線段AB的最小值.隨著A，B兩點在直線上運

保持直線不變，將圓換成橢圓，可得：

當然，也可以將圓換成雙曲線或者拋物線等等，在此不再贅述.通過前面的解法分析，對于本題還可以研究長度，角度，面積，軌跡等問題.下面以長度和角度給出幾個引申變式，以供參考.

四、引申變式

引申1 設圓O：x2+y2=4，直線l：x+y+4=0，點P在直線l，過點P作圓O的兩條切線，切點分別為A，B，求切線長的最小值.

設計意圖：本題意圖在于鞏固學生對切線的掌握，還可以在直線中設置參數，已知切線長的最小值，求參數的值，同時也可設置成求四邊形OAPB的面積最小值問題.

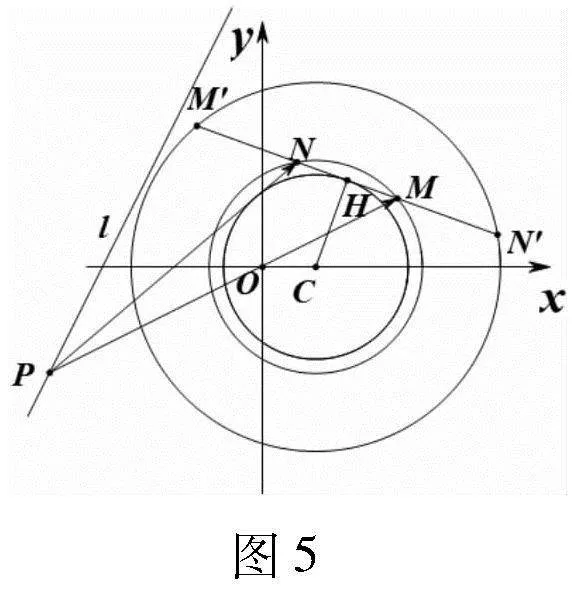
解：由于|MN|=2是定長，故線段MN的中點H在圓（x－1）2+y2=3（從前面的解法1中獲得方法）上運動，如圖5，作M關于N的對稱點M′，N關于M的對稱點N′，則有|M′N|=|MN|=|MN′|=6，且線段M′N′的中點與線段MN的中點H重合.從而M′和N′在圓（x－1）2+y2=12上運

設計意圖：本題的設計一是強化前面解法1中的體現出來的圓內定弦的中點軌跡問題，二是考查向量的轉化以及圓上動點與直線上動點的距離最值問題的求解方法.

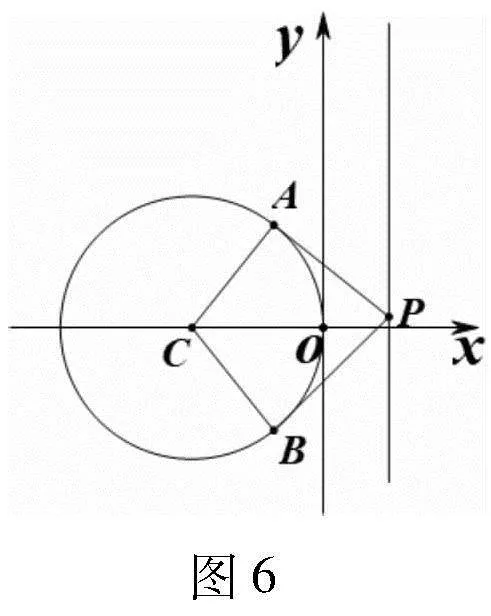
引申3 設P（1，m），圓C：（x+2）2+y2=4，過點P作圓C的兩條切線，切點分別為A，B，求sin∠ACB的最大值.

設計意圖：本題的設置意在強化解法2中的兩條切線張角最大問題.從本題可以看出，當|PC|最小時，∠APB最大，此時∠ACB最小.如果點∠APB沿著直線朝無窮遠處移動時，∠APB在變小，而∠ACB在增大且無限接近于π.可得如下結論：若點P在直線l上運動，當圓心距離P最近時，∠APB最大.此時，圓心與點P的連線垂直于直線l.

五、教學思考

習題評講課是日常教學不可或缺的一個環節，有效的習題評講課有利于發展學生的數學素養，學生在學習解題的過程中“四基”得到鞏固，“四能”得到提高.那么，習題的評講要怎樣才是有效的呢？才是成功的呢？可以肯定的是對答案不加思索，照本宣科肯定不可取，對習題的挖掘只停留在表面也是不可取的.如果學生聽完一道題目的講解，只收獲了該題的答案，而沒有收獲經驗，提高能力，提升素養.那么，這樣的講評是無效的.基于此，筆者嘗試給出下列想法.

5.1 立足學情，精心設計

在講評之前，應當關注學生的答題情況.調查學生試題答錯的原因，弄清到底是學生的能力不足，還是試題本身超出學生的認知水平，亦或者是學生根本就沒認真作答.弄清原因之后，要對癥下藥，精心設計，逐個擊破學生的障礙.

5.2 問題引導，啟發思考

在講評過程中，要設置有啟發性的問題，引導學生思考，開展多種教學活動，盡可能地讓每一位學生都參與進來.對于不同層次的問題應當采取不同的教學方法，借助不同的教學手段.例如，對于抽象程度較高的問題，應當借助數學軟件直觀演示，以化解問題難度.對于試卷中的壓軸題，應當采取合作探究為好，給學生留下思考，交流表達時間.

5.3 積極反思，變式鞏固

在講評結束后，應當要求學生做好解后反思.并將反思以問題鏈的形式給出.如對本文中例題教學的反思問題鏈可考慮：請大家評價一下這幾種方法（從運算量，思維能力，是否容易想到等方面）；從3種解法中還能夠獲得什么（方法是否可以遷移，能不能得出新結論等方面）等等

最后，還要對原題進行改編，以便于學生鞏固學到的知識和經驗.在編制變式題的時既要有知識鞏固型變式，方法遷移運用型變式，也要有問題引申型變式，即橫向變式和縱向變式或橫縱向交叉變式.