談平面幾何教學中立體的優化設計
李洪艷
摘 要:在平面幾何的立體教學中,如何以新課標為指導,充分體現學生的主體地位,是當今教師必須思考的一個問題。因此,在幾何探究式教學中,有必要對標準題進行重新設計。
關鍵詞:平面幾何 例題 重新設計 探究式 再發現 題盡其用
平面幾何教科書中的很多例題因其具有凸顯的典型性、啟發性和代表性而被我們課堂教學所選用。但在例題教學中,僅僅由老師按照原題講,學生聽,展示其解法,難以充分發揮培養學生各項能力的作用。那么如何在新課程標準的指導下,以例題教學為契機,充分體現學生的主體地位,是當今我們必須思考的一個問題。基于此,在幾何探究式教學中,有必要根據學生情況對教科書中的“標準題”進行重新設計,真正做到題盡其用,有效地促成教與學的促進。
今引用教學實踐中對教科書中部分例題的處理方法,談一下幾何例題的重新設計問題。
一、設計“縱向加深型”例題,充分展示學生的再發現過程
案例1
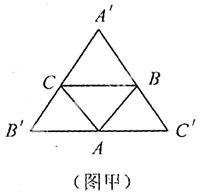
原題:如圖甲,AB∥B′A′,BC∥C′B′,CA∥A′C′,求證:(1)∠ABC=∠B′,∠CAB=∠A′,∠BCA=∠C′。(2)△ABC的頂點分別是△B′C′A′各邊的中點。
重新設計為:已知同原題,(1)觀察圖中有幾個平行四邊形,你是按照什么規律觀察到的?(2)請你作△ABC的高AD所在的直線l1,l1是線段BC的中垂線嗎?為什么?(3)又作△ABC的另外兩條高BE,CF所在的直線l2,l3,你又會發現什么?(4)你能否指出并證明△ABC的三條高有關的一個結論?(5)證明命題“三角形三條高所在的直線共點”。簡要說明你的證明思路。
課后回顧隨想:第(1)問,重在使學生用科學方法認識幾何圖形(任意兩組平行線相交均構成平行四邊形)。糾正不注意發現規律,隨意、隨機觀察圖形的不良習慣,培養學生從組合圖形中分離出基本圖形的空間想象能力。第(2)、(3)、(4)問設計成層次遞增的結論待定型的探究性問題,這些問題自然連貫,比較接近學生的思維發展區。在教師的引導下,大多數學生都有自己的“研究發現”:三角形三條高所在的直線共點。實踐證明,這種“跳一跳再摘到桃子”的做法大大提高了學生的求知欲和幾何問題的意識。問題(5)旨在使學生從整體上掌握本題的思維過程,提高學生的邏輯思維能力和邏輯表達能力。
二、設計“圖形動態化”例題,培養學生的空間想象能力
案例2
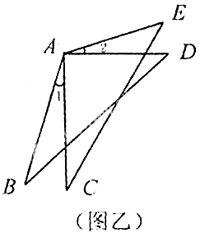
原題:已知:如圖乙,AB=AC,AD=AE,∠1=∠2。求證:△ABD≌△ACE。
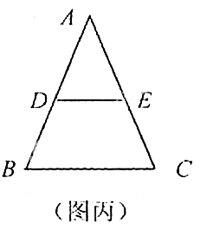
重新設計為:如圖丙,△ABC與△ADE有公共角∠A,AB=AC,AD=AE,(1)線段EC與DB的數量關系是 。(2)今將△ADE繞點A沿“逆時針”方向旋轉,當點E落在△ABC的內部時,畫出圖形,第一問的結論還成立嗎?為什么?(3)在第二問的條件下,△ADE繼續繞點A沿“逆時針”方向旋轉,最終回到原來的位置,在整個旋轉過程中,第一問的結論始終成立嗎?為什么?
課后回顧隨想:第(1)問是簡單問題,給后繼問題的提出做了有益的鋪墊,所以第(2)問的出現馬上使學生進入解題的應激狀態,提高了學生的學習興趣。在這種情景下完成第(2)問的教學,很容易達到原例題所預期的教學效果。第(3)問中所包含的幾種情況的證明雖然與第(1)、(2)兩問的證明區別不大,但這里滲透了幾何變換的數學思想,滲透了分類討論的數學思想,又通過△ADE在旋轉過程中EC與DB的相等關系始終不變,滲透了“動中有靜,變中有不變”的數學辯證觀,從而有效地培養了學生的空間想象能力,使學生形成嚴謹的思維品質成為可能。
三、設計“一題多解型”例題,培養學生的發散思維能力
案例3
原題:畫平行四邊形ABCD,使∠B=45°,AB=2cm,BC=3cm。
課后回顧隨想:幾乎所有的學生首先想到的是課本中的做法,且知道作圖根據是平行四邊形的定義。于是對學生做如下啟發:在此做法中使用了平行四邊形的定義的判定功能,而未使用其性質功能,基于此本題還有無其他解法?同學們躍躍欲試,成功地發現了其他三種解法。我們認為,在例題教學中,題不在多而在精,淺題不“淺”,在淺題面前不淺嘗輒止,是使學生走出題海的誤區,培養學生發散思維能力的必要條件。
四、設計“合情猜想型”例題,提高學生的合情推理能力
案例4
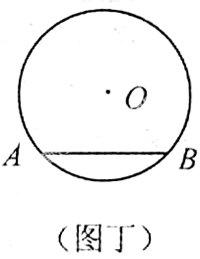
原題:如圖丁,⊙O半徑為13cm,弦AB=24cm,則圓心O到弦AB的距離為 cm。
重新設計為:⊙O的半徑為13cm,弦AB=24cm,動點P從點A出發,沿線段AB向點B運動,點P到達點B后即停止運動。(1)線段OP長度的取值范圍是 。(2)滿足OP為整數的點P的位置共有 個。
課后回顧與隨想:第(1)問完全保持了原題所思考的知識內容,而第(2)問則滲透了用合情猜想解決問題的方法,合情推理是新課標考察的與邏輯推理并重的推理方法之一。在本例的教學中,可使學生深切體會和默認在點P的運動過程中,OP的長度是在5≤OP≤13的范圍內連續變化的。正是由于對這種“連續變化”的、令人耳目一新的思考,使學生打破了邏輯推理的禁錮,體會到了合情推理在解決問題中不可低估的作用,同時促使學生在解決相關問題時,不把合情推理這種順情入理的思維方式拒之門外,大大增強了學生合理選擇推理方法的意識,可有效地促成學生形成良好的思維品質。
五、設計“閱讀型”例題,提高學生的自學能力
這類題一般由教師自行設計,通過閱讀能揭示解題思想方法的課外資料或教師設計的短文,使學生解答與之有關的復雜問題。教學實踐證明,在學生有一定的知識存儲的情況下,解決一些復雜問題時,采用“學生先練習,有困難讀資料,教師點評”這種以學生活動為主的教學方法的效果大大優于“老師講,學生聽”的效果。因此,“閱讀型”例題的設計和運用為提高學生的自學能力、培養學生的自學意識提供了保障,也充分體現了發現法教學的要求和師生角色的轉化。
總之,幾何例題的教學設計是一個復雜而富有藝術性的工作。但毋庸置疑,從培養學生的能力角度出發,必須進行幾何立體的優化設計。作為教師,如果能在新教學理念的指導下,以例題教學為突破點使學生步入幾何殿堂的大門,則足以證明新的教學理念給我們帶來了無窮的教學智慧。
工作單位:河北省昌黎縣赤洋口初級中學

