談小學計算教學中數學基本思想的理解與落實

胡曉敏

【摘要】 《義務教育數學課程標準（2011版）》提出“四基目標”，而作為小學數學最主要內容的計算教學，蘊含著豐富且能讓學生體會的數學基本思想. 在具體教學中，應該依據“有用”來選擇落實何種的基本思想，并把“滲透”作為落實的主要方式，最后通過“持續”滲透保證基本思想的有效落實.

【關鍵詞】 數學基本思想；計算教學；理解；落實

《義務教育數學課程標準（2011版）》明確提出“通過義務教育階段的數學學習，學生能獲得適應社會生活和進一步發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗”的四基目標. 因此，教師教學不僅要讓學生理解和掌握基本數學知識與技能，而且還要讓他們體會與運用數學思想與方法，獲得基本的數學經驗. 本文將以小學計算教學為例，談談如何理解計算教學中的數學基本思想，以及怎樣處理才能將其凸顯和落實.

一、在計算教學中的數學基本思想

計算教學是小學數學教學的主要內容，一直以來，我們比較重視數學思想方法，如數形結合思想、轉化思想、符號化思想等. 數學的基本思想，在本質上有數學抽象、數學推理和數學模型三種思想. 因此，我們有必要厘清基本思想與計算教學中有關思想方法的關系.

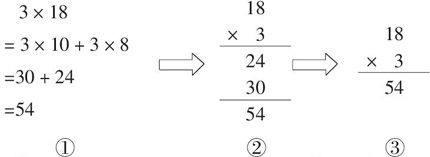
一般來說，計算教學中從情境到數學中的運算法則的產生過程中蘊含著抽象思想，運算法則的提煉中則蘊含著推理思想，而運算法則的應用過程中主要蘊含著建模思想. 如兩位數乘一位數的筆算：

算式①把3 × 18看成3 × （10 + 8）是依據乘法意義的推理而成；比較橫式① 與豎式② 的關系，并最后統一為豎式③，經歷了一個抽象的過程；最后，用獲得列豎式的方法進行練習和運算，則是建立和鞏固列豎式計算的模型. 同時，也說明不同的環節或同樣的環節不同的教學內容，都有可能蘊含著一種或多種數學基本思想.

二、落實數學基本思想的計算教學

上述的分析，已經能比較好地讓我們理解計算教學中數學基本思想的特點. 那么，在具體的計算教學中應該選擇落實何種基本思想？如何落實并確保有效呢？

1. “有用”——落實的首要選擇

數學基本思想依附和體現在教學過程中，不同的內容，或者相同內容不同的階段都蘊含著多元的數學思想. 那么，應該首先去落實何種的基本思想呢？教學論告訴我們，教學目標是教學活動實施的方向和預期達成的結果，是一切教學活動的出發點和最終歸宿. 理所當然，作為教學任務一部分的數學基本思想應該為學生學習服務，與教學內容緊密結合，與課程的學習目標一致. 在教學設計與實施中，應該以“有用”為選擇標準，切勿“求全”. 即選擇能幫助學生掌握知識，實現教學目標，提升數學思維能力的數學思想，讓知識技能的學習與數學思想滲透融為一體，自然貼切. 如人教版五年級上冊第21頁“一個數除以小數”的例5（如圖1）：

圖 1

當引導學生探究7.65 ÷ 0.85的算法時，既可以將米的單位轉化成厘米，將除數變成整數，也可利用“商不變性質”進行轉化. 最后，引導學生歸納出除數是小數的除法運算法則. 這個過程中，雖然蘊含有抽象思想、模型思想，但對獲得除數是小數的除法運算法則最為重要的是化歸和歸納，即在本次教學中，應該選擇推理思想作為落實數學基本思想的首要任務.

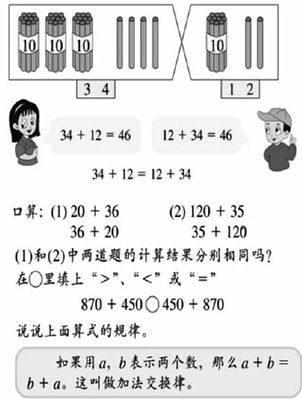
又如，浙教版三年級上冊第12頁“加法、乘法交換律”（如圖2），教材安排的內容非常全面和精致，首先利用“數形結合”的方法進行發現和猜想，然后進行舉例驗證，接著通過觀察算式的特征歸納“交換律”，最后將“交換律”用符號表示. 從數學思想方法來說，這里有數形結合思想、符號化思想、歸納思想，甚至也可以有演繹思想等. 事實上，短短的一節課不可能將這些思想方法一一落實，我們必須取舍，有所為有所不為. 顯然，這節課的首要任務是讓學生經歷不完全歸納的過程，凸顯推理思想.

2. “滲透”——落實的主要方式

數學是一門嚴謹的科學，但由于思想是思維活動獲得的結果，屬于隱性知識或緘默知識，一定是“所知必能言多”，所以本身不可能處理得條塊清晰、表述得完整無暇，“滲透”才是小學階段數學思想的主要方式. 如，一年級上冊“20以內退位減法”，學生通過探究逐步找出了四種方法：

教師在進行算法多樣化的算理交流和優化的同時，就已經滲透了數學推理等思想，不必教師總結或告訴孩子“推理”等的詞句. 當然，如果能在恰當的時機表達“每一種策略都有各自的道理”、“學數學一定要講道理”等潛移默化式語句，那就更加完美了.

除此之外，有時教學活動的本身就是很好的“滲透”，在一年級上冊“加法的認識”教學時，教師如能先呈現大量生活中的例子（如圖3），然后再引導到觀察方塊（見圖4）與圖3例子的相同點，最后得出4+3=7的加法算式. 盡管整個教學過程中不一定出現抽象、歸納等術語，但整個教學流程就是一個滲透了由生活的事到幾何圖的抽象思想，多種情況進行總結歸納的合情推理思想，這樣的學習累積終究會讓學生感悟、體會并學會應用.

更一般地說，“滲透”是小學生獲得數學思想的主要方式，在小學階段要對數學基本思想不要分出五花八門具體的數學思想方法和嚴密的定義，這種泛化處理只會折騰學生，并離思想越來越遠. 教學實踐中必須以數學知識技能的學習為載體，精心設計學習活動，營造出積極寬松的環境，讓學生在充分地觀察、比較、分析、猜想、思考的探究過程中領會方法，滲透數學思想.

3. “持續”——落實的重要保證

兒童的思維能力的發展由量變到質變、由低級到高級，經歷了一個比較復雜的過程，數學思想的滲透也需要遵循這個原則，即循序漸進、連續累積. 如果沒有前期計算教學中反復化歸、歸納的體會和運用，在學習分數除以整數，學生就很有可能出現不解和困難. 同樣，如果沒有在前面進行感受，多次體會化歸的數學思想，學生就不可能領會并探究在分數除以分數中進行這么復雜的算理推理.

典型的還有，在整數乘法教學中，“整十數乘一位數”是利用乘法口訣進行推算，如30 × 8 = 3 × 8 × 10 = 240；“兩位數乘一位數”也是利用前者的方法進行推算，如35 × 8 = 30 × 8 + 5 × 8；而“三位數乘一位數”的計算方法則更加開放和多元，如356 × 8 = 300 × 8 + 50 × 8 + 6 × 8，或356 × 8 = 350 × 8 + 6 × 8，或356 × 8 = 300 × 8 + 56 × 8，…正因為在每一次教學中都滲透轉化成原有知識進行解答的推理活動，學生有了深刻的感受和體會，慢慢發展為一種思維習慣和能力，后續的學習和探究也變得越來越精彩.

所以，教學中應該從整體著眼，把數學基本思想真正看成教學的有機組成，有目的有計劃地連續地進行數學思想滲透活動. 除了第一點提到的與課時目標一致時要重點滲透之外，與單元目標、知識系列目標一致時也要有意地、持續地去滲透，哪怕是“蜻蜓點水”，因為日積月累的“滴水”終能“穿石”.

【參考文獻】

[1]中華人民共和國教育部. 義務教育數學課程標準2011版[M].北京：北京師范大學出版社，2012.

[2]鄭毓信. 數學思維與小學數學[M]. 南京：江蘇教育出版社，2008.

[3]顧沛.小學數學教學也要注重滲透數學思想[J]. 小學教學：數學版，2012（8）.

[4]梁秋蓮. 讓學生在數學學習中獲得數學的基本思想 [J].小學數學教育，2012（3）.

[5]孫曉天. 關于數學基本思想的若干認識與思考[J].江蘇教育，2012（12）.