數形結合方法在高中數學教學中的應用

張秀蓮

摘 要： 數形結合的實質是把直觀圖像和數學中的抽象語言結合在一起，使形象思維與抽象思維有機結合，并將抽象轉化為直觀，化難為易。數形結合是高中數學教學的本質特點之一，將數形結合運用在高中數學教學中，可以使學生的理解能力、分析能力、觀察能力、綜合能力得到提高，為學生的數學學習提供有利條件。本文主要對數形結合法在高中數學教學中的應用進行分析。

關鍵詞： 數形結合 高中數學教學 應用

1.引言

將數形結合法運用在高中數學教學中，可以使學生繞過數學學習中的障礙，脫離各種繁瑣的理論推導，根據圖形數學函數進行理解并進行使用。數形結合可以將幾何與代數問題結合起來，讓代數問題得到較好的詮釋，使數學中復雜的問題得以明了化、簡單化。

2.將數形結合運用在高中數學教學中的作用

將數形結合運用于高中數學教學中的具體作用有：第一，數形結合的運用可以幫助學生發展形象思維，提高學生對數學的學習興趣，增強學生學好的信心。因為數學具有獨特的抽象性、形式化、符號化等特點，讓學生對數學產生一種冰硬、生冷的感覺，所以導致學生對學習數學的興趣較低，產生厭惡、枯燥的情緒[1]。將數形結合運用在高中數學教學中，可以降低學生學習的難度。在數學教學中，可以利用數形結合為代數提供相應的幾何模型，從而將問題本質直觀、形象地揭示出來。該方法減輕了學生的學習負擔，激發出學生對數學的學習興趣。第二，數形結合有利于學生對現代思維、意識進行樹立。數形結合的有效運用可以幫助學生對問題進行多角度、多層次的分析，讓學生形成放射性思維。且數形結合在一定的程度上可以引導學生將靜態思維與動態思維結合起來，通過聯系、變化、運動的觀點對問題進行思考，進而對事情的本質進行把握。另外，數形結合可以使形象思維和抽象思維相結合，從而給學生辯證思維的形成創造有利條件。

3.高中數學教學中數形結合的具體運用

3.1抽象函數中數形結合的有效運用

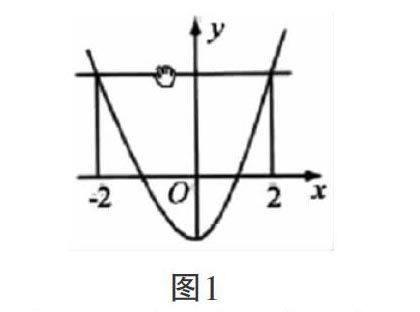
將數形結合運用在高中數學教學中，可以使學生在理解函數知識時更容易。在高中函數教學中，往往會碰到許多和函數性質有關的命題，學生在理解過程中會覺得比較困難，但是如果將數形結合運用在其中，學生就可以根據數形結合的特點解決問題。如在講解偶函數時，假設y=f（x）這個函數是偶函數，且其在區間（-∞，0）上為減函數，f（2）≤f（a），讓學生判斷出a的實際取值范圍。在面對此類抽象的問題時，如果直接運用數學推導對其進行解決就會顯得非常困難，但是根據圖形解決這種抽象的問題就會比較容易[2]。在解決該問題的過程中，首先應畫出相應的圖形，如圖1。

圖1

因此，通過圖1就可以看出該函數是偶函數，而且根據題目中的條件可以得出a的取值范圍。面對此類抽象的函數問題時，若能夠直接將函數圖形畫出來，只需根據偶函數的對稱定律就能夠直接得出正確答案。

3.2將數形結合運用在函數性質的記憶中

高中數學中的許多知識都比較繁瑣、抽象，學生可以根據數形結合解決這些抽象的問題，幫助學生對函數知識進行記憶、鞏固。如高中數學中三角函數的運用，在處理此類問題時，學生必須牢記tanx、cosx、sinx相關的函數性質，在記憶過程中學生可以運用數形結合的方法，這樣不但可以節省時間，而且輕輕松松就可以將其全部記住。學生對sinx函數的相關性質進行記憶時，若將sinx的具體圖形畫出來，學生就可以很容易地區分清楚sinx的單調區間、周期、奇偶性、對稱性；就是說學生只要將sinx的圖形記住，就可以完全將sinx的性質記住。

3.3解決函數問題中數形結合的具體運用

從任何一個階段的教學教學宗旨來看，其都是為了對學生解決實際問題的方法進行鍛煉，高中數學教學中將此類問題稱作應用題。在解決應用題的過程中，并不是根據相關數字就可以使問題得到解決，也不是單靠一幅圖就可以解釋清楚的。需要學生利用具體圖形將問題核心展現出來，再利用數學推導才可以得出正確答案[3]。如在許多求值域、最值的函數題目中，上述問題就會體現出來，但是學生利用數形結合對其進行處理就可以很快得出正確答案，這樣還可以使學生探索的精神得到激發，從而更積極主動地學習數學知識。

4.結語

將數形結合運用在高中數學教學中可以使學生解題思維得到不斷發展，增強解題能力，對學生數學思維的發展也有重要影響。數形結合可以利用幾何問題映射代數問題，使代數問題與幾何問題相互轉換，使學生將抽象思維和形象思維結合起來，降低學生解題的難度。

參考文獻：

[1]成彥盛.高中數學教學中數形結合方法的有效應用[J].教育界，2014，46（20）：357-358.

[2]農忠勇.“數形結合”思想在高中數學教學中的重要作用[J].讀寫算（教育教學研究），2013，38（30）：457-458.

[3]洪榕波.“數形結合”思想在高中數學中的應用[J].華章，2013，35（12）：468-469.