論如何在教學中體現高等數學的應用性與現實性

歐陽正勇

（佛山科學技術學院 計算科學與數學系，廣東 佛山528000）

論如何在教學中體現高等數學的應用性與現實性

歐陽正勇

（佛山科學技術學院 計算科學與數學系，廣東 佛山528000）

摘要：針對許多高校學生發出的高等數學無用論調，筆者從教材的結構模式、學科專業特點和教學方式等幾個方面對高等數學教學內容、教學方式和方法進行創新，用以說明數學應該在各學科教學中展現現實性和應用性.由點及面，對普通高校的高等數學課程的改革提供參考.

關鍵詞：高等數學；教學改革；應用性；現實性

數學作為一門基礎學科，往往被人認為是脫離實際的空中樓閣，大部分人沒有認識到數學的實用性，認為數學是數學家無聊發明出來的東西，而不知數學本身來源于實際生活，也能更好的服務于科學生產.在人類歷史的發展中，原始算術的出現、歐幾里德幾何的形成、十七世紀微積分的誕生和現代計算機科學的實現，數學無不顯示著對現實社會的促進作用.以航海交通領域為例，大到全球的GPS衛星定位,小到一個個港口物流公司的管理運作，數學無所不在.但是數學在當今時代各個領域內的實在作用，尤其在高校中,卻經常受到質疑.在高科技技術發展的光環背后，《高等數學》成了一門可有可無的課程.

要改變這種狀況,筆者作為高校的數學教師從以下幾個方面,說明數學在各學科教學中展現的現實性.由點及面，對于普通高校的高等數學課程的改革給予參考.

1　改變傳統教材的結構模式

原有傳統高等數學課程的學科體系讓學生失去思考的主動性.傳統教材由定義--定理--定理證明--理論應用，讓學生認為數學理論與應用是理所當然產生的，是數學家閑來無聊論證的，所謂應用也是由理論出發去尋找合適的應用的.而事實上，絕大部分的數學問題來源于現實，由于具備現實普遍性，人們才利用數學符號與公式抽象化解決問題.而且數學理論建立也都是建立在數學家們艱苦卓絕的努力上的.也就是說，在學習高等數學時，如果從實際問題出發，或從科學家解決問題的思路出發，對于培養學生思考問題、解決問題的能力是有很大提高的.從實際問題出發，到實際問題的解決，再到新問題的產生，這樣不斷循環提高，讓學生在高等數學課堂上不再被動的接受枯燥的理論，而是著眼于具體問題的解決方法和實際應用，學習解決問題的方法［1］.

這需要教師對教學內容進行合理調整，對教材的依賴性較小，對教師的知識背景與能力要求較高.按傳統的高等數學課程章節的知識點分類，提供大量的數學模型，將知識點穿插在模型中，讓學生在解決實際問題中掌握知識點.

引入matlab、mathmatica等數學軟件技術，將大大提高數學的實用性與可操作性.

2　將數學與專業學習相結合

將數學模型引入課堂是比較可行的辦法.將知識點按應用分類，根據學生自身專業建立數學模型，比如物流、國際貿易專業應多準備相關經濟類的問題建立數學模型，工程機械類專業準備工程類的數學模型.整個高等數學課程由幾個循序漸進的數學模型來構建，并與專業知識掛鉤，對學生的職業技術能力與知識素養有極大的提高.如何將理解數學概念落實到用數學思想和數學概念消化并吸收應用到工程概念與原理上.例如“案例驅動”是最好的將理論與實踐結合的方法［2］.

2.1案例1

我們把易拉罐看作是一個圓柱體，是否發現百事可樂、可口可樂、健力寶等等飲料公司出售的易拉罐的半徑與高之比是多少？請測量一下，并思考為什么這些公司會選取這樣的比例尺寸？

工業設計在考慮外包裝美觀與運輸便利的同時，務必考慮在容積一定的情況下所用材料最少、焊接加工等制作費用最低的成本問題，這類問題就是數學上最常見的優化問題：最值問題.

2.2案例2

2006年以來，面對中國國內房價暴漲，經濟學家預測：2012年中國房價將會出現拐點.試解釋這句話的意思.拐點是曲線凹凸的分界點，描述曲線增減速度的變化.經濟學家預測房價出現拐點對應前期房價的高速增長，意味著房價的增長速度將會放緩.

這些案例和練習都可以具有針對性的面向不同專業的學生，引起學生對本專業的學習興趣，加深對數學基礎知識的理解，使基礎課程與專業應用相呼應.

3　體現教學方法的多樣性

希臘歷史學家Plutarch說“思想不是一個需要填充的容器，而是需要點燃的木頭”，教師需要花更多的時間點燃學生們的創造力、想象力和解決問題的能力.不能將高等數學僅僅看作是理論基礎課，對于大部分應用型本科院校高等數學更多的側重于應用數學方面，而不是理論研究.作為應用數學必然與多學科交叉應用，并利用計算機輔助教學，重視Matlab、Mathmatica等數學軟件的學習，學習數學思想重于學習數學知識，學習數學方法重于學習數學理論，學習數學工具重于理論推導，將數學知識跟計算機能力有機結合.壓縮理論課時，增加上機課時.布置論文或報告形式的作業.考試考查方面應更多的側重應用能力，通過積極地與學生交流，不斷調整教學方式.比如讓學生建模后上機計算,利用計算機輔助手段解決數學問題與應用問題是當今世界高校潮流趨勢.

3.1案例(線性規劃模型的實例)

家具公司生產桌子和椅子，用于生產的勞力共計450個工時，木材共有4立方米,每張桌子要使用15個工時，0.2立方木材，售價80元.每張椅子使用10個工時，0.05立方木材，售價45元.問為達到最大的收益，應如何安排生產？

案例分析：

（1）案例求什么？

①生產多少桌子？x1張桌子

②生產多少椅子？x2張椅子

（2）案例優化什么？

收益最大值Maxf=80x1+45x2

（3）實際的限制條件是什么？

原料總量0.2x1+0.05x2≤4

勞力總數15x1+10x2≤450

3.2建立模型

以產值為目標取得最大收益.設：生產桌子x1張、椅子x2張(決策變量)，將目標優化為：Maxf=80x1+ 45x2.

對決策變量的約束：

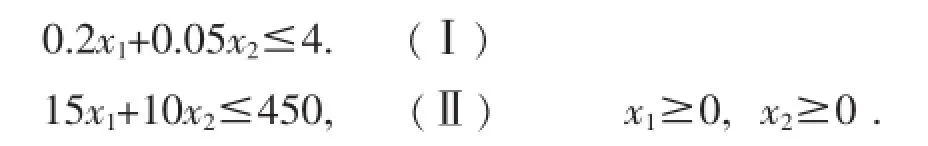
3.3模型求解

3.3.1方法（1）圖解法（用于決策變量是2維）

圖1　線性規劃模型實例

線性規劃問題的目標函數(關于不同的目標值是一族平行直線)目標值的大小描述了直線離原點的遠近,并且最優解一定在可行解集的某個極點上達到［3］(穿過可行域的目標直線組中最遠離或接近原點的直線所穿過的凸多邊形的頂點).

3.3.2方法（2）用EXCEL—Solver實現

模型中的數據直接輸入EXCEL工作表中（見圖2）.其中決策變量初始的值可以任意給出，它們是可變的，軟件最后將給出最優解的值.SUMPRODUCT是EXCEL的一個內置函數，表示兩個向量或矩陣對應元素乘積的和.

圖2　數據輸入

接下來選擇工具菜單中的規劃求解，即可得到最優解為2 200.

3.3.3方法（3）用Matlab實現--lp線性優化函數

線性優化問題即目標函數和約束條件均為線性函數的問題.其標準形式為：

其中A∈Rm×n,m≤n（通常m＜n），b∈Rn,c∈Rn均為數值矩陣.

將Maxf=80x1+45x2,

轉化為Minf=-80x1-45x2,

Sub.to0.2x1+0.05x2≤4.

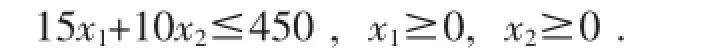
程序如下：

c=［-80,-45］;a=［0.2,0.05;15,10］;b=［4,450］;vlb=［0,20］;vub=［0,45］;

［x,lam］=lp(c,a,b,vlb,vub)（參數vlb,vub給出變量的上下邊界的約束）.

說明：x的解為最優解，lam說明約束條件發揮了作用.

3.3.4方法（3）用LINDO實現

我們可以直接在下面的窗口輸入LP模型［5］.見圖3.

圖3　輸入簡單的優化模型

輸入后，用鼠標單擊LINDO軟件工具欄中的圖標，或從菜單中選擇Solve│Solve(Ctrsl+S)命令，則LINDO開始編譯這個模型，編譯沒錯誤馬上開始求解，求解時會顯示LINDO求解器運行狀態窗口，里面的“Objective”對應的數字2 200就是最優解.

這個例子中的LP模型太小了，我們可能還沒來得及看清結果輸出的界面，最優解就出來了，并馬上彈出詢問你是否需要作靈敏性分析的對話框，可以先選擇“否N”按鈕，這個窗口就會關閉.如果你在屏幕上沒有看到求解的結果，那么可以用鼠標選擇LINDO的主菜單 “Window”,會發現有一個子菜單項“Reports Window”，這就是最終結果的報告窗口.用鼠標選擇“Window│Reports Window”，就可以查看到窗口的內容（見圖4）.

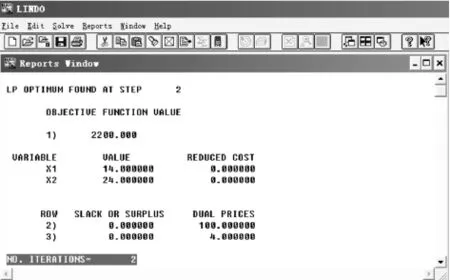
圖4　最優解及各變量的取值

“LP OPTIMUM FOUND AT STEP 2”表示單純形法在兩次迭代后得到最優解.“OBJECTIVE FUNCTION VALUE 1)2 200.000”表示最優目標值為2 200.000（在LINDO中目標函數所在的行總是被認為是第1行，這就是這里“1）”的含義）.

“VALUE”給出最優解中各變量的值：x1=14.000 000，x2=24.000 000.“SLACK OR SURPLUS（松弛或剩余）”給出約束對應的松弛變量的值：第2、3行松弛變量均為0，說明對于最優解來講，兩個約束均取等號，即都是緊約束.“DUAL PRICES”給出對偶價格的值.“NO.ITERATIONS=2”表示用單純形法進行了兩次迭代（旋轉）.

上面這個案例充分的體現了數學課程的多變、靈活、實用的特性.

高等數學課程應著眼于提高學生的以下幾方面能力：（1）對數學的整體性和知識點在現代數學中的位置及在經濟發展中的直接和間接用途有所了解、有所認識.（2）從實際問題中抽象出各類數學問題的能力. （3）能從多角度觀察問題，能用多種方法解決問題.

在我國大力發展教育事業的大背景下，數學作為一門基礎課程對各應用學科都起著極其重要的現實作用.然而“以學生為中心”的課程教學模式沒有理想中那么簡單，是要學生在已有的知識結構上通過吸收外來信息最終建構個人體系.特別是對于在傳統教學模式中成長起來的教師們來說，轉變教學模式是一個長期的緩慢的甚至可能會出現反復的過程.

課程教學模式改革的趨勢之一是向應用型本科教育方向發展，高等數學課程的教學改革也必將迎來新一輪的挑戰.筆者在借鑒國內外先進的教學理念的基礎之上，結合我國高校教育的特點，通過對高等數學課程的教學模式改革與研究，以求建立一種創新、有效的教學模式.這種教學模式，應當體現創新教育教學的特色，追求教學的實際效益，既要適應學生的實際，又要適應社會實際的需求，要有明確的崗位能力目標；要教會學生完整地做好一件事情，讓學生由“學會”變為“會學”；強調學生的能力培養，評價標準著重衡量學生的能力水平.筆者旨在通過對教學模式的研究與實踐，促進高等數學教育教學質量提高，也為本科院校開展教育改革研究提供一些有益借鑒與參考.

參考文獻：

［1］張霞,張庚家.用問題激發學生學習高等數學興趣的研究［J］.大學數學,2006,22(2):23-25.

［2］楊曙光.高等數學應用問題教學探索［J］.高等數學研究,2014,17（4）：119-122.

［3］姜啟源，謝金星，葉俊.數學模型［M］.第三版.北京：高等教育出版社,2005.

［4］王沫然.MATLAB 5.X與科學計算［M］.北京：清華大學出版社,2000.

［5］謝金星，薛毅.優化建模與LINDO/LINGO軟件［M］.北京：清華大學出版社,2005.

［6］王愛華.新形勢下改進高等數學教學實踐與探索［J］.教育與職業,2013(24）：119-121.

（責任編輯：李婉）

中圖分類號：O13

文獻標識碼：A

文章編號：1007-5348（2015）02-0073-06

［收稿日期］2014-09-21

［基金項目］廣東省教改項目（GDJG20141204）.

［作者簡介］歐陽正勇（1978-），男，湖北漢川人，佛山科學技術學院計算科學與數學系講師，博士；研究方向：主要從事微分方程.

How to Show Application and Reality of Higher Mathematics in Teaching

OUYANG Zheng-yong
（Department of Mathematics,Foshan University,Foshan,528000，Guangdong,China）

Abstract:For useless argument of higher mathematics from many students in university,this paper proposes innovation of higher mathematics teaching content and teaching ways from several aspects such as structure model,characteristics of subjects and teaching methods and so on,which can be used to explain that the mathematics should show the reality and application in the teaching.And from the point to surface,it could provide reference for reform of higher mathematics curriculum in colleges and universities.

Key words:higher mathematics;teaching reform;application;reality