“三重聯系”的數學課堂教學設計之意涵、作用與要求

【摘 要】為提高數學課堂教學的實效，應在理解與把握“基于‘三重聯系的數學課堂教學設計”意涵的基礎上，充分發揮其有利于提高學生數學學習的興趣、有利于提升學生數學有意義記憶的水平、有利于發展學生數學聯想的能力等作用，并努力做到它所要求的整體系統、動態生成與以學生為本的目標。

【關鍵詞】三重聯系;教學設計;意涵;作用;要求

【中圖分類號】G633.6 【文獻標識碼】A 【文章編號】1005-6009（2015）26-0021-02

【作者簡介】徐文彬，南京師范大學課程與教學研究所（南京，210097）教授、博士生導師。

數學的最大特征是其高度的抽象性、嚴密的邏輯性和廣泛的應用性。而大多數接受過基礎教育（甚至高等教育）的成人對數學的印象與此不無一致：好枯燥、好乏味、（好似）無處不用數學。為解決此類“一致性矛盾”，《義務教育數學課程標準（2011年版）》已為我們指明了努力方向：數學課堂教學應讓學生“體會數學知識之間、數學與其他學科之間、數學與生活之間的聯系……”那么，我們應如何基于“三重聯系”來設計課堂教學呢？

一、基于“三重聯系”的數學課堂教學設計之意涵

“基于‘三重聯系的數學課堂教學設計”主要有以下幾項意涵：首先，應在充分理解所教授的數學學科內容領域（譬如，數與代數）內部各部分知識之間的內在關聯性的基礎上，分析該內容領域與其他內容領域（譬如，圖形與幾何、統計與概率、綜合與實踐）之間的“外部”關聯性;其次，應在充分了解當下兒童的實際生活和社會發展狀況的前提下，探討所教授的數學學科內容領域與其所存在的各種現實的或潛在的關系;第三，應在充分知曉所教學生所學其他學科內容的基礎上，研究所教授的數學學科內容領域與其他學科之間的關系;最后，應結合所教學生的年齡特征與實際情況，有針對性地設計相應學科內容領域的學習目標或教學目標、學習活動或教學活動、學習評價或教學評價，并始終關注它們之間的相互協調與一致性問題。

二、基于“三重聯系”的數學課堂教學設計之價值

興趣是最好的老師，而唯有聯系學生當下“深陷、遭遇的”生活實際與社會實踐，才有可能引發學生的注意，以至培養學習的興趣、思考的習慣。數學歷來被認為是中學最為“枯燥、乏味的”一門課程，不少學生深受“努力學、學不好、好難學、學不會……”的境地，以致患有“數學恐懼癥”。而解除這些學生的痛苦，并提高其他學生學習數學的興趣的良方之一便是，把數學與他們的實際生活與社會實踐聯系起來，思考并設計課堂教學。

機械記憶是最不牢靠的，而有意義的記憶則是可以長久儲存的。數學常常給人以“幾何難、代數繁、三角公式背不完”的刻板印象。這其中的緣由之一可能就是我們的數學教學，既缺乏數學各領域內部的聯系，又少有各領域之間的內在關聯。因此，破除這一“刻板印象”的方法之一就是，就中學數學的所有內容來思考其各領域內部以及各領域之間的本質聯系，并設計其課時新授、單元復習、階段復習（包括期中、期末）以及相應的練習或習題課與試卷講評的教學設計。

任何事物都是質與量的統一體，任何“沒有質的量”與“沒有量的質”都是不可想象的。而數學是只研究事物的量，不涉及事物的質。所以，數學學科是關于“純粹思想事物”的知識體系，抽象性極高、邏輯性極強。但是，數學的發生、發展和應用，一刻也沒有離開過其他學科的滋養。曾經，物理的“養育之功”最大;現在，幾乎沒有哪一門學科不能給予數學以“營養”。因此，僅就“歷史重演律”而言，也需要我們把數學與其他學科聯系起來思考并設計課堂教學，培養與發展學生的數學聯想能力。

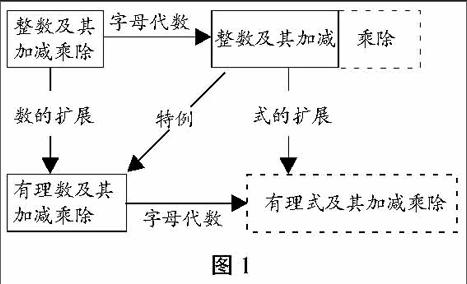
譬如，當學生對相對獨立的數學知識單元的數學事實積累到一定的程度時，就應鼓勵、引導、幫助學生自主地通過組織化的手段獲得逐步系統化的知識，形成或優化相應的認知結構（知識結構的內化）。例如，在學完《整式》這一單元之后，就應創設情境促使學生主動地對下列知識結構（見圖1）進行內化。這里既要強調整數與整式、有理數與有理式的共同點，也要注意其區別。

圖1

（注：要在虛線框內的內容還沒有學習前進行組織化。）

由圖1我們約略可知“整數→有理數”——“整式→有理式”的結構，這里不僅有提升學生數學有意義記憶水平的考慮，更有培養與發展學生數學聯想能力的設計，甚至還有培養學生數學學習興趣的深意。

三、基于“三重聯系”的數學課堂教學設計之要求

首先，“基于‘三重聯系的數學課堂教學設計”要求我們的教學設計應是整體系統的。其一，應把數學課堂教學置于學校教育當中來考慮;其二，應把初中數學課堂教學置于義務教育階段乃至基礎教育階段（包括幼兒園與高中）數學教育當中來考慮;其三，應整體地考慮初中數學教育中四大內容領域的課堂教學;其四，應系統地考慮各內容領域的課堂教學設計;其五，應系統地考慮每一個內容領域中各年級各學期的數學內容的課堂教學設計;其六，應置“課時教學備課”于單元教學設計當中來考慮。譬如，初中生常常會在學習“運用一元一次方程解決實際問題”時仍然習慣于運用“算術方法”來求解，何以會如此呢？小學“歸類解文字應用題”之故也。如果我們不能“回到小學”，我們甚至連這類問題也無法解釋，何談解決？

其次，“基于‘三重聯系的數學課堂教學設計”要求我們的教學設計應是動態生成的。盡管任何形式的課堂教學設計都有預設與生成，但是，“基于‘三重聯系的數學課堂教學設計”更關注動態生成。其一，“三重聯系”甚至就其中的“數學知識之間的聯系”也不僅僅是確定不變的邏輯關系，更不是“史實”似的鐵律關系，而是社會理解的，深蘊人文性;其二，就當下兒童數學學習的背景資源而言，我們教師可能無論如何也無法窮盡其所有，這便給我們帶來了極大的挑戰，教師既需要對此保持敏感，又需要果斷決策。

再次，“基于‘三重聯系的數學課堂教學設計”要求我們的教學設計應是以學生為本的?！耙詫W生為本”不能僅僅局限于學生的學習結果（尤其是學習成效）或學習過程（尤其是學習活動），而應更多地關注他們對自己的學習過程與學習結果的主觀感受，并據此來處理或協調課堂教學中的各種對稱關系：課前預設與課堂生成，教師主導與學生自主，教學進程與學習進程，課本知識與學生經驗，學科思維與學生思維，學生的個體差異和個別差異及其給予教師的啟發，學生的學習結果和學習過程及其給予學生的主觀感受，等等。

上述所謂“基于‘三重聯系的數學課堂教學設計之要求”是相對于我們慣常的課堂教學設計而言的。如果“慣常的”已變成“怪異的”，而“基于‘三重聯系的數學課堂教學設計”已變成慣常的，那么，上述所謂的要求都將不成為問題，這也正是我們所期待的。

【參考文獻】

[1]義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2011.

[2]徐文彬.關于數學文化視域中數學教學的若干思考[J].課程·教材·教法，2012（11）.

[3]徐文彬.如何認識《義務教育數學課程標準》中的三重聯系[J].江蘇教育：小學教學，2013（02）.

[4]徐文彬.基于“三重聯系”的課堂教學設計——以《一元一次方程》單元復習為例[J].江蘇教育：中學教學，2013（05）.

[5]徐文彬.關于數學文化視域中數學學習的構想[J].數學教育學報，2014（05）.

【基金項目】2011年度江蘇省教育科學規劃重大課題（A/2011/08）：基礎教育課程改革重大理論與實踐問題的深化研究