車輛工程專業學生工程素質的一種評估方法

趙振東

摘要：良好的工程素質是車輛工程專業人才培養的重要目標，科學的素質評估對反映教學的真實情況、提高教學質量至關重要。針對現行定性評估方法的局限，本文介紹了層次分析法，提出了運用層次分析法對學生工程素質進行評估的方法。應用示例表明該方法是可行的。

關鍵詞：層次分析法；工程素質；評估

中圖分類號：G640 文獻標志碼：A 文章編號：1674-9324（2015）48-0171-03

深化教育改革與發展，培養高素質的創新型和工程應用型人才是高等院校，尤其是應用型工科大學教學的基本任務[1]。其中，教育評估方法和體系的建立則是學生工程素質培養的前提和基礎[2]。

我校車輛工程專業的學生畢業后主要從事汽車設計、開發及性能匹配等方面的工程實踐活動，因此，良好的工程素質是車輛工程專業人才培養的重要目標。學生工程素質評估屬于系統工程范疇，涉及的因素及層次較多，在實際評估中會面臨很多問題。一般研究停留在定性評估方面，而定量方面尚未得到研究。層次分析法正是一種定量與定性分析相結合的系統分析方法，可以用來解決學生工程素質的評估問題。

層次分析法是一種對定性問題進行定量分析的多準則決策方法。它的特點是模擬人的決策思維過程，把要解決的問題進行組合分層，然后針對每一層次中各因素的相對重要程度，根據人們對于客觀事物的認識進行定量描述，并計算出每一層次中全部因素相對重要性的權值。最后，綜合計算各層因素相對總目標重要性的權值，以得到所有層次之間的總排序結果，從而實現解決多因素復雜系統的決策評估問題[3，4]。

一、方法與步驟

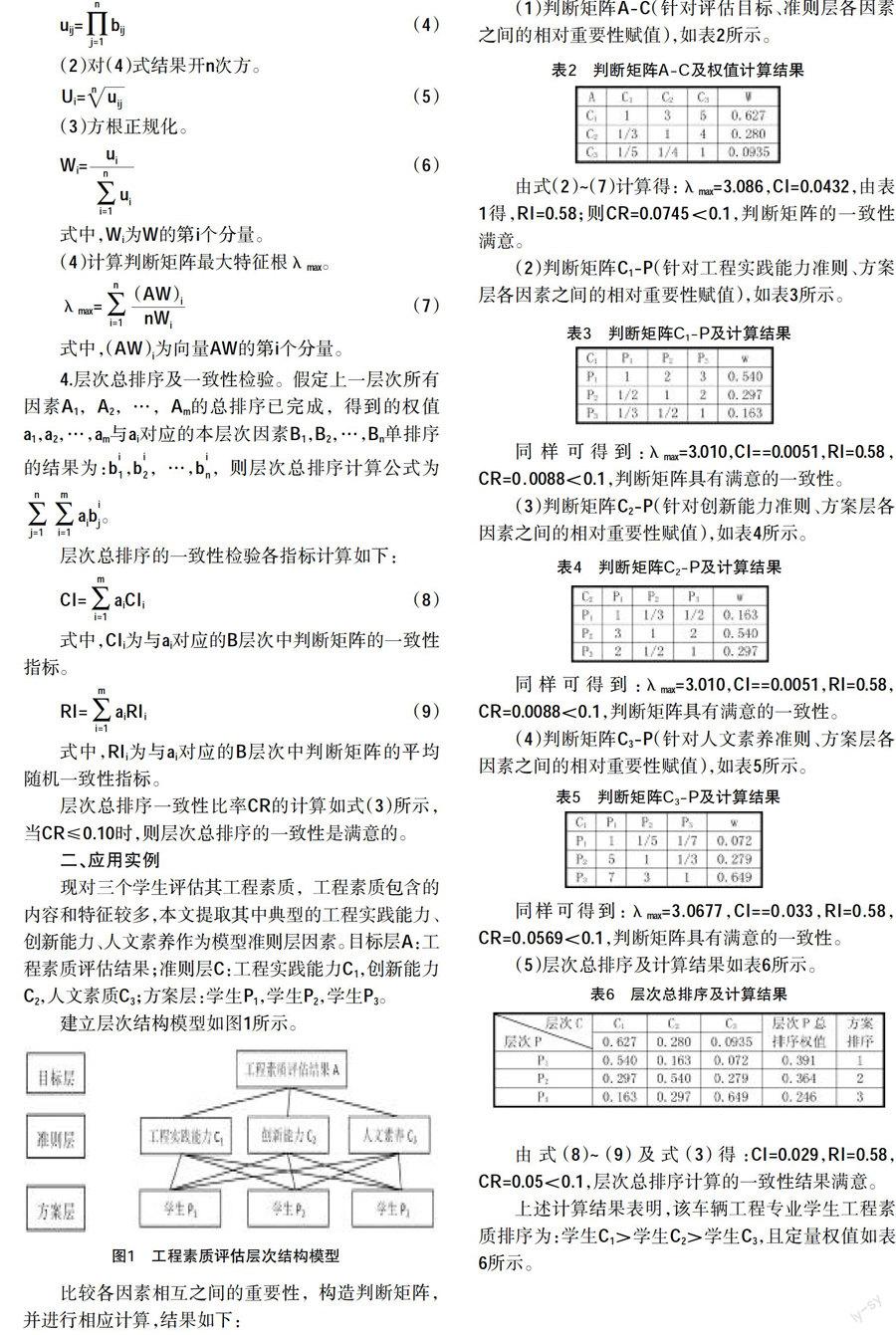
1.建立層次結構模型。將所包含的因素按照隸屬關系及相互影響進行分層，一般分為目標層（最高層）、準則層（中間層）和方案層（最低層），各層及各因素之間通過連線來表達相互關系，層次結構模型如圖1。

2.構造判斷矩陣[3]。判斷矩陣是層次分析法的核心。假定判斷矩陣某元素bij，那么針對上一層次某因素，需要給出Bi與Bj的相對重要性。重要性賦值一般采用1～9及其倒數的比例標度，如bij=1，表示Bi與Bj一樣重要，如bij=9，表示Bi比Bj極端重要。

3.計算單一準則下各元素的相對權重及一致性檢驗[3]。對上一步所得到的判斷矩陣B，計算其特征根和特征向量，如下式所示。

層次總排序一致性比率CR的計算如式（3）所示，當CR≤0.10時，則層次總排序的一致性是滿意的。

二、應用實例

現對三個學生評估其工程素質，工程素質包含的內容和特征較多，本文提取其中典型的工程實踐能力、創新能力、人文素養作為模型準則層因素。目標層A：工程素質評估結果；準則層C：工程實踐能力C1，創新能力C2，人文素質C3；方案層：學生P1，學生P2，學生P3。

建立層次結構模型如圖1所示。

比較各因素相互之間的重要性，構造判斷矩陣，并進行相應計算，結果如下：

（1）判斷矩陣A-C（針對評估目標、準則層各因素之間的相對重要性賦值），如表2所示。

由式（2）～（7）計算得：λmax=3.086，CI=0.0432，由表1得，RI=0.58；則CR=0.0745<0.1，判斷矩陣的一致性滿意。

（2）判斷矩陣C1-P（針對工程實踐能力準則、方案層各因素之間的相對重要性賦值），如表3所示。

同樣可得到：λmax=3.010，CI==0.0051，RI=0.58，CR=0.0088<0.1，判斷矩陣具有滿意的一致性。

（3）判斷矩陣C2-P（針對創新能力準則、方案層各因素之間的相對重要性賦值），如表4所示。

同樣可得到：λmax=3.010，CI==0.0051，RI=0.58，CR=0.0088<0.1，判斷矩陣具有滿意的一致性。

（4）判斷矩陣C3-P（針對人文素養準則、方案層各因素之間的相對重要性賦值），如表5所示。

同樣可得到：λmax=3.0677，CI==0.033，RI=0.58，CR=0.0569<0.1，判斷矩陣具有滿意的一致性。

（5）層次總排序及計算結果如表6所示。

由式（8）～（9）及式（3）得：CI=0.029，RI=0.58，CR=0.05<0.1，層次總排序計算的一致性結果滿意。

上述計算結果表明，該車輛工程專業學生工程素質排序為：學生C1>學生C2>學生C3，且定量權值如表6所示。

三、結語

本文通過層次分析法建立了學生工程素質評估數學模型，通過計算，得到方案層各因素（各學生）相對于工程素質評估結果（總目標）的相對重要性次序的組合權值，從而得到學生工程素質評估結果。計算示例表明，本方法可行。

當然，學生素質的綜合評估是一項較復雜的系統工程，同時，各個學校的車輛工程專業培養目標的側重點有所不同，因此，很難制訂固定的各項指標的評價標準，在實際使用中，需要根據具體情況對評價標準做適當修改。

參考文獻：

[1]鄭燕萍，閔永軍，蔡偉義，等.汽車設計專業實踐教學改革的探討與實踐[J].蕪湖職業技術學院學報，2009，（1）：76-78.

[2]何兆華.迎接知識經濟挑戰，構建發展性學生素質評估體系[J].陜西教育學院學報，2001，17（2）：5-9.

[3]譚躍進.定量分析方法[M].第2版.北京：中國人民大學出版社，2006.

[4]韓軍民，劉洪甫，李雪，等.模糊層次分析法在矩陣論教材評價方面的應用[J].教學的實踐與認識，2012，42（16）：7-12.