排列組合的簡單應用

魏偉

【摘要】排列組合是一種基本的計數方法，在近代科學研究中有重要地位，從中小學現行的課程來看，是學生學習概率統計知識的基礎，而且在安排調配等日常生活和工作中有大量應用。

【關鍵詞】組合問題 ?組合模型 ?排列問題 ?排列模型 ?元素

【中圖分類號】G623.5 ? ? ? ? ? ? ? ? ? ? ? ? ?【文獻標識碼】A ? ? ?【文章編號】2095-3089（2015）11-0136-02

一、排列組合的基本理論和公式

排列與元素的順序有關，組合與順序無關.如231與213是兩個排列，而2+3+1的和與2+1+3的和是一個組合。?1.兩個基本原理是排列和組合的基礎

加法原理：做一件事，完成它可以有n類辦法，在第一類辦法中有m1種不同的方法，在第二類辦法中有m2種不同的方法，……，在第n類辦法中有mn種不同的方法，那么完成這件事共有N=m1+m2+m3+…+mn種不同方法。

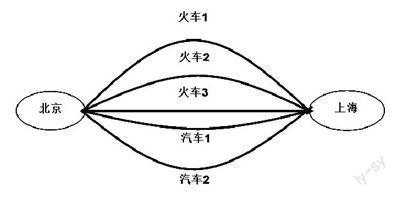
問題：從北京到上海，可以乘火車，也可以乘汽車。一天中火車有3班，汽車有2班.那么一天中，乘坐這些交通工具從北京到上海共有多少種不同的走法？

對于這個問題，首先要弄清楚這道題是要完成從北京到上海這件事，只要從北京到上海，就算完成了這件事.其次，從北京到上海有幾類走法？

乘法原理：做一件事，完成它需要分成n個步驟，做第一步有m1種不同的方法，做第二步有m2種不同的方法，……，做第n步有mn種不同的方法，那么完成這件事共有N=m1×m2×m3×…×mn種不同的方法。

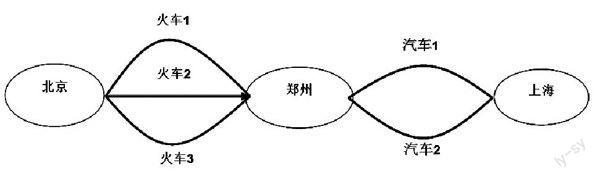
問題：從北京到上海，要從北京先乘火車到鄭州，再于第二天從鄭州乘汽車到上海，一天中從北京到鄭州的火車有3班，從鄭州到上海的汽車有2班，那么兩天中，從北京到上海共有多少種不同的走法？

無論單獨乘火車或汽車都不能從北京直接到達上海，要從北京到上海必須分兩步，第一步要先到鄭州，然后才能從鄭州到達上海，只有這兩步都完成了，才能從北京到達上海.從北京到鄭州乘火車有3種走法，再從鄭州到上海乘汽車有2種走法，并且兩步依次完成后，才能到達上海，所以共有3×2 = 6種不同的走法。

這里要注意區分兩個原理，要做一件事，完成它若是有n類辦法，是分類問題，第一類中的方法都是獨立的，因此用加法原理;做一件事，需要分n個步驟，步與步之間是連續的，只有將分成的若干個互相聯系的步驟，依次相繼完成，這件事才算完成，因此用乘法原理.這樣完成一件事的分“類”和“步”是有本質區別的，因此也將兩個原理區分開來。

2.排列

排列：從n個不同元素中，任取m（m≤n）個元素，按照一定的順序排成一列，叫做從n個不同元素中取出m個元素的一個排列。從排列的意義可知，如果兩個排列相同，不僅這兩個排列的元素必須完全相同，而且排列的順序必須完全相同，這就告訴了我們如何判斷兩個排列是否相同的方法。

3.組合

組合：從n個不同元素中，任取m（m≤n）個元素并成一組，叫做從 n個不同元素中取出m個元素的一個組合。

從組合的定義知，如果兩個組合中的元素完全相同，不管元素的順序如何，都是相同的組合;只有當兩個組合中的元素不完全相同時，才是不同的組合。

這里要注意排列和組合的區別和聯系，從n個不同元素中，任取m（m≤n）個元素，“按照一定的順序排成一列”與“不管怎樣的順序并成一組”這是有本質區別的。

二、用排列組合知識解決問題

最重要的是在計算式分析是分類還是分步，是排列還是組合問題，在分析中總結計算方法，進而歸納為排列組合問題，即利用排列組合公式計算。

1. 排列問題

例1：組數

用1、2兩個數可以組成多少個不同的兩位數？

可以組成12，21，2個兩位數。

2×1=2（個）。

用1、2、3三個數可以組成多少個不同的兩位數？

可以組成12，13，21，23，31，32，6個兩位數。

3×2=6（個）。

用1、2、3、4四個數可以組成多少個不同的兩位數？

猜想：4×3=12（個）？

可以組成12，13，14，21，23，24，31，32，34，41，42，43，12個兩位數。

4×3=12（個）。

用1、2、3、4、5五個數可以組成多少個不同的兩位數？

計算：5×4=20（個）。

用1、2、3、4、5......n個數可以組成多少個不同的兩位數？

n×（n-1）（個）。

猜想：用1、2、3、4、5......n個數可以組成多少個不同的三位數？

n×（n-1）×（n-2）（個）。

猜想：用1、2、3、4、5......n個數可以組成多少個不同的n位數？

n×（n-1）×（n-2）…3×2×1=n！（個）。

上述猜想可以用數學歸納法驗證驗證，此類組數問題為排列問題，我們用排列數計算公式來計算。

2. 綜合應用

例2：0，1，4，7和小數點可以組成多少個小于1的三位小數？

解析：整數部分只能是0，其余三個數字全排列P（3，3）=3×2×1=6（個）。

例3：由數字0、1、2、3、4按要求組數。

①可以組成多少個不同的五位數 ？

②小于20000的自然數。

①不同的五位數，分析最高位不能為0，所以最高位有4種選法，其余4個數字全排列（P4，4）=4×3×2×1=24，24×4=96（個）。

②小于20000的自然數 ，分析萬位可以選擇2，3，4，其余的四個數字全排列P（4，4）=4×3×2×1=24，24×3=72（個）。

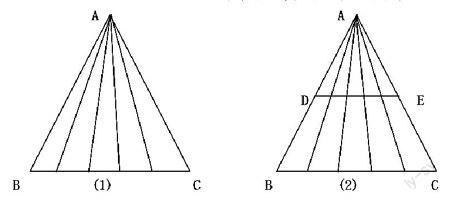
例4 ?圖中各有多少個三角形？

解析：圖（1）中任意兩條從A點引出線段都可以和線段BC上的一段組成一個三角形，是組合問題C（6，2）=6×5÷2=15（個）。

圖（2）中第三條邊可以是線段BC或線段DE的一部分，第三條邊有兩種選法，C（6，2）×C（2，1）=30（個）。

例5：用0、1、2、3、4、5、6、7、8、9這十個數字能夠組成______個沒有重復數字的三位數。

解析：用這十個數字排列成一個不重復數字的三位數時，百位上不能為0，故共有9種不同的取法.因為百位上已取走一個數字，所以十位上只剩下9個數字了，故十位上有9種取法。同理，百位上和個位上各取走一個數字，所以還剩下8個數字，供個位上取。

所以，組成沒有重復數字的三位數共有9×9×8=648（個）。

例6：一個口袋中有4個球，另一個口袋中有6個球，這些球顏色各不相同，從兩個口袋中各取1個球，共有多少種不同結果？

解析：從兩個袋子里各選一個C（4，1）×C（6，1）=4×6=24（種）。

例7：有9名乒乓球運動員參加比賽，每兩個運動員都要比賽一場，一共有多少場比賽？

解析：組合問題C（9，2）=9×8÷2=36（場）.

例8：甲、乙、丙、丁四個同學排成一排，從左到右數，如果甲不排在第一個位置上，乙不排在第二個位置上，丙不排在第三個位置上，丁不排在第四個位置上，那么不同的排法共有______種。

解析：因每個人都不排在原來的位置上，所以，當乙排在第一位時，其他幾人的排法共有3種;同理，當丙、丁排在第一位時，其他幾人的排法也各有3種。因此，一共有9種排法。

例9：用1克、3克、9克三個砝碼（砝碼只能放在一個秤盤中），可以秤出幾種不同重量的物體？

解析：是組合問題，分三類用1個砝碼、2個砝碼、3個砝碼，C（3，1）+C（3，2）+C（3，3）=3+3+1=7（種）。

由于排列組合問題在生活中經常見到，在小學階段很多問題要用到這方面的知識，所以在小學階段掌握一些排列組合的知識對我們方便解決一些數學問題大有幫助，而在分析解決的過程中培養了學生的推理能力和有順序地、全面地思考問題的能力。

參考文獻：

[1]課程教材研究所，小學數學課程教材研究中心.數學 [M]，北京：人民教育出版社出版，2004.6，第一版 .

[2]人民教育出版社中學數學室.數學 [M].北京：人民教育出版社出版，2003.6，第一版.第二冊.

[3]張定強，呂世虎.高中新課程內容解析[M].北京：首都師范大學出版社，2004.9，第一版.

[4]傅龍驤.數學奧林匹克[M].蘭州：蘭州大學出版社，2005.2，第一版.

[5]魏有德.數學奧林匹克初級讀本[M].成都：四川大學出版社，2000.6，第三版.