全國高考基礎題訓練卷

江蘇 王懷學

湖北 廖慶偉

遼寧 隋 清

湖北 廖慶偉

湖北 廖慶偉

遼寧 隋 清

遼寧 隋 清

甘肅 文貴雙

湖北 廖慶偉

甘肅 文貴雙

湖北 廖慶偉

江蘇 李紅艷

全國高考基礎題訓練卷

訓練卷一（新課標Ⅰ）

江蘇 王懷學

湖北 廖慶偉

一、選擇題

4．兩個袋中都裝有6張分別寫有數字0，1，2，3，4，5的卡片，現從每個袋中各任取一張卡片，則兩張卡片上數字之和等于7的概率為（ ）

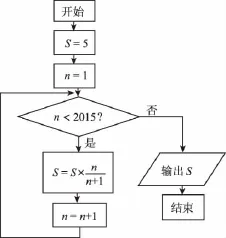
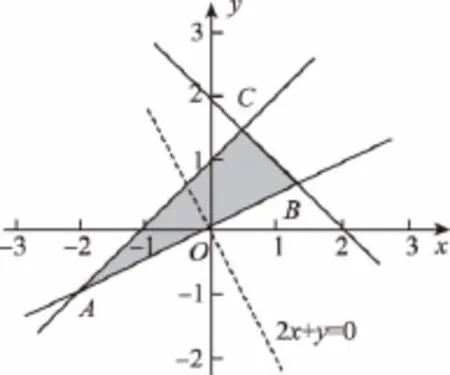
8．如圖所示的程序框圖，輸出S的值是（ ）

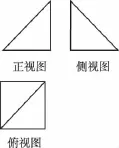
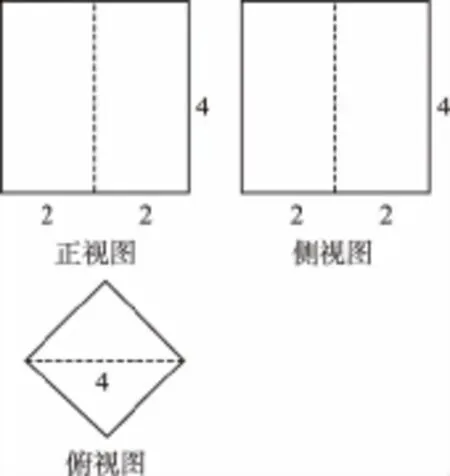
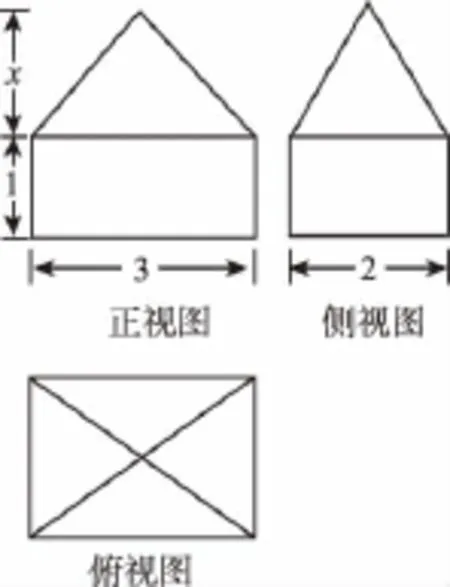
9．如圖，一個幾何體的三視圖（正視圖、側視圖和俯視圖）為兩個等腰直角三角形和一個邊長為2的正方形，則其外接球的體積為（ ）

10．過拋物線C：x2＝2y的焦點F的直線l交拋物線C于A、B兩點，若拋物線C在點A處切線的斜率為1，則△OAB的面積為（ ）

二、填空題

14．某同學騎電動車以24km／h的速度沿正北方向的公路行駛，在點A處測得電視塔S在電動車的北偏東30°方向上，15min后到點B處，測得電視塔S在電動車的北偏東75°方向上，則點B與電視塔的距離是km．

三、解答題

15．已知數列｛an｝的前n項和為Sn，2Sn－an＋1＝2Sn－1＋an－1（n≥2，n∈N＊）．

（1）證明：數列｛2an－1｝是等差數列；

（2）設a1＝1，a3＝3，bn＝，求數列｛bn｝的前n項和Tn．

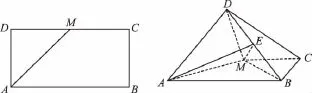
（1）求證：AD⊥BM；

（2）若點E是線段DB上的一動點，問點E在何位置時，三棱錐E—ADM的體積與四棱錐D—ABCM的體積之比為1∶3．

【參考答案與提示】

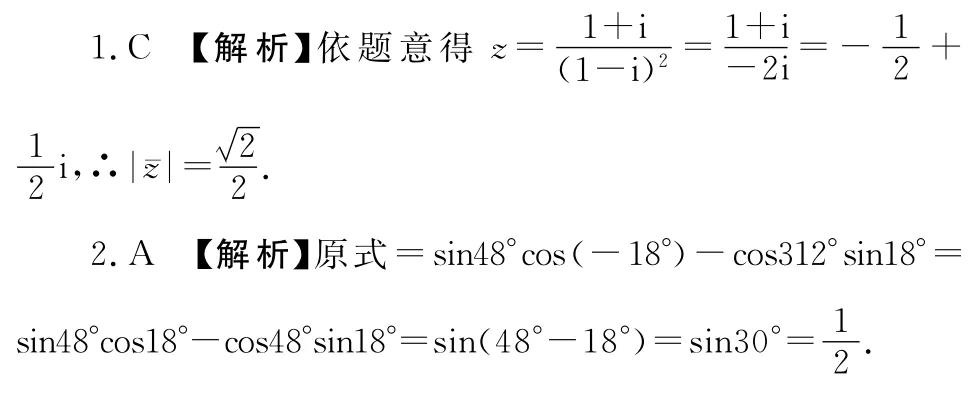
3．D

4．C 【解析】依題意，取出的兩張卡片上數字之和等于7，有2和5，5和2，3和4，4和3四種情況．基本事件的總數是6×6＝36種，故兩張卡片上數字之和等于7的概率為，選C．

9．D 【解析】原幾何體為有一條側棱垂直于底面的四棱錐，且底面是邊長為2的正方形，垂直于底面的側棱長也為1，所以該幾何體可以補形為一個棱長為2的正方體，其外接球就是這個正方體的外接球，直徑為正方體的對角線長，即外接球的半徑為，故外接球的體積為

訓練卷二（新課標Ⅰ）

遼寧 隋 清

湖北 廖慶偉

一、選擇題

1．已知集合A＝｛x｜x2－x－2≤0｝，B＝｛x｜2x＜1｝，則A∩B＝（ ）

A．（1，2） B．（1，2］

C．［－1，0）D．（－1，0）

2．已知i是虛數單位，設復數z1＝1＋i，z2＝1＋2i，則在復平面內對應的點在（ ）

A．第一象限 B．第二象限

C．第三象限 D．第四象限

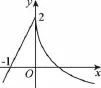
3．下列函數中，在（0，＋∞）上單調遞增的偶函數是（ ）

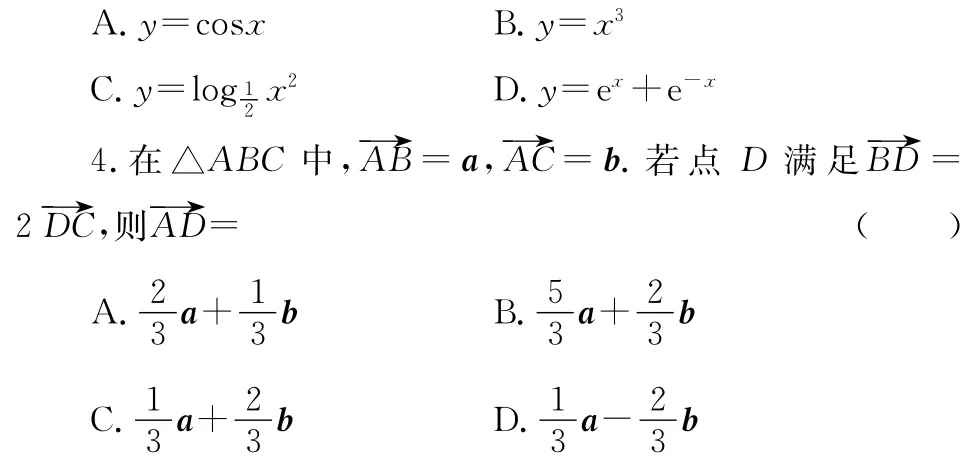
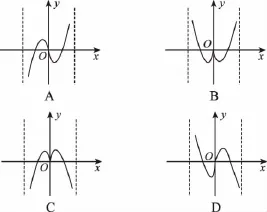
6．執(zhí)行圖中的程序框圖（其中［x］表示不超過x的最大整數），則輸出的S值為（ ）

A．4B．5C．6D．7

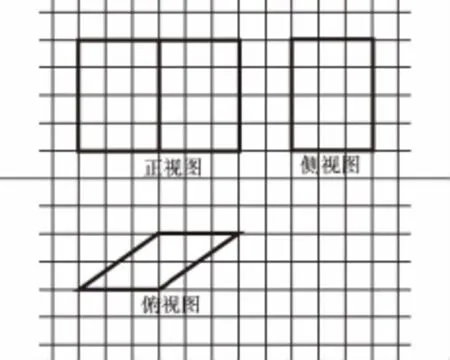
7．下圖是一個幾何體的三視圖，圖中每個小方格的邊長為1，則該幾何體的表面積為（ ）

9．若拋物線y2＝2px（p＞0）上一點P（3，y0）到其準線的距離為5，則拋物線的標準方程為（ ）

A．y2＝32x B．y2＝8x C．y2＝4x D．y2＝2x

10．已知函數f（x）＝x3＋3ax2＋3bx＋c在x＝2處有極值，其圖象在x＝1處的切線平行于直線6x＋2y＋5＝0，則f（x）的極大值與極小值之差為（ ）

A．4B．2C．0D．－3

二、填空題

12．學校有3個研究性學習小組，甲、乙兩名同學各自參加其中1個小組，每位同學參加各個小組的可能性相同，則這兩位同學不參加同一個小組的概率為________．

14．已知△ABC的角A、B、C所對的邊分別是a、b、c，設向量m＝（a，b），p＝（1，1）．若m·p＝4，邊長c＝2，則△ABC的面積的最大值為________．

三、解答題

15．設數列｛an｝的前n項和Sn滿足：Sn＝nan－2n（n－1），等比數列｛bn｝的前n項和為Tn，公比為a1，且T5＝T3＋2b5．

（1）求數列｛an｝的通項公式；

16．我校高三（15）班有學生45人，為了解本班學生喜愛唱歌是否與性別有關，班主任對全班45人進行了問卷調查得到了如下的2×2列聯(lián)表：

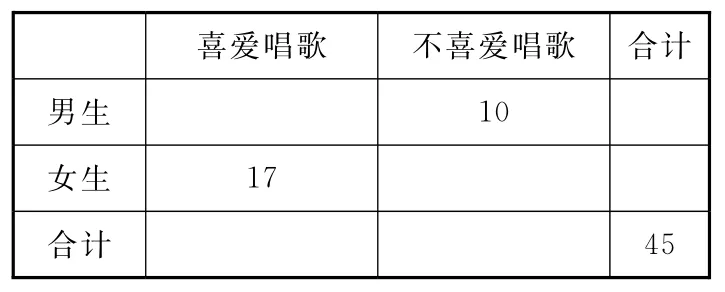
已知在全班45人中隨機抽取1人，抽到不喜愛唱歌的學生的概率為

（1）請將上面的2×2列聯(lián)表補充完整；

（2）你是否有95%的把握認為喜愛打籃球與性別有關？說明你的理由；

下面的臨界值表供參考：

【參考答案與提示】

1．C 【解析】由題意得A＝［－1，2］，B＝（－∞，0），∴A∩B＝［－1，0）．

6．D 【解析】每次循環(huán)的結果分別為：n＝0，S＝0；n＝1，S＝1；n＝2，S＝1＋1＝2；n＝3，S＝2＋1＝3；n＝4，S＝3＋2＝5；n＝5，S＝5＋2＝7，這時n＞4，輸出S＝7．

7．C 【解析】由三視圖知，該幾何體是直平行六面體，底面是邊長為，高為2的平行四邊形，高為4．∴直平行六面體的表面積為

8．A 【解析】不等式表示的可行域如圖所示，把目標函數z＝2x＋y轉化為y＝－2x＋z表示的是斜率為－2，截距為z的平行直線系，當截距最小時，z最小，當直線z＝2x＋y經過點B時，z最小，

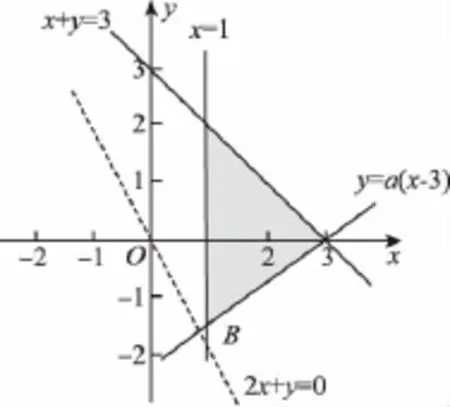
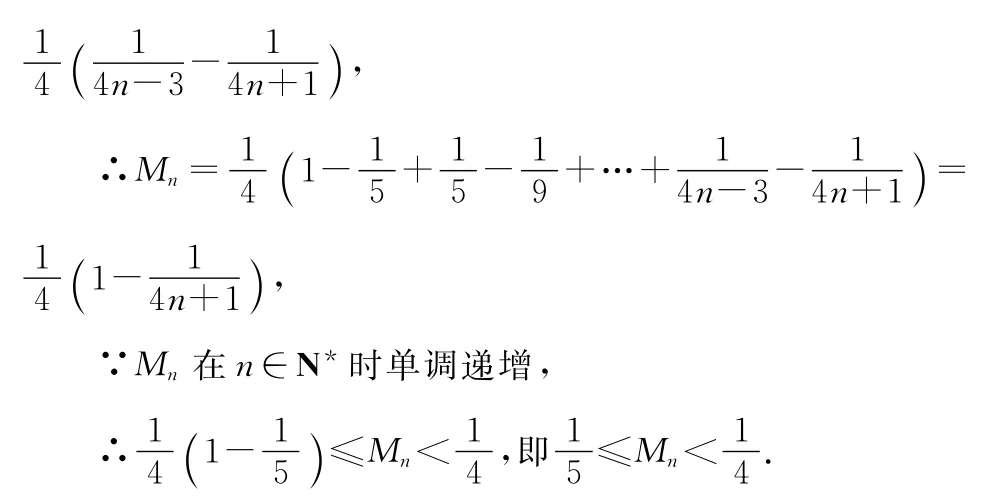
16．【解析】（1）∵在全班45人中隨機抽取1人，抽到喜愛唱歌的學生的概率為

列聯(lián)表補充如下：

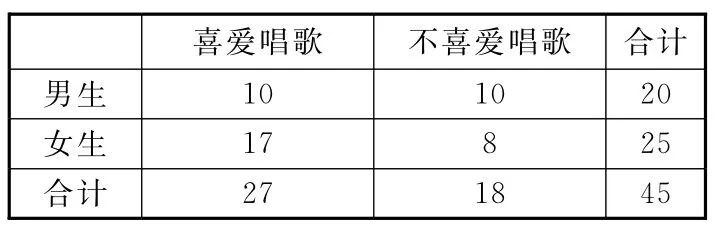
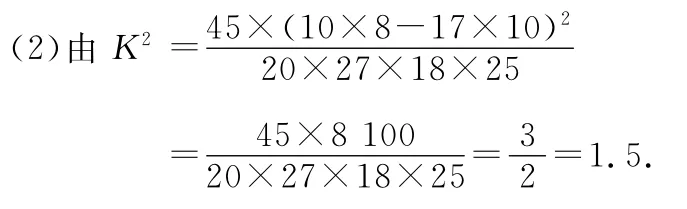
∵1．5＞1．323，∴有75%的把握認為喜愛唱歌與性別有關．

訓練卷三（新課標Ⅰ）

湖北 廖慶偉

遼寧 隋 清

一、選擇題

（ ）

A．（0，2） B．［0，2］ C．｛0，1，2｝D．｛0，2｝

2．已知i是虛數單位，設復數z1＝1＋i，z2＝1＋2i，則在復平面內對應的點在（ ）

A．第一象限 B．第二象限

C．第三象限D．第四象限

4．已知各項均為正數的等比數列｛an｝，a1a2a3＝8，a7a8a9＝27，則a4a5a6＝（ ）

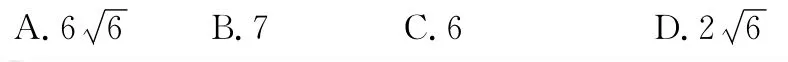
A．10B．15C．20D．40

7．如圖是某程序框圖，則程序運行后輸出的結果是（ ）

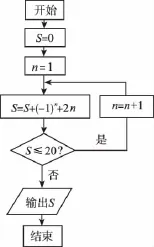
A．6B．32C．34D．101

10．一個幾何體的三視圖如圖，則原幾何體的外接球的表面積為（ ）

A．20B．32πC．16πD．40π

二、填空題

三、解答題

15．已知△ABC中，a，b，c分別為角A，B，C所對的邊，3bcos A＝ccos A＋acosC．

（1）求tanA的值；

16．已知圓心為C的圓，滿足下列條件：圓心C位于x軸正半軸上，與直線3x－4y＋7＝0相切，且被y軸截得的弦長為，圓C的面積小于13．

（1）求圓C的標準方程；

（2）設過點M（0，3）的直線l與圓C交于不同的兩點A，B，以OA，OB為鄰邊作平行四邊形OADB．是否存在這樣的直線l，使得直線OD與MC恰好平行？如果存在，求出l的方程；若不存在請說明理由．

【參考答案與提示】

7．C 【解析】列表分析：

運行次數_______S值____S≤20？__n值___1 __S＝0－1＋2＝1 _______是__n＝2 ___2 __S＝1＋1＋4＝6 _______是__n＝3 ___3 _S＝6－1＋6＝11 _______是n＝4 ____4 S＝11＋1＋22＝34 __否，輸出S＝34

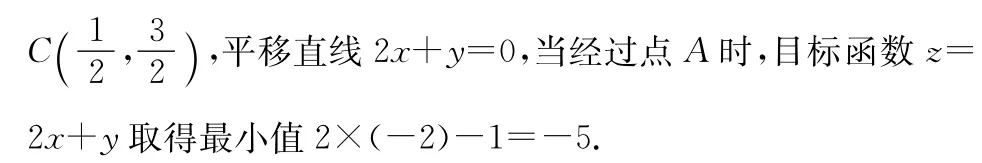
訓練卷四（新課標Ⅰ）

遼寧 隋 清

甘肅 文貴雙

一、選擇題

1．已知集合A＝｛x｜x2－3x－4≥0｝，B＝｛x｜－2≤x＜4｝，則A∩B＝（ ）

A．［－2，－1］ B．［－1，4）

C．［－1，1］D．［1，4）

A．1＋i B．1－i

C．i D．－i

A．f（x）g（x）是偶函數

B．｜f（x）｜g（x）是奇函數

C．f（x）｜g（x）｜是奇函數

D．｜f（x）g（x）｜是奇函數

4．已知F是雙曲線C：x2－my2＝2 m（m＞0）的一個焦點，則點F到C的一條漸近線的距離為（ ）

A．3 B．0

6．將4個不同的微信內容隨機發(fā)給2個不同的好朋友，則這兩個好朋友都接到微信的概率為（ ）

8．執(zhí)行如圖所示的程序框圖，若輸入n的值為8，則輸出S的值為（ ）

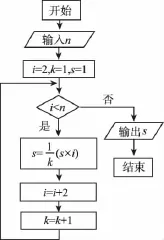
A．4 B．8 C．10 D．12

10．已知拋物線C：y2＝8x的焦點為F，準線為l，P是l上一點，直線PF與C相交，交點為Q、H，若，則｜QH｜＝（ ）

A．7B．6

C．5D．4

二、填空題

11．（x－y）（x＋y）8的展開式中x3y6的系數為________（用數字填寫答案）．

，則a與b的夾角為________．

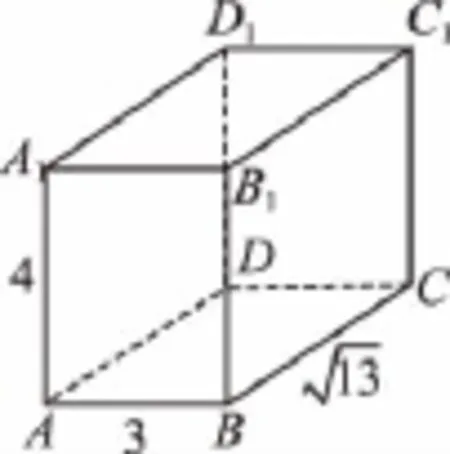
13．設三棱柱側棱垂直于底面，底面三角形為等腰三角形，兩腰長為a，頂角為120°，側棱長為a，所有頂點均在同一個球面上，則此球的表面積為________．

14．已知a，b，c分別為△ABC的三個內角A，B，C的對邊，a＝2，且（2＋b）（sinA－sinB）＝（c－b）sinC，則△ABC周長的最大值為________．

三、解答題

15．設數列｛an｝滿足

（Ⅰ）求數列｛an｝的通項公式；

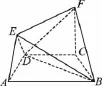
16．在如圖所示的幾何體中，四邊形ABCD是等腰梯形，AB∥CD，∠DAB＝60°，FC⊥平面ABCD，AE⊥BD，CB＝CD＝CF．

（Ⅰ）求證BD⊥平面AED；

（Ⅱ）求二面角F—BD—C的余弦值．

【參考答案與提示】

1．A 【解析】A＝｛x｜x2－3x－4≥0｝＝（－∞，－1］∪［4，＋∞），所以A∩B＝［－2，－1］．

3．C 【解析】f（x）是奇函數，g（x）是偶函數，所以｜f（x）｜是偶函數，由函數的奇偶性定義可得C．

4．A 【解析】雙曲線C的焦點F到C的一條漸近線的距離為

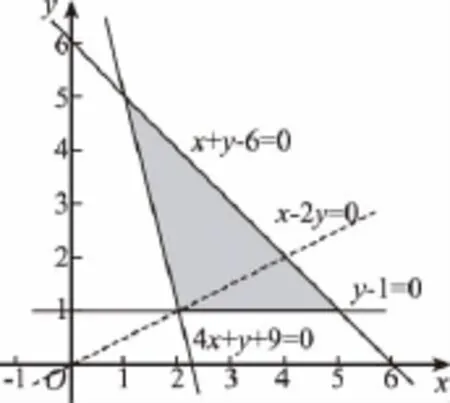
5．A 【解析】畫出可行域知，該區(qū)域是由點A（5，1），B（2，1），C（1，5）所圍成的三角形區(qū)域（包括邊界），直線z＝ x－2y在y軸上的截距為，斜率為，調整直線位置，易得在點A（5，1）取到最大值z＝3．

6．D 【解析】4個不同的微信內容隨機發(fā)給2個不同的好朋友共有16種情況，如果4個微信只發(fā)給一個人，有2種方法，所以兩個好朋友都有接到微信的概率

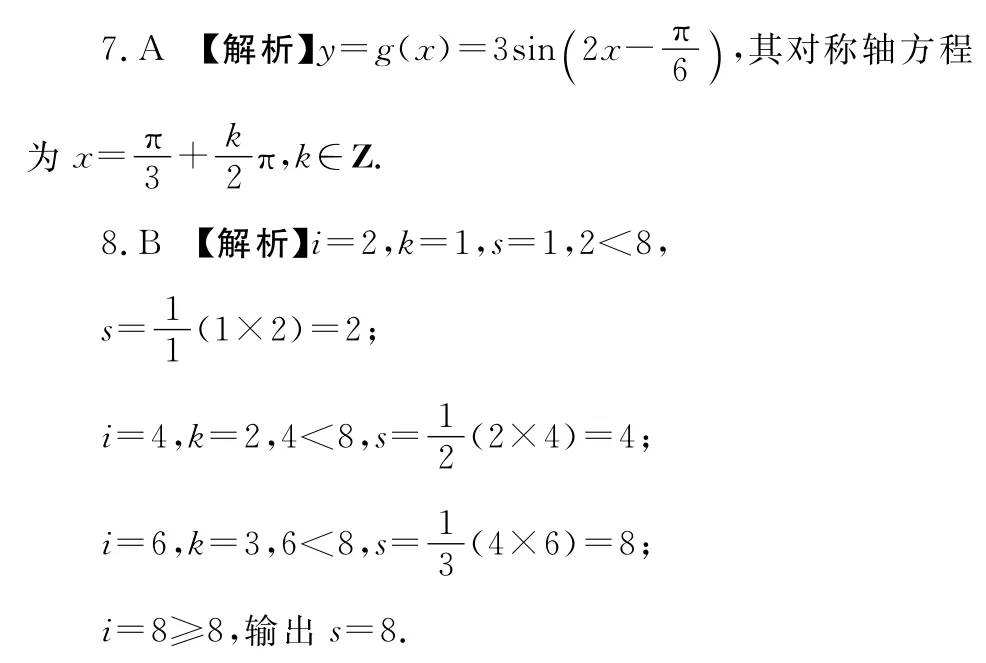
9．B 【解析】切化弦，分式變整式，可得cos（α－β）＝sinα，因為，所以或（舍去），所以選B．

10．B 【解析】由已知得，Q在P和F之間，直線與拋物線的另一個交點為H，設Q到準線的距離為d，則QF＝d，PQ＝3d，由三角形相似可得d＝3，再設H到準線的距離為m，則HF＝m，再由三角形相似可得m＝6．

11．－28 【解析】原式＝x（x＋y）8－y（x＋y）8，所以x3y6的系數為C28－C38＝－28．

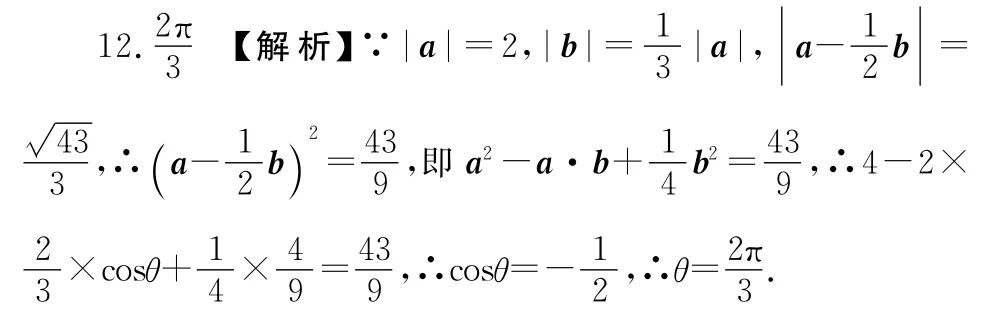
13．5πa2【解析】底面三角形中，由正弦定理可知其外接圓半徑為a，再由勾股定理可算出三棱柱的外接球半徑為，所以球的表面積5πa2．

14．6 【解析】將a＝2代入（2＋b）（sinA－sinB）＝（c－b） sinC中，（a＋b）（sinA－sinB）＝（c－b）sinC，可以算出角再由余弦定理和均值不等式，可以求出周長的最大值為6．

16．【解析】（Ⅰ）證明：因為四邊形ABCD為等腰梯形，AB∥CD，∠DAB＝60°，所以∠ADC＝∠BCD＝120°，又CB＝CD，所以∠CDB＝30°

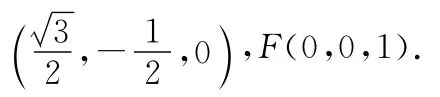
訓練卷五（新課標Ⅱ）

湖北 廖慶偉

甘肅 文貴雙

一、選擇題

1．已知集合M＝｛x｜－2＜x＜3｝，N＝｛x｜2x＋1≤1｝，則M∩（瓓RN）＝（ ）

A．（3，＋∞） B．（－2，－1］

C．（－1，3）D．［－1，3）

2．設向量a＝（－1，2），b＝（m，1），如果向量a＋2b與2a－b平行，那么2a與b的數量積等于（ ）

4．設事件A在每次試驗中發(fā)生的概率相同，且在三次獨立重復試驗中，若事件A至少發(fā)生一次的概率為，則事件A恰好發(fā)生一次的概率為（ ）

5．已知，x∈R，函數f（x）滿足f（－x）＋f（x）＝0，f（x＋2）＋f（x）＝0，當x∈［0，2］時f（x）＝x2，則f（2 015）＝（ ）

A．0B．－1

C．1D．2

6．某程序框圖如圖，該程序運行后輸出的k的值是（ ）

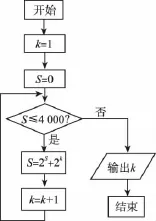
A．2 B．3 C．4 D．5

A．函數g（x）是奇函數

B．函數g（x）在區(qū)間［π，2π］上是增函數

C．函數g（x）的最小正周期為π

A．｛－3，0｝B．｛3，－1｝

C．｛0，1｝D．｛－3，0，1｝

9．在等差數列｛an｝中，a1，a2015為方程x2－10x＋16＝0的兩根，則＝（ ）

A．10B．15

C．20D．40

10．若直線2x＋ay－13＝0（a＞0）與圓x2＋2x＋y2－24＝0相切于P，則直線與兩坐標軸圍成的三角形的面積為（ ）

二、填空題

11．如圖是一個體積為10的空間幾何體的三視圖，則正視圖的面積為________．

三、解答題

15．如圖，圖1網格中每個小正方形的邊長為1，把四邊形ABCD沿EF折成如圖2的形狀，若

（1）證明：平面ABFE⊥平面FCDE；

（2）若CM＝DM，求三棱錐C—BFM的體積．

（1）當a＝1時，求函數f（x）的圖象在點A（－2，f（－2））處的切線方程；

（2）令F（x）＝f（x）－g（x），判斷函數F（x）的極值點．

【參考答案與提示】

1．C 【解析】N＝｛x｜x≤－1｝，瓓RN＝｛x｜x＞－1｝，∴M∩（瓓RN）＝｛x｜－2＜x＜3｝∩｛x｜x＞－1｝＝｛x｜－1＜x＜3｝．

2．C 【解析】a＋2b＝（－1＋2m，4），2a－b＝（－2－m，3），由題意得3（－1＋2m）－4（－2－m）＝0，則

4．A 【解析】假設事件A在每次試驗中發(fā)生說明試驗成功，設每次試驗成功的概率為p，由題意得，事件A發(fā)生的次數X～B（3，p），則有，得，則事件A恰好發(fā)生一次的概率為

5．B 【解析】∵f（x＋2）＋f（x）＝0，∴f（x＋4）＝f（x），即函數f（x）是周期為4的函數，∴f（2 015）＝f（4×504－1）＝f（－1），∵f（－x）＋f（x）＝0，∴f（－1）＝－f（1），x∈［0，2］時，

f（x）＝x2，∴f（1）＝1，∴f（2 015）＝－1，選B．

6．C 【解析】第一次循環(huán)，S＝0，k＝1；第二次循環(huán)，S＝20＋21＝3，k＝2；第三次循環(huán)，S＝23＋22＝12，k＝3；第四次循環(huán)，S＝212＋23＝4 104＞4 000，k＝4，終止循環(huán)，輸出k＝4．

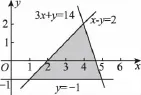
8．B 【解析】作出不等式組所表示的平面區(qū)域，如圖所示．易知直線z＝ax＋y與x－y＝2或3x＋y＝14平行時取得最大值的最優(yōu)解有無窮多個，即－a＝1或－a＝－3，∴a＝－1或a＝3．

10．D 【解析】由圓x2＋2x＋y2－24＝0得（x＋1）2＋y2＝52，又∴直線2x＋ay－13＝0與圓相切，由點到直線的距離公式得，解得，∵a＞0，∴直線方程為13＝0，令x＝0得，令y＝0得，∴所求三角形的面積為

11．6 【解析】根據給定的三視圖可知，該幾何體對應的直觀圖是一個長方體和四棱錐的組合體，∴幾何體的體積，解得x＝2．

15．【解析】（1）證明：由圖1知，AE⊥EF，DE⊥EF，AE＝DE＝4．在圖2△AED中，AE＝DE＝4，

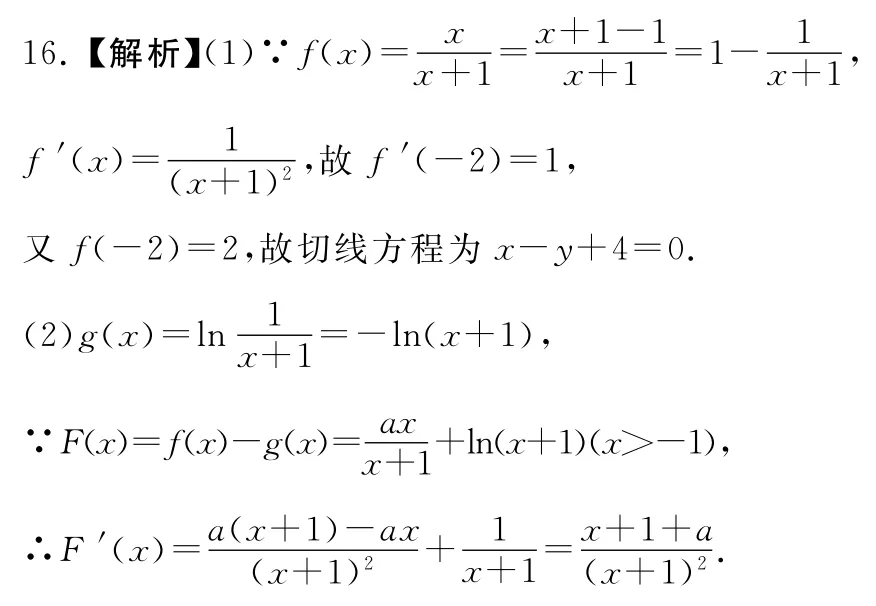
①當a≥0時，因為x＞－1，∴f′（x）＞0，此時函數F（x）在（－1，＋∞）上單調遞增，無極值點；

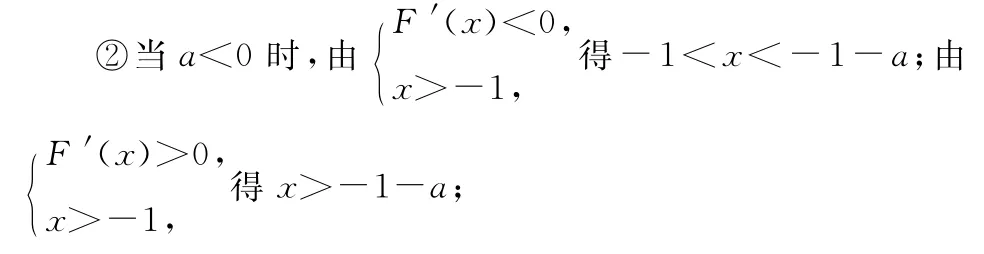
故函數F（x）在（－1，－1－a）單調遞減，在（－1－a，＋∞）上單調遞增，

故F（x）有極小值點x＝－1－a，無極大值點．

綜上所述，當a≥0時，F（x）無極值點；當a＜0時，F（x）有極小值點x＝－1－a，無極大值點．

訓練卷六（新課標Ⅱ）

湖北 廖慶偉

江蘇 李紅艷

一、選擇題

1．已知集合A＝｛x｜0≤x＜2 016｝，B＝｛x｜－3＜x≤5｝，則集合A∪B＝（ ）

A．（－2，0） B．（0，5］

C．（－3，2 016］D．［5，2 016］

A．1 B．2 C．－1 D．－2

3．某程序框圖如圖所示，若輸入x的值為4，則輸出x的值是（ ）

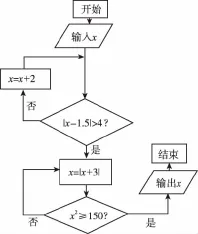
A．16 B．15 C．14 D．13

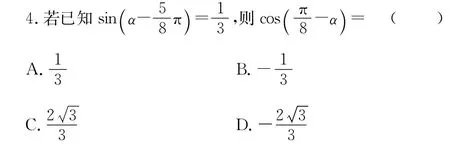
5．已知向量a與向量b的夾角為120°，若（a＋b）⊥（a－2b），｜a｜＝2，則向量b在a上的投影為（ ）

7．2015年9月3日，中國人民抗日戰(zhàn)爭勝利紀念日閱兵式中，有7架飛機，拉出7道彩帶，如果拉出的彩帶的顏色是紅色與黃色必相鄰的，則飛機拉出的彩帶的顏色不同排序方法的數量是（ ）

A．120 B．144

C．480 D．1 440

A．0B．1

C．2D．4

10．已知拋物線y2＝8px（p＞0）與雙曲線（a＞0）有相同的焦點F，點A是兩曲線的一個交點，且△OAF是等邊三角形，則雙曲線的離心率為（ ）

二、填空題

11．某校對全校男女學生共1 600名進行健康調查，選用分層抽樣法抽取一個容量為200的樣本．已知女生比男生少抽了10人，則該校的女生人數是________人．

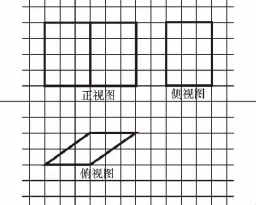
12．下圖是一個幾何體的三視圖，圖中每個小方格的邊長為1，則該幾何體的表面積為________．

13．第24屆冬季奧林匹克運動會，簡稱“北京冬奧會”，將在2022年02月04日至20日在中華人民共和國北京市和張家口市聯(lián)合舉行．現對50名冬奧會大項志愿者負責人進行培訓．這50名志愿者中既會英語又會俄語的進行了調查，統(tǒng)計數據如下表所示：

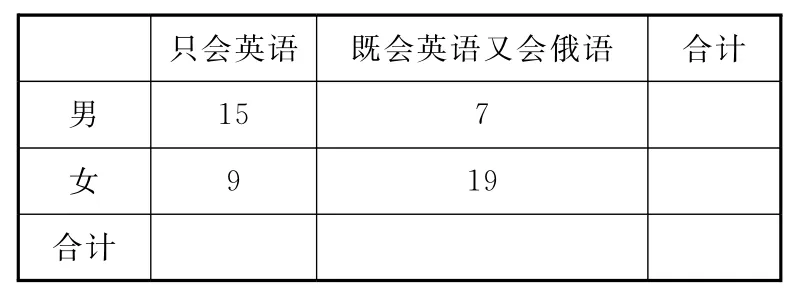
只會英語既會英語又會俄語合計男____15 __________7女9 19 __合計

試運用獨立性檢驗的思想方法分析：志愿者既會英語又會俄語與只會英語與性別_________關系．（填“有”或“無”）

參考數據：

P（K2≥k）0．15 _0．10 0．05 0．025 0．010 0．005 0．001 ____k 2．07 2．71 3．84 5．02 6．64 7．88 10．83

三、解答題

15．如圖，△ABC中，三個內角B、A、C成等差數列，且AC＝10，BC＝15．

（1）求△ABC的面積；

（2）已知平面直角坐標系xOy，點D（10，0），若函數的圖象經過A、C、B三點，且A、B為f（x）的圖象與x軸相鄰的兩個交點，求f（x）的解析式．

16．已知函數f（x）＝x2－ax，g（x）＝mx＋nlnx．函數f（x）在點（1，f（1））處的切線的斜率為1，函數在x＝2處取到極小值2－2ln2．

（1）求函數f（x），g（x）的解析式；

（2）已知不等式f（x）＋g（x）≥x2－m（x－1）對任意的x∈（0，1］恒成立，求實數m的取值范圍．

【參考答案與提示】

1．C 【解析】A∪B＝｛x｜－3＜x≤2 016｝．

3．B 【解析】程序運行如下：輸入x＝4，判斷｜4－1．5｜＝2．5＜4，執(zhí)行x＝4＋2＝6；

輸入x＝6，執(zhí)行｜6－1．5｜＝4．5＞4，執(zhí)行x＝6＋3＝9，判斷92＝81＜150；

x＝9＋3＝12，判斷122＝144＜150；x＝12＋3＝15，判斷152＝225＞150．輸出x＝15．

7．D 【解析】依題意拉出的彩帶的顏色是紅色與黃色必相鄰的，共有6A22種不同的排法，其他顏色沒有要求，∴共有6A22A55＝1 440種不同排法．

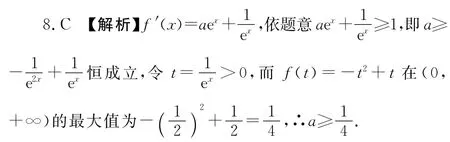
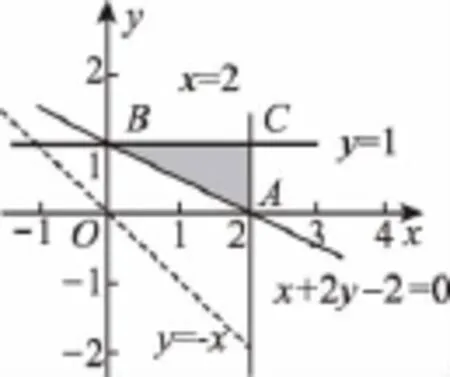
9．B 【解析】不等式組表示的平面區(qū)域如圖中的△ABC，要求｜x＋y｜的最小值，即平移直線y＝－x，使得經過點B時最小，易求得B（0，1），∴所求最小值為0＋1＝1，選B．

11．760 【解析】由題可知，容量為200的樣本中女生比男生少抽了10人，于是樣本中女生抽取了95人，設該校女生的人數為x人，則有，解得x＝760，即該校女生有760人．

13．有 【解析】2×2列聯(lián)表如下：

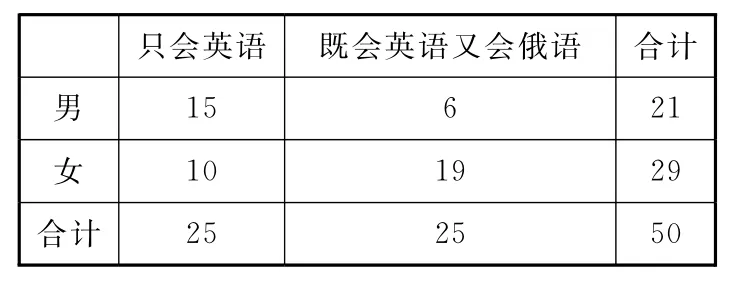
只會英語既會英語又會俄語合計男___15 _________6 _21女____10 _________19 _29合計25 25 50_

由K2統(tǒng)計量的計算公式得

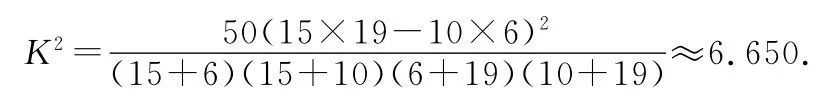
由于6．650＞6．64，∴有99%的把握認為志愿者既會英語又會俄語與只會英語與性別有關系．

若函數h（x）＝f（x）－g（x）有四個零點，則函數f（x）與g（x）的圖象有四個交點．