數學課堂教學培養學生學習方法初探

孫桂媛（遼寧省莊河市第三十一初級中學）

?

數學課堂教學培養學生學習方法初探

孫桂媛
（遼寧省莊河市第三十一初級中學）

摘要：在數學課堂教學中，教師只有堅持以生為本，針對不同的問題、不同的學生，構建科學合理的學習模式，才能引導學生主動探究、發現、提出問題，解決問題，進而掌握方法，施展才華，發揮潛能，成為學習的主人，提升個人的素質，達到極佳的學習效果。

關鍵詞：數學課堂；主動性；歸納性

一、培養學生主動學習意識

實踐證明，學生對自己主動學會的知識掌握得比較牢固、深刻、透徹。

二、培養學生綜合運用知識能力

在教學實踐中，我發現綜合運用知識會大大提高知識的連貫性，培養學生一題多解的能力，同時也是復習鞏固歸納知識的最好方法，讓學習過程變得有氣息、有生活、有成就感。在初三第一輪復習三角形中位線定理時，教材中有這樣一道習題：如下圖所示，A，B兩點被池塘隔開，在AB外選一點C，連接AC和BC，怎樣測出A、B兩點間的距離？根據是什么？

甲說：分別取AC、BC的中點D，E，連接DE，測出DE的長度，則AB兩點的距離就是2DE長，根據三角形中位線定理。

甲說完后，我又提示，利用三角形全等的知識和相似的知識能否解決。

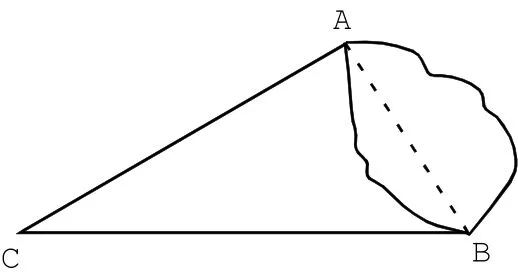
乙說：延長AC到D，使CD=AC，延長BC到E，使CE=BC，連接DE，根據SAS可證△ABC≌△DEC，從而AB=DE，測出DE的長度就是A、B兩點間的距離。

接著丙又提出了可用相似解決AB間距離問題的具體方法。

最后我讓小組討論，尋找其他解決方法，學生又提出了用解直角三角形的方法。一道簡單的練習題，綜合了三角形中位線定理、全等、相似、解直角三角形等諸多知識，既使學生的思維打開，又拓寬了解題的方法，避免了解決問題的單一性、片面性、是復習、提升的最佳方法。

三、培養學生分析問題和解決問題的能力與方法

我從事數學教學三十多年，每年中考或高考結束，總體上對數學這一科反饋的聲音是“難”。實際上“難”在學生找不到解決問題的方法上。故培養學生分析問題和解決問題的能力是打開“難”的一把鑰匙，以下幾種方法是我在教學中常用的方法。

1.類比法。如，七年級上學期學生已學了線段的中點和角的平分線的定義與性質。在教學過程中，我在講角的平分線的定義與性質時就聯想線段的中點定義和性質來解決，在八年級上學期講三角形中線的性質就聯想線段中點的性質，講三角形角平分線的性質就聯想角平分線的性質。

2.逆向思維法。由果至因，這是幾何證明中常用的方法，即逆推命題的推理過程來尋求解決問題的突破口。看下面這道幾何題：如下圖所示，CE是△ABC中∠ACB的平分線，CF是∠ACB外角∠BCD的平分線，MN∥AD交CE于M，交CF于N，MN交BC 于O，當O運動到什么位置時，且△ABC滿足什么條件時，四邊形BMCN是正方形，為什么？這道題對于中等生和中等生以下學生在短時間內要想解決這個問題，會覺得無處下手，其實解決這個問題方法之一就是逆向思維。若四邊形BMCN是正方形，則必有：（1）OB=OC=OM =ON：（2）∠MCN=90°；（3）BC⊥MN。上述幾個結論，OM=OC=ON及（2）可由已知得出，只需讓OC=OB和BC⊥MN即可。由OC=OB可知，O運動到線段BC中點處；由MN∥AD，BC⊥MN可得到∠ACB=90°，即△ABC滿足AC⊥BC，從而使問題得到解決。

課堂教學學生是主體，教師應充分尊重每個學生，但不能忽視教師的引導作用及學習方法的培養與選擇。因為學生看待問題、提出問題、解決問題的眼光與途徑畢竟不成熟到位。故教師要恰到好處地給予引導，其自身的潛能便可充分挖掘施展，學生學到的不只是一堂課的知識，而是終身的學習方法，從而達到最佳的教學效果。

·編輯韓曉