淺談如何提高初中數學概念教學的有效性

林婉蓮

[摘 要] 在教學過程中，如何把握數學課堂上的概念教學，如何引導學生加強對概念的理解，如何提高數學概念教學的有效性，成為擺在所有初中數學教師面前的一個難題，本文就此問題結合教學經驗談幾點認識.

[關鍵詞] 初中數學；概念；有效性

初中數學概念在數學教學中占有相當重要的地位，可以說是數學的生命線. 其實，縱觀人民教育出版社初中三年的學習內容可以清楚地看到，每一章都是圍繞一個或幾個概念展開的，因此，抓住概念、加強對概念的理解與應用是學生數學學習的核心內容；另一方面，數學概念是高度概括的，十分抽象，對初中生來說有些顯得難以理解. 但據筆者的觀察，在概念教學過程中，更多的教師是匆匆忙忙地講完概念，然后開始大量做題，忽視了概念的生成過程；對于學生來說，更多的學生對概念的學習沒有任何想法，他們對數學學習的理解就是完成教師布置的作業. 這樣“填鴨式”教學方式的結果可想而知，尤其是像數學這種需要思維的科目，因此，很多學生感嘆數學難懂，教師們則覺得學生一代不如一代. 這已成為數學教學的現狀.

從近幾年的中考數學試卷來看，考查方式已經逐漸從以往知識掌握情況的檢閱轉變為對能力的考查. 試卷不僅要檢查學生對基本知識的掌握情況以及基本技能，更要檢閱學生各項數學能力的提升的程度. 學生不僅要會應用已有的知識，更要學會分析問題、解決問題，而能力的提升絕對不是“填鴨式”教學所能實現的，所以，在日常教學中，概念教學作為數學教學的核心，如何把握數學課堂上的概念教學，如何引導學生加強對概念的理解，如何提高數學課堂教學的有效性，從而促進學生數學能力的提升，是擺在所有初中數學教師面前的一大難題.

筆者仔細研讀了人民教育出版社的初中教材發現：初中數學概念多，基本上可以分為兩大類，一類是描述性，往往用“形如”“像這樣”的文字表示；一類是定義式，語言表述嚴謹，用詞規范. 描述性的概念表達得清楚明了，但是概括性不強，需要教師加以引導、解釋，定義式概念言簡意賅，抽象程度大大加強，這類概念需要教師加以剖析. 總之，對概念的理解需深入，需要教師的指導. 為解決這一問題，筆者結合自身教學經驗，總結出了概念教學的“四步法”：“悟”“探”“剖”“拓”，下面進行詳細闡述.

第一步：“悟”，即情景引入，感

悟概念

《全日制義務教育數學課程標準（2011版）》指出：學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程. 也就是說，知識不能“填鴨式”地交給學生，而應通過觀察、實驗、猜測、計算、推理、驗證等各種方法，讓學生充分感知知識的發生、發展、形成過程. 因此，概念的引入應該是一個自然而然、水到渠成的過程. 初中生由于年齡還小，見識有限，對于復雜的數學概念理解不到位，因此，在教學中，教師可以借助各種手段使數學概念生活化，讓學生容易理解、接受. 借助情景，引入概念，是教學中經常采用的一種手段.

教師選用的情景，可以來自課本. 目前大家所使用的人教版教材在這點上做得比較好，比如，九年級上冊“直線與圓的位置關系”引入部分，課本就提供了兩個情景. 情景1：把太陽看成一個圓，地平線看成一條直線，在太陽升起的過程中，太陽和地平線會有幾種位置關系？由此你能得出直線和圓的位置關系嗎？利用這個情景，教師可以把它做成動畫，利用動畫的演示讓學生直觀地感知直線與圓的位置關系. 在此基礎上，課本又提供了情景2：在紙上畫一條直線，把鑰匙環看作一個圓，在紙上移動鑰匙環，直觀感知在移動過程中直線和圓的交點個數的變化. 這兩個情景很好地展示了直線與圓的幾種位置關系，學生能感悟到直線與圓的位置關系. 在此基礎上讓學生學習直線與圓的位置關系就顯得自然而然.

教師選用的情景還可以根據上課的需要選自其他材料. 比如，講授“有理數的乘方”時，教師可以選用這樣一個情景進行導入：請同學們拿出事先準備好的一張白紙，對折1次、對折2次、對折3次 ……讓學生邊操作邊計算邊記錄，從而感知紙張的層數與對折次數的關系——每多折一次，就應該多乘一個2. 那么，多個2相乘，怎么表示更簡潔呢？從而自然而然地引入乘方的概念. 通過動手操作和計算，學生能直觀地感知概念的形成過程，這有利于學生對乘方的學習. 此外，情景的引入還可以是模型（立體圖形的認識），可以是與內容相呼應的故事，也可以是前面所學的內容. 總之，在教學過程中，教師應合理地選用各種情景導入，以激發學生學習數學的興趣，從而達到較好的學習效果.

第二步：“探”，即探究思考，形

成概念

概念給出后，教師應引導學生探究概念的內涵及外延，研究概念的本質，理解概念中的關鍵詞. 人教版第21章第一課時中二次根式的概念就是一個描述性的概念，課本在給出四道填空題且學生完成后得到這樣一句概括， 概念是很直觀地給出了，但學生如何理解二次根式的概念，如何把握二次根式概念的本質卻需要教師的點撥. 教師可以這樣引導學生理解：（1）首先提出二次根式的基本要求，即必須有根號，被開方數是非負數，且整個根號下的表達式作為被開方數. （2）講解二次根式的來源. 二次根式是建立在學生之前所學的平方根、算術平方根以及平方和開平方這些知識的基礎之上的，而且平方根和算術平方根的被開方數均是非負數. （3）闡述二次根式的范圍擴大了，即二次根式的被開方數擴展到了含有字母表示的代數式，這就是數到式的一個飛躍，同時也為后面二次根式性質的研究打下了堅實的基礎. 通過對上述三個問題的探究，學生親歷了知識的形成過程，對二次根式概念的理解也能達到一定的水平，這就為下面性質的研究做了充分的鋪墊. 教師引導學生探究、思考的過程可以是對文字的分析，也可以是正誤判斷，還可以是小組討論、師生的交流……思維火花的碰撞可以幫助學生更好地理解概念，抓住概念的本質.

第三步：“剖”，即剖析理解，鞏

固概念

心理學原理認為：概念一旦獲得，如不及時鞏固，就會被遺忘. 因此，對學生來說，學習了概念之后，適當的鞏固訓練是必要的. 練習的設置形式是多種多樣的，畫圖題、判斷題、計算題、操作題……教師可以根據所教授的知識合理選用. 筆者在教授平方根的概念時就選用了如下兩組練習.

練習1？搖 求下列各數的平方根：

（1）100？搖 （2）9/16 （3）0.25 （4）0

練習2？搖 判斷下列說法是否正確，并說明理由.

（1）49的平方根是7；

（2）2是4的平方根；

（3）-5是25的平方根；

（4）64的平方根是±8；

（5）-16的平方根是-4.

練習1的設置能再次加強學生對平方根概念的認識，注意一個正數的平方根有兩個，0的平方根是0. 練習2是通過對平方根概念的辨析，強化學生對平方根的理解. 學生完成這組練習后師生共同解答，教師再適時強調，這樣，學生就基本掌握了平方根的概念. 所以，獲得概念后，學生要通過適當的做題完成對概念的理解. 因此，在概念教學過程中，教師要科學地設置題目，且通過學生的答題情況有的放矢地完成點撥、講評，這樣可以達到事半功倍的效果.

第四步：“拓”，即拓展創新，延

伸概念

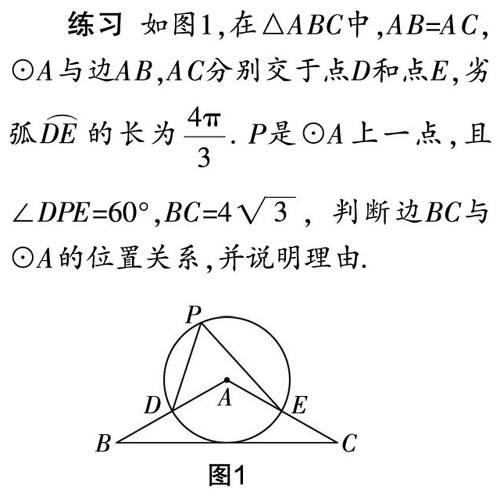
舉一反三、觸類旁通是數學教師最喜歡看到的現象，但是這需要培養. 通過適當的解題，學生才能加深、拓展對概念的認識，而科學合理地設置問題將為學生的學習起到導向作用. 在學生學習完概念之后，教師肯定會通過例題或練習幫助學生鞏固概念，但在此基礎上，教師應特別地設置某些題目，以幫助學生更完整、更深刻地理解和掌握概念的內涵和外延. 如學生學習了“直線與圓的位置關系”后，為了檢測學生對知識的掌握程度，教師可以設置如下一道練習題.

本題涉及的知識有圓周角定理、弧長公式、直線和圓的位置關系的判斷及證明，教師不能簡單、直接地告訴學生如何下筆、怎么求解，而需學生自行分析判斷，找到并計算出圓心A到直線BC的距離d及根據弧長的計算公式求出⊙A的半徑r的大小，再利用d和r的關系得出直線和圓的位置關系. 通過對這類問題的分析與解決，學生的綜合分析能力會得到大大的提高. 這種一題一問的題目正是近幾年廈門中考的熱門題型，能很好地考查學生的綜合分析能力.

通過“四步”教學法的學習，學生能掌握每個概念，并對概念的學習達到一個較高的水平，學習數學會變得比較輕松. 其實，在日常的教學過程中，我們也應不自覺地遵循這個過程進行概念教學. 當然，每一個概念都不是獨立存在的，數學知識之間是緊密聯系的，概念之間是環環相扣的，學習概念時，我們還應抓住知識之間的前后聯系，及時進行歸類整理，活學活用，以求水到渠成. 概念教學是數學課堂的核心，把握住概念教學，才能順利地提高學生的解題能力，也為數學其他知識，包括定理、公式、法則等的學習奠定堅實的基礎.

總之，數學概念是抽象的，是難以理解的，概念的學習需要一個長期的過程. 作為數學教育工作者，我們要遵循教育的規律，在教學實踐中不斷總結、提升自身的教育教學水平，切實提高教學質量.