例談說題的實踐與思考

趙雁泉

摘 要： 從“說課”到“說教學片斷”再到“說題”，教研活動中的“說”的范圍在逐步縮小，卻更有實效。“說題”能夠充分展示教學問題及解決問題的過程，還能夠通過一題多a，一題多變，一題多用揭示數學思維的過程，提高學生解決問題的能力，實現數學課堂輕負高質的效果。教師說題活動能夠促進參與者深入研究題目功能及教學策略，更能踐行有效課堂教學，深入教學的研究和反思，促進教師的專業成長。

關鍵詞： 說題 變式 解決問題 數學思維 創新能力

一、說題的背景

觀察當前的課堂發現，大多數教師仍以“基本知識，基本技能”教學為主，對學生的數學思維和創新能力培養體現不夠。老師們經常埋怨把以前做過、講過的題目，再拿給學生做，學生又不會了。我認為這主要是因為教師在第一次講解這些題目時，對題目功能的挖掘不夠。就題論題，做一題，換一題，使學生的思維跟著跳躍。或者是教師在講解時，只告訴學生怎么做，而沒有呈現為什么這么做的思維過程，導致學生不能真正深入理解知識、方法，缺乏舉一反三，融會貫通。所以，教師研究題目，研究解題教學，提高課堂教學效率是一項重要工作。在遇到新問題時，如何幫助學生找到條件和結論之間的邏輯聯系和橋梁，提高學生分析問題、解決問題的能力，發展數學思維，成了我常常思考的問題。筆者今年有幸參加了杭州市說題比賽、展示活動，我深刻體會到說題能夠促進教師深入挖掘題目功能，研究解題教學策略，從而提高課堂教學質量。教師為了說題會進行深層次備課，突出問題解決的過程，特別是揭示思維展示的過程，歸納問題的典型特性，教學目標從原來的“雙基”到“四基”，體現發展學生的數學思維和創新意識。因此，說題活動是教師改變當前課堂狀況的有效策略之一。

二、說題的定義

在說題之前，先進行解題，解題后，把題目的功能，如何審題、分析、解答、變式、拓展和回顧的思維過程按一定的規律和順序加以敘述，這就是說題。說題時間一般控制在10分鐘左右，不超過15分鐘。說題分為“教師說題”、“教師和學生互動說題”和“學生說題”等。本文主要和大家交流教師說題。在我看來，教師說題更是一種教學教研活動，是促進教師專業發展的有效途徑。教師說題是類似于說課的一種教育教研展示和討論活動，是說課的延續和創新，但是比說課更有針對性，是一種更深層次備課后的展示。

三、說題的作用

說題能促進教師精選題目，并充分研究和挖掘題目功能，完善教學方法，精簡講練，這在一定程度上能夠避免題海戰術，實現教與學的輕負高質。

（一）說題促進教師更深層次的備課，有利于提升教師的學科專業素養。

說題之前，教師要進行一系列的準備工作，如：仔細查閱相關資料，認真學習相關的理論，深刻研究學科知識結構與分類，了解關于問題的來源，研究問題考查的目的，考查的知識、思想方法、解題經驗等。這對于教師把握整個教材體系和課標及對學生的了解的要求更高，思維能力要求更強。說題要求教師理論與實踐的結合，說題能使教師不僅注重結果，更注重過程教學，同時也注重開放式教學。所以說題能有效提高教師的專業能力、教學能力和教研能力，有利于提升教師的學科專業素養。

（二）說題改變課堂教學方式，有助于提高學生解決問題的能力。

說題改變了教師的教學方式，也就改變了學生的學習方式。學生會在教師的潛移默化下，學會用分析法和綜合法分析問題；學會用多種方式解決一個問題，并舉一反三；學會從中知道這道題所包含的理論層面的知識，解決一類問題，一題多用。這樣既能夠培養學生的數學思維，提高學生解決問題的能力，又能夠培養學生敢于探索和創新的精神，提升學生的數學素養。

（三）說題是提高教研活動效率的有效途徑之一。

聽一節課需要40～45分鐘，而說題只需10分鐘左右，所以說題時間短，切口小，但涉及的方面多。一次教研活動可以有多人進行說題展示，所以說題活動是一種有效的教研形式。教師“說”數學問題的解決方法和策略，實質是展示自身的理論功底，數學知識的掌握程度，以及數學方法的理解能力和數學教學的前瞻性。通過課堂的具體實踐，又使教師自身的教育理論得以提煉，也給旁人提供參考，使集體的智慧得以充分發揮。說題者要努力尋求現代教育理論的指導，評價者也要努力尋求說題教師的特色與成功經驗的理論依據，說評雙方圍繞著共同的課題達成共識，達到取長補短、優勢互補的效果，說題者得到反饋，進而改進、提高和完善自己的教學方案；聽者從中得到比較、鑒別和借鑒，得到案例示范和理論滋養兩方面的收益，營造了良好的教研氛圍。

四、說題的實踐

下面以筆者參加杭州市說題展示活動為例，闡述說題的過程。

（一）說題引入。

《數學課程標準解讀》明確指出初中數學課程應當注重發展學生的空間觀念，形成幾何直觀能力，發展合情推理和演繹推理能力。幾何證明是平面幾何中的一個重要問題，它對培養學生邏輯思維能力有很大的作用。下面看一個幾何問題。

（二）題目呈現。

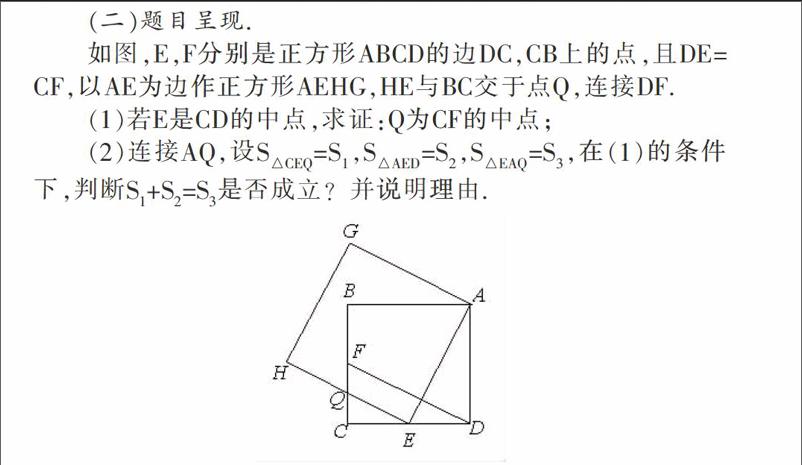
如圖，E，F分別是正方形ABCD的邊DC，CB上的點，且DE=CF，以AE為邊作正方形AEHG，HE與BC交于點Q，連接DF。

（1）若E是CD的中點，求證：Q為CF的中點；

（2）連接AQ，設S=S，S=S，S=S，在（1）的條件下，判斷S+S=S是否成立？并說明理由.

（三）題目賞析。

1。題目來源：本題改編自2015年四川省資陽市中考數學試題的第23題。

2。題目功能：本題注重考查的知識有正方形的性質，全等和相似三角形的判定與性質，勾股定理。本題需要學生具備的基本能力是直觀理解能力、觀察分析能力、邏輯思維能力和問題轉化能力。本題所用的基本思想方法是數形結合思想和轉化化歸思想。本題使學生獲得的基本活動經驗是學會用分析、綜合法找到條件和結論之間的邏輯關聯，善于從復雜圖形中分解出常用圖形。

3。學情分析：學生往往能熟練掌握全等的判定和性質，也能發現相似三角形，但是，多次相似的轉化難度較大，不能很好地與勾股定理結合，轉化綜合分析能力欠缺。

（四）解法分析。

解法分析不僅要講清楚如何解題，更要展現為什么要這樣解題的思維過程，同時也要用多種途徑解決問題。

1。第一小題的解法：

（1）解法一：用平行線分線段成比例定理

思維分析過程有兩種：

①執果索因：

②由因導果：

（2）解法二：用相似三角形的判定和性質

將待證結論轉化為證明QC：CE=1：2，由題目的條件可知DE：DA=1：2，所以只要證QC：CE=DE：DA，那么就需要證明△QCE∽△EDA。

2。第二小題的解法：

（1）解法一：相似三角形面積比等于對應邊之比的平方，結合勾股定理。

思維過程是：面積問題相似三角形面積比

S+S=S？坩+=1？坩+=1？坩△CQE～△QEA～△EDA

（2）解法二：代數法。

設CQ=QF=a，那么CE=DE=2a，AD=4a，我們可以求得S=a，S=4a，S=5a，從而得到S+S=S。這里，用代數方法非常簡潔明了。

（3）解法三：面積的割大和補小。題目結論S+S=S中有“+”號，一般想到面積的割大補小。

①面積的割大：將△ADE沿著AE所在的直線對折，證明點D與點I重合，然后證明△QCE≌△QIE，從而得到S+S=S。

②面積的割小：將△QCE繞著點E順時針旋轉180度，易證點A、D、Q′共線。△QCE的面積轉化到△Q′DE，然后證明△Q′AE≌△QAE，從而得到S+S=S。

一題多解是對同一問題尋求不同的解決方法，多角度思考問題，培養學生的發散性思維和創造性思維。但是教師不能盲目追求解法多樣性，而是應該引導學生從解題思路差異性、解題過程簡潔性、解題思維優越性三方面進行比較，選出最優化的方法，力求簡單、直接。

（五）變式拓展。

數學本身也是主體建構的產物，她應該是活的，動態的，開放的，表現多維度的。一個問題的多種變化，其中既包括解題過程中的各種鋪墊，又包括對原問題的各種引申，如：改變條件，改變結論，一般化等。既然知識學習是一個建構的過程，那么就要突出學習者的主體作用，《數學課程標準解讀》要求我們關注學生的個體差異，讓不同層次的學生獲得不同的發展。

1。針對學困生的變式拓展，重在基本圖形的探究。以下三個變式，為學生能從復雜圖形中分解出基本圖形，并能分析其中基本元素及其關系積累活動經驗。

變式1。基本圖形：全等

已知：正方形ABCD中，DE=CF，求證：△ADE≌△DCF。

變式2。基本圖形：一線三直角

已知：Rt△ADE與Rt△ECQ，且AE⊥QE，求證：△ADE∽△ECQ。

變式3。基本圖形：一線三等角

已知：△ADE與△ECQ，且∠C=∠AEQ=∠D，求證：△ADE∽△ECQ。

針對學困生，我們要善于退，退到原始而不失重要性的地方，容易看清問題的本質。

2。針對中等生的變式拓展：將正方形變為菱形，其他條件不變。

變式4：如圖，E，F分別是菱形ABCD的邊DC，CB上的點，且DE=CF，以AE為邊作菱形AEHG，HE與BC交于點Q，連接DF。

（1）若E是CD的中點，求證：Q為CF的中點；

（2）連接AQ，設S=S，S=S，S=S，在（1）的條件下，判斷S+S=S是否成立？并說明理由.

思路分析：將△QCE的面積轉化到△Q′DE，然后證明△Q′AE的面積與△QAE的面積相等，從而得到S+S=S。

針對中等生，我們還可以將特殊問題拓展到任意情況。

變式5。如圖，E，F分別是正方形ABCD的邊DC，CB上的點，且DE=CF，以AE為邊作正方形AEHG，HE與BC交于點Q，連接AQ，設S=S，S=S，S=S。

（1）當CE=CD時，探究S，S，S的關系式，并說明理由。

（2）當CE=CD時，探究S，S，S的關系式，并說明理由。

（3）當CE=CD時，探究S，S，S的關系式，并說明理由。

思路分析：將中點變為三等分點，四等分點甚至N等分點，條件開放。E點位置改變，△QCE和△MDE不再全等，而是相似，面積的比值就是對應邊的平方比。我們仍然可以用幾何代數相結合的方法找出面積的數量關系。從特殊推廣到一般，得到四等分點和N等分點的時候的面積數量關系。

（1）當CE=CD時，延長QE交AD的延長線于點M，可證△CEQ∽△DEM，由相似三角形面積比是對應邊之比的平方，得到：S=4S，我們還可以得到△AEM的面積是△AEQ面積的兩倍，因此我們得出結論：2S=S+4S。

運用從特殊到一般的思想，我們不難得到：

（2）當CE=CD時，延長QE交AD的延長線于點M，同理：3S=S+9S。

（3）當CE=CD時，延長QE交AD的延長線于點M，同理：（n-1）S=S+（n-1）S。

3。針對學優生，我們可以將E點變為動點，變式拓展為動態幾何的問題。

變式6。正方形ABCD的邊長為1，E為線段CD上的動點，以AE為邊作正方形AEHG，HE與BC交于點Q。當點E從C向D運動時，求線段CQ的長度的最大值。

思路分析：在點E從C向D運動過程中，我們發現△CQE∽△DEA一直存在，用函數與方程的思想就能解決問題。設CE=x，DE=1-x，CQ=y，利用△QCE∽△EDA列出對應邊成比例的方程式，就能得到函數式：y=x-x=-（x-）+，最后用二次函數的圖像與性質求出最大值。

變式7。如圖，E，F分別是邊長為a的正方形ABCD的邊DC，CB上的點，且DE=CF，AE與DF交于點P，連接BP。當點E在直線CD上移動時，求BP的最小值。

思路分析：當E在直線CD上任意移動，保持DE=CF，那么運動過程中一直有△CDF≌△DAE，因此AE⊥DF恒成立。我們可以得到點P的運動軌跡是：在以AD為直徑的圓上運動（記線段AD的中點為圓心O）。所以，BP的最小值就是當BPO共線的時候最短，BP的最小值為。這里用的是轉化與化歸的思想。

（六）反思回顧。

數學思想方法是學生對數學的知識內容和所使用方法的本質認識。通過數學學習，使學生形成數形結合，轉化化歸，從特殊到一般，函數與方程等思想是數學課程的重要目的。

“圖形與證明”，對培養學生邏輯思維能力的作用顯而易見。如何引導學生探索圖形的性質，在數學活動中不斷發展合情推理，并體會到證明的必要性，理解證明的基本過程，掌握演繹推理的基本格式是初中“空間與圖形”學習的重點。學生通過靈活綜合應用知識，感悟數學思想方法，積累基本活動經驗，提高解決問題的能力。

五、說題的成效

杭州市及各區教師開展說題研究已經進行了多年，市、區多次進行了說題比賽和研討。經過這么多年的說題鍛煉，教師的學科專業素養得到了很快提升，學生分析問題、解決問題的能力也有了明顯提升。

（一）說題活動促進了教師迅速成長。

前陣子，筆者有幸擔任區中級評職模擬上課的評委，發現工作才六年的青年數學教師在分析例題環節比以前有了很大的進步。他們淋漓盡致地展示了例題解決的思維過程，而不是直接告訴學生如何解，而且他們對例題都及時進行了變式拓展，這讓在場的評委都很欣喜。近年來，說題活動通過層層選拔，次次觀摩，促進教師對教材、習題、試題、問題教學進行鉆研。只有教師對教材和練習了然于胸，注重問題解決思維過程，才能高屋建瓴，發展學生思維。說題有效促進了教師的專業化成長。

（二）說題活動提高了學生解決問題的能力。

平時上課，我班的學生在回答如何解決問題時，經常會出現這樣回答：

“我是從結論出發，一步一步倒推后找到這個思路的。”

“我是從這個已知條件入手，想到……”

“我是從另一個條件入手，找到了和他不同的解題方法……”

“老師，我發現這個題目可以把這個特殊條件：中點，去掉，換成一般條件：任意一點，結論仍然成立。”

……

也就是說，在教師的潛移默化下，學生學會了解決問題的思考方式。學生的數學學習活動不再是被動接受、記憶、模仿和練習。通過教師說題，學生也能學會說題，會用不同的途徑解決同一個問題，還會用同一個方法解決不同的問題。學生學習變得更主動積極，思維能力和創新意識得到了培養和發展。

六、說題的反思

（一）說題要避免模式化，應該突出個性。

說題有一般的模式，但是也不應太程式化，教師說題對題目的處理要有獨到之處，彰顯極富創意之處，只有這樣，才能給人耳目一新的感覺，煥發說題的活力。說題需要有“亮點”，不管哪種形式的說題，一定要力求重點突出，把體現本題個性特色的元素充分展示出來，這樣才能使聽者更好地了解說題的特點，才能發揮說題的特有功效。一個有特色的多媒體課件也可以讓說題更精彩。說題是說者和聽者的雙邊活動，無論在說題中采用哪種方法，都需要教師用豐富的情感激發聽者的興趣和熱情。

（二）說題的板書要簡練得當。

說題因時間有限，所以說題者不需把說的所有內容都板書在黑板上，只要把一些主要的解題環節板書在黑板上即可，使聽者能聽懂，但又不繁瑣。

（三）教師的解題能力有待提高。

中國古代文學家教育家劉勰說：“操千曲而后曉聲，觀千劍而后識器。”要有高質量的、精彩的說題，教師自身有較強的解題能力是關鍵，否則是無米之炊。所以，教師平時要多解題，多研究題，當然也要研究課標，研究中考的方向。

參考文獻：

[1]全日制義務教育數學課程標準解讀[M]。北京師范大學出版社，2002。

[2]變式教學研究[J]。數學教學，2003（01）。

[3]說課最需要什么[M]。南京大學出版社，2010。