數學建模背景下數據結構課程的討論與分析

黃玉蕾

摘 要：數據結構是計算機科學與技術專業一門重要的專業基礎課程。數據結構課程中各種算法思想包含了數學思維方法，通過學習數據結構，培養數學分析能力，同時參與數學建模過程，訓練數據結構算法的編程能力，二者相輔相成。本文以數學建模的中研究生錄取問題和跟導師之間的雙向選擇問題作為主要討論對象，將其轉化為0-1數據結構問題進行分析討論。

關鍵詞：數據結構； 數學建模； 課程改革； 教學方法

【分類號】G633.6

1 數學建模的特點

數學建模用數學語言描述實際現象的過程[1]。數學建模是聯系數學與實際問題的橋梁，尤其在工程界格外重視，成為科技工作者的必備重要能力之一。數學建模的教學本身是一個不斷探索、不斷創新、不斷完善和提高的過程。改變了過去以教師為中心、以課堂知識講授為主的傳統教學模式，數學建模課程創建了一個新的指導思想——以實驗室為基礎、以學生為中心、以問題為主線、以培養能力為目標來組織教學工作，通過教學使學生了解利用數學理論和方法分析和解決問題的全程，提高他們分析問題和解決問題的能力。使學生經常性的用數學去思考問題，利用計算機解決問題。

2 數據結構與數學建模

數學建模的基本思想方法是利用數學知識解決實際問題。而數據結構是計算機科學專業的重要的專業基礎課程，有大量抽象的數學概念和理論知識[2]。在教學過程中，將數據結構的算法融入到數學建模思想中，使學生將數學的理論和方法用計算機算法程序實現，這樣既可以將培養學生的編寫程序的能力又能夠提供數學的邏輯關系，增強了學生的動手能力，教學效果十分明顯。

3 數學建模下數據結構教學討論

本文根據研究生錄取問題和跟導師之間的雙向選擇問題作為主要討論對象，將此問題轉化為分別轉化成層次分析問題和線性規劃中的0-1 規劃問題[3]。

3.1 數學建模問題

首先建立研究生錄取遞階層分次結構模型，定義權重比例為0.6：0.4，對每個學生的綜合評價分數進行歸納，從15名候選同學中選出10位研究生。其次，用0-1 規劃模型進行學生和導師之間的雙向選擇。建立目標函數和約束條件，用lingo軟件求得：導師6分別和學生2、學生5以及學生6和學生12配對，導師3分別和學生3、學生9以及學生15配對，導師4分別和學生1、學生8配對，導師9和學生4配對。

用0-1 規劃模型[3]學生和導師之間的雙向選擇。

1、導師的學術水平評價：

導師的學術水平是四個方面體現的，分別為發表論文數、論文檢索數、編（譯）著作數、科研項目數。通過查閱資料得出對研究生導師的考核標準的分析，對于導師的學術水平的衡量，以上四個方面的重視程度是不同的，其中最看重的是論文檢索數、其次是科研項目數、對發表論文數和編（譯）著作數看的相對較低。故權值設定為：

對于導師的學術水平各項指標 ， ， ， ，是通過具體數目給出的，在此同時采用極差變換法，即由下面公式得到各導師的相應各指標量化值：

記導師學術水平向量為 ，采用下面公式得到對第 個導師的綜合水平的評價 ，即：

2、導師對學生的滿意度：

根據8個專家對每一個學生的評價，轉換為相應的數值4，3，2，1，然后用求算術平均的方法，得到每個學生的每項特長的綜合評分，用這個綜合評分與每位學生的五項特長的期望要求比較得出差異矩陣H，依據差異矩陣的數值 來劃分等級，具體做法為找出最大值和最小值確定長度區間，再除以欲劃分的等級數目，得到每個等級之間的等級長度：

用（很滿意，滿意，基本滿意，不滿意）來表示，由此得到每位導師對每位同學的各項特長的評價。

不滿意：數值介于區間：

基本滿意：數值介于區間：

滿意：數值介于區間：

很滿意：數值介于區間：

這四個等級就構成模糊集，取其對應的數值為1，2，3，4.

不考慮學生所報專業志愿前提下對學生的評價，考慮到導師選擇學生還是要看學生的志愿。所以得出專業、導師和學生之間的可分配關系如圖1所示。

3、學生對導師的滿意度

學生對導師的選擇，主要是根據學生自己的專業發展意愿，導師的基本情況和導師對學生的期望要求。集中體現在專業志愿和導師的學術水平上，導師的學術水平是客觀存在的，可以用導師的學術水平評價 來衡量，不同的學生對導師的滿意程度可以人為是取決于導師所從事的研究方向。類似的，可以通過加權方法來處理，即當導師研究方向與自己的第一志愿相同時，賦權值為1；當導師研究方向與自己的第二志愿相同是，賦權值為0.6；當導師研究方向與自己的志愿全不相同是，賦權值為0，其計算公式為：

其中志愿權值 取法同上，這時得到第 個學生對第 個導師的滿意度

4、雙方滿意度的綜合評價

確定了被錄取的學生和導師雙方對彼此的滿意度，我們認為學生和導師彼此的滿意度的和最大，兩者的差越少，兩者的相互選中的可能性越大，又有滿意度均為正，所以這里采用幾何平均的方法來綜合兩者的滿意度，定義導師和學生兩兩之間的相互滿意度為：

3.2 數據結構解決方法

在各個導師所帶學生數量沒有限制而學生只能選擇一個導師的情況下，為了達到一種選擇方案使得師生雙方的滿意度達到最大，我們可以把原問題轉化成0-1整數規劃問題，設決策變量為 （ 代表導師， 代表錄取學生）

目標函數：

約束條件：

其中：

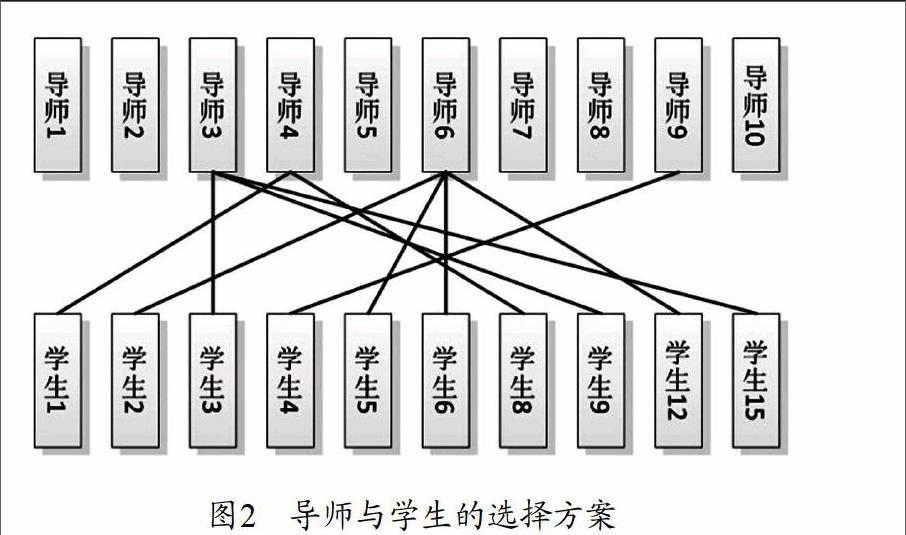
應用Lingo軟件對上面整數規劃問題求解得到目標值為7.047270，此時導師與學生的選擇方案為如圖2所示。

其中：導師6有四位學生，分別為學生2和學生5以及學生6和學生12，導師3有三位學生，分別為學生3和學生9以及學生15，導師4有兩位學生，分別是學生1和學生8，導師9有一位學生，為學生4。

3.3 0-1問題數據結構教學方法。

根據數據結構的特點，將0-1問題設置為以下講解方法。

1、實驗內容：

設有一個背包可以放入的物品的重量為S，現有N件物品，重量分別為W1，W2，W3……Wn。問能否從這n件物品中選擇若干件放入此包中，使得放入的物品的重量之和正好為S。

2、實驗的目的：

深入了解棧和隊列的特性，以便在實際問題背景下靈活應用，同時還將鞏固對這兩中結構的構造方法的掌握，接觸較復雜問題的遞歸算法的設計。

3、實驗設計思想：

（1）遞歸策略

在該問題中物品質量W[n]和包所能承受的最大重量maxweight都是又用戶自己任意定義的，在遞歸實現的過程中用到一個棧來實現。

（2）非遞歸策略

非遞歸策略思想的實現與遞歸策略類似，只是直接用定義一個棧來實現，同樣的物品質量W[n]和包所能承受的最大重量maxweight都是又用戶自己任意定義的。

4 總結

通過這道題，使我們鞏固了平時所學的知識，對數據結構中遞歸與非遞歸的思想有了進一步的理解和認識，更重要的是通過這個題目使我們更多的了解到數據結構在實際問題中的廣泛應用，同時在數據結構課程教學中融入數學建模思想方法，能夠很好地引導學生在學習的過程中善于發現問題、提出問題及解決問題，為后續課程打下堅實的基礎。

參考文獻

[1] 溫長剛，數學建模與“數據結構”課堂教學關系的探討與分析[J]電腦知識與技術 2014.8

[2] 景妮琴，淺談數學在數據結構教學中的應用[J]山西師范大學學報 2010.12

[3] 吳永輝，王建德，算法設計編程實驗[M]北京：機械工業出版社 2013.6