幾何畫板與中學數學教學的有效整合
張天群 齊改娣

【摘要】幾何畫板在數學教學中逐漸得到了較為深入的應用,本文中學數學教學的背景為基礎,以幾何畫板的幾個應用案例為切入點,分析了幾何畫板應用在中學數學教學中的應用和注意的問題反思.同時對幾何畫板在Word和PPT2010的插入方法.
【關鍵詞】幾何畫板;動態教學;整合
幾何畫板與數學教學的整合是指在教與學的過程中,充分而恰當的應用信息技術,使信息技術成為數學課程的有機組成部分,以便提高學生的信息技術能力和教師教與學的效率與質量,其理論基礎是學習理論、教學理論和信息傳播理論等,可以幫助教師教學,可以節約時間,有利于教師和學生的深層次溝通,可以幫助學生學習.有利于培養學生的直覺思維和形象思維.
幾何畫板是一款優秀的專業學科教學平臺軟件.能動態表現相關對象的關系,它使枯燥無味的課堂教學走向生動活潑的“動態教學”,真正向創新型教育教學發展.興趣是我們做任何事情的動力,也是學習最好的老師.成功的教學的關鍵是如何激發學生的興趣.孔子曰:“知之者不如好之者,好之者不如樂之者.”高中教學邏輯性與抽象性嚴密,學生普遍感到數學規律與邏輯的枯燥.幾何畫板的應用改變了數學教學的傳統模式,使數學課面目煥然一新.
一、幾何畫板的應用
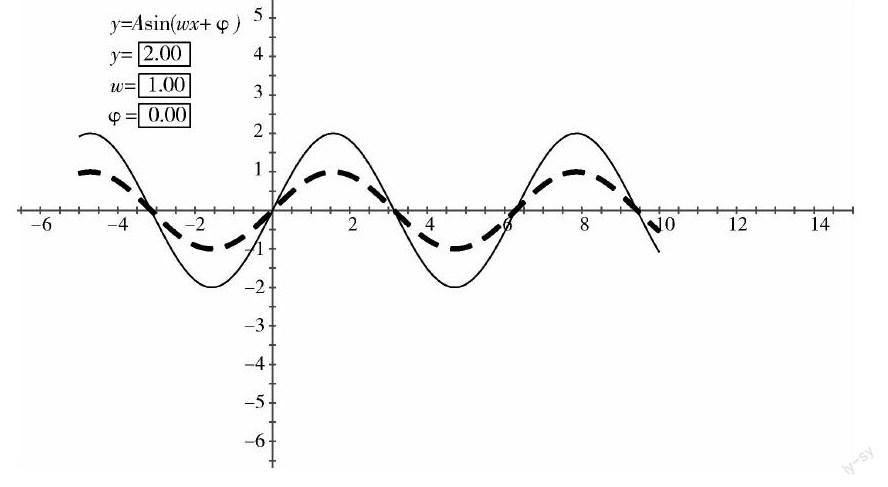
1.講授函數y=Asin(wx+φ)的圖像及性質這部分內容時,要探究 A, ω, 這 3 個量各自變化時,函數圖像會在正弦函數y=sinx的圖像的基礎上變換.而借助幾何畫板中改變 A 的值,就可以直觀地看出圖像在縱向上的拉伸或壓縮變化; ω 值的變化引起的是圖像在橫向上的拉伸或壓縮變化;改變 值后圖像會相應的左右平移.此時函數圖像隨著 A, ω, 的增大或縮小有著怎樣的變化就會非常直觀,這種不斷變化的波形曲線也會給學生留下深刻印象,從而激發起學生的學習興趣.
2.可以用幾何畫板根據函數的解析式快速作出函數的圖像,并可以在同一個坐標系中作出多個函數的圖像.如在同一個直角坐標系中作出函數y=x2 、y=x3 和 y=x12的圖像,比較各圖像的形狀和位置,歸納冪函數的性質.
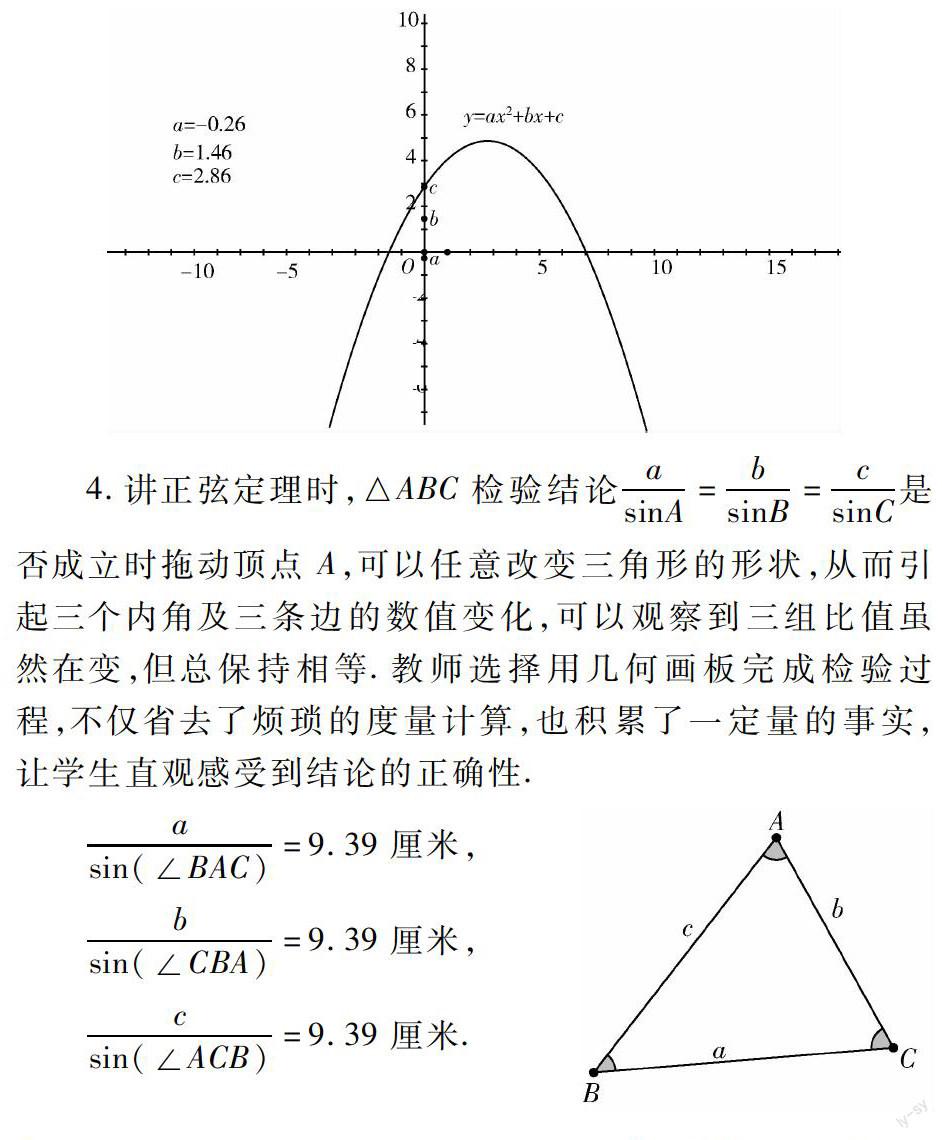
3.二次函數y=ax2+bx+c,從圖像中可以非常直觀地了解到隨著a、b、c三值的變化,函數圖像所產生的相應變化,通過這種方式,一方面讓學生對枯燥的數學知識重新產生了濃厚的興趣,另一方面也讓教學變得更加規范,幾何畫板下的二次函數圖像要比傳統的黑板上作畫精確許多.
4.講正弦定理時,△ABC檢驗結論asinA=bsinB=csinC是否成立時拖動頂點 A,可以任意改變三角形的形狀,從而引起三個內角及三條邊的數值變化,可以觀察到三組比值雖然在變,但總保持相等.教師選擇用幾何畫板完成檢驗過程,不僅省去了煩瑣的度量計算,也積累了一定量的事實,讓學生直觀感受到結論的正確性.
5.利用動態性和形象性,在老師的引導下,還可以給學生創造一個實際“操作”幾何圖形的環境.可以任意拖動圖形、觀察圖形、猜測并驗證,在觀察、探索、發現的過程中增加對各種圖形的感性認識,形成豐厚的幾何經驗背景,從而更有助于學生理解和證明.
在講橢圓的定義時,可以由“到兩定點 F1,F2的距離之和為定值的點的軌跡”入手.先讓學生猜測 P 點的軌跡是什么圖形,學生各抒己見之后,老師演示圖,學生豁然開朗:“原來是橢圓”.這時老師還可以改變PF1+PF2的值,使得 PF1+PF2=F1F2,滿足條件的點的軌跡變成了一條線段F1F2,甚至還可以得到PF1+PF2以上是教學中的典型實例,在這幾個例子中充分運用幾何畫板的動畫、移動、平移、旋轉、標識向量等高級功能,從中我們看到幾何畫板對中學數學教學是十分有利的.
二、幾何畫板與數學教學整合的思考
但也應注意:幾何畫板應用應該是以教學的需要為基準,只能作為輔助教學的工具與手段,在實際的教學過程中還需要教師詳細講解教學知識點以及經常與學生深入溝通交流,要充分地用它來引導學生的學習,讓它幫助學生思考,而不是代替學生思考和練習.
三、幾何畫板文件的在辦公軟件的插入
1.PPT 2010環境
方法一:點擊菜單欄最右邊的“加載項”可以看到“插入幾何畫板”命令,點擊后就可以選擇幾何畫板文件.
方法二:點擊“開發工具”里的“其他控件”按鈕,便可看到“1x幾何畫板控件”.(如果菜單里沒有顯示“開發工具”菜單.可以把“其他控件”加入到“快速訪問工具欄”,點擊左上角的下拉箭頭,選擇“其他命令”,在“從下列位置選擇命令”里選擇“開發工具選項卡”,找到“其他控件”,然后點擊“添加”,再點擊“確定”,這時左上角可以看到“其他控件”按鈕,左上角顯示“其他控件”按鈕)
2.Word 2010與方法二基本類似
總之,如果數學教師可以合理利用幾何畫板,則可以幫助學生逐漸養成自主學習的習慣,從而為其數學學習能力的提高奠定良好的基礎幾何畫板作為通用的數學教學手段,基于現代信息教學模式的發展,幾何畫板融入數學教學已經成為一個發展趨勢,提高的教學效果.只要我們發揮自己的創造性,潛心研究,就能不斷地加深對幾何畫板的理解和應用,不斷開發出適用于教學的優秀課件.
【參考文獻】
[1]孫云飛.淺談幾何畫板在函數教學中的應用[J].中國教育信息化,2012(8).
[2]胡廣斌.巧借幾何畫板提高學生學數學的興趣[J].改革與開放,2012(14).
[3]伍春蘭.基于“幾何畫板”的中學數學課堂“探究學習”的實踐與探索 [J].北京教育學院學報,2014,18(4):69-75.

