高職數學課程服務專業教學之研究

黃麗嫦（佛山職業技術學院，廣東 佛山 528000）

?

高職數學課程服務專業教學之研究

黃麗嫦
（佛山職業技術學院，廣東 佛山 528000）

摘要：隨著社會分工越來越精細，經濟發展對實用技術應用型人才的需求越來越大，高職教育應運而生。但高需求的同時也對高職教育提出了重視培養掌握應用技術的更高要求。高等數學作為基礎理論課，是其他專業課程學習的有力工具。但作為高職教育一部分的高等數學教學，目的在于為專業教學服務，與傳統高等教育相比有其特殊性。文章主要對為專業教學服務的高等數學高職教學的相關特點及改革展開討論研究。

關鍵詞：高等數學；高職教育；專業服務

由于高職教育的發展現狀以及社會對高職教育的要求，高職教育工作者必需從實際出發，并結合所教專業，遵循以應用為目的、夠用為度的原則來進行教學改革，體現聯系實際、注重應用，重視創新的高職教育特色。為此高職數學課程的教學，課程的目標不僅要求學生系統地掌握學科理論，更需要學生能夠靈活地運用相關知識解決相關領域的實際問題。結合專業特色，突出數學教育專業服務的應用性［1］，是高職數學教學的宗旨之一。

一、高職數學課程服務專業教學的現狀

（一）課程現狀分析

目前高職數學課程的教學，由于課程本身特點，往往從概念導出，公式運算法則推導進行介紹，內容比較抽象且枯燥，課程中的應用多會從理論角度出發，也限于數學角度的應用居多，另一方面，教材編寫不會顧及到各個專業，所心教材的例子難以與具體專業直接接軌。

（二）學情現狀分析

高職院校的招生對象來源于高中、中職學生，進入高職院校學習希望學習一定的技術來實現就業［2］，掌握專業能力是主要目標，他們普遍的數學基礎知識較差，對較為抽象的高等數學學習興趣不大，基礎知識、學習方法、學習環境、心理因素等造成他們學習效果不好，容易失去學習興趣，影響了數學教學效果。

（三）專業課程分析

高職院校不論是工科類或文科類的專業課，它們從學生入學開始，專業基礎課程和專業課都廣泛地使用高等數學的概念和運算，來進行專業課程中相關的分析和討論，使用到的數學概念和運算與數學課堂幾乎同步，此時如果數學課與專業課脫軌，學生的數學知識就難以應用于專業。

作者在多年的教學中，進行了數學課程服務專業教學探索研究，收到了成效，文章就數學課程教學服務電子類專業研究的一些策略和措施。

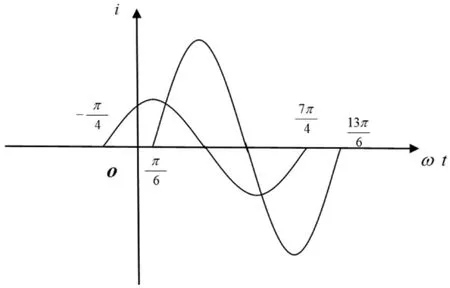
圖1

二、高職數學課程服務專業教學的改革和實踐

（一）了解專業需求

教師在制定《高等數學》課程的教學計劃時，先要了解授課班級相關專業課程，對數學概念和運算需求較大課程的教材先行學習，如《電工學》《電路數學》《信號與系統》等，同時也與專業老師溝通交流，關注專業課對數學內容及教學的要求，搜集學生在專業課堂中運用數學的情報，特別是學生運用數學知識最困難的地方，做到心中有數，再結合數學教材的教學內容制定教學計劃，在計劃制定時就要體現出服務專業的特點。

（二）內容選取和教學改革實踐

1.服務于專業課之數學概念教學

在函數概念的教學中，結合電子專業，選擇以下兩個電子學中常用的函數概念：

高等數學函數概念的教學，從服務于專業課的出發的初等函數概念，引入以下例子來進行教學和實踐：

例1：《電工學》中電流或電壓的正弦波形圖［3］

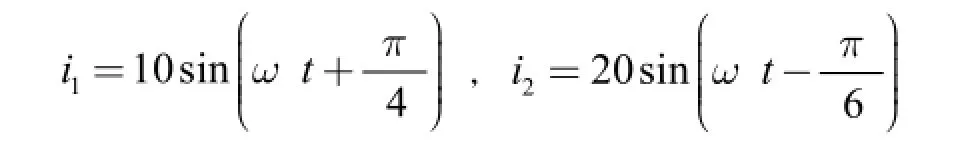
老師先從數學角度分析：正弦函數的特點：周期性、有界性，結合圖形分析并要求學生準確地描繪出圖象，并從中觀察其周期、最大值、起點等。

從專業課的角度分析：首先數學中的x、y軸也相應變成ωt、i軸，從圖中知道兩個電流的相位差為i1先到達最大值，i2后到達最大值，因此i1比i2的相位超前，幅值分別為10和20；所以在表達電學的電壓或電流的正弦波時，從數學中得出相應的最大值、起點在電學中解釋為幅值、初相，兩函數圖象的起點差即是兩電流間的相位差。

例2：指數信號［4］

指數信號的表達式為f（t）=Keat

式中a是實數，若a＞0，信號隨時間而增長，若a＜0，信號隨時間而衰減，在a=0的特殊情況下，信號不隨時間的變化而變化，

所以實際上，遇到較多的是信號衰減指數函數，其表達式為

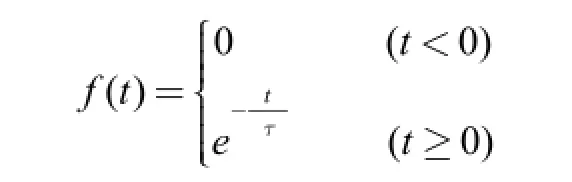
圖2

同時教師再提示：選擇指數函數信號，它還有一個重要的特性是它對時間的微積分仍然是指數形式，這是指數函數微積分運算的特點，這樣為以后利用微積分解釋和分析專業問題時提供方便。

以上兩個例子對電子專業的而言是常用的，故在講授函數的概念、圖象和性質時引入，通過數學及專業意義的互換，使數學更好地服務于專業，這樣學生對知識應用于專業課程就得心應手了，也增加了對函數的認識和興趣。

2.服務于專業課之數學運算教學

數學運算的結果如何服務于專業課，這是學生最為困難的地方，這要求教師精心去設計和指導，把數學運算是從數學定義和專業概念入手，所以在講授概念時注意講清數學概念的本質。如導數的概念的本質就是函數對自變量的瞬時變化率，在電子專業課中離不開變化率的話題：如速度、電流等，而定積分的概念的本質是無窮小的累加，如電容上電量的積累、電壓的平均值等，在教學中教師除了說清概念還要從運算的結果去引導學生解釋一些專業意義。

例3：如圖3所示，電容器在充電過程中兩極板的電壓u與時間t的關系為［5］

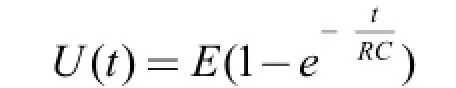
其中E、R、C為常數，求電容器的充電速度v；

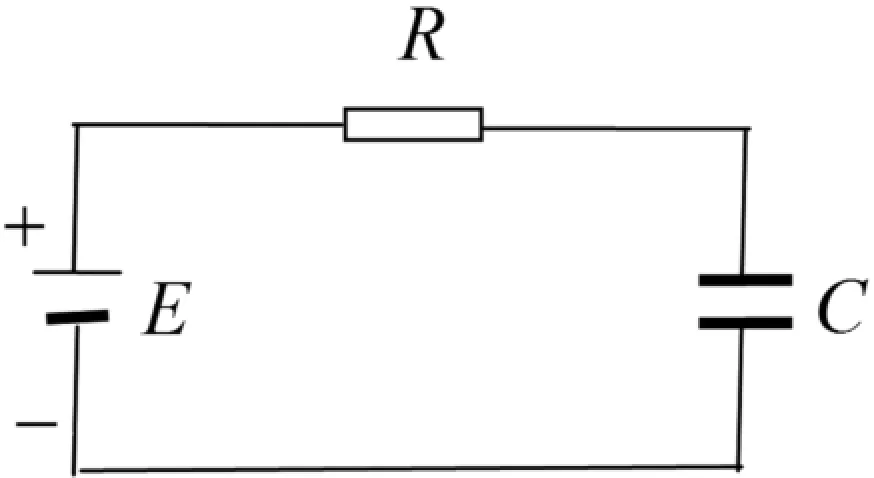
圖3

分析：充電速度為電壓U（t）對時間t的變化率，即求電壓U（t）的導數。

故

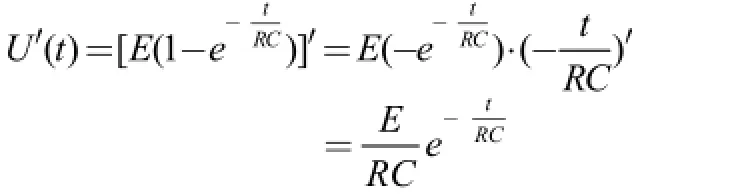
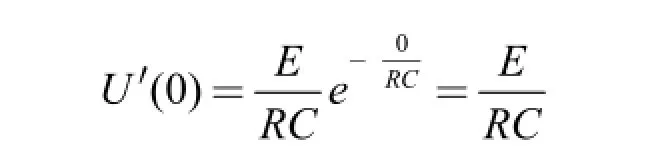
隨著電容兩端電壓的增高，充電速度漸慢，經過RC秒后，電容兩端電壓：

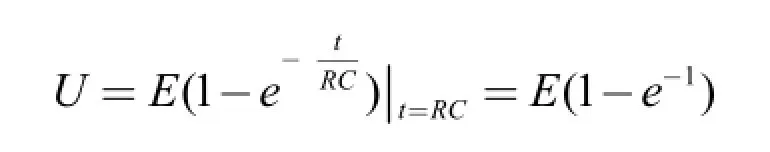
經過3秒后，電容兩端電壓：

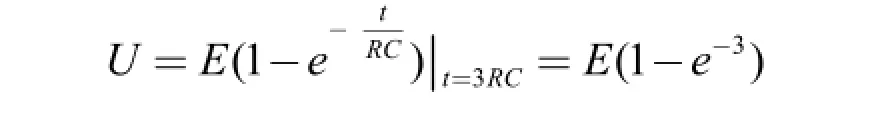
以后充電速度會越來越慢，一般認為經過3RC秒后充電停止，因為再往下后U的增加就更慢了。

例4：如圖4所示的電路中，當開關S合上后，其電流為［5］：

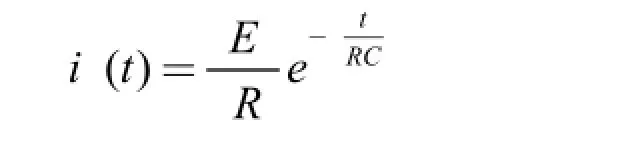
求其由t=0開始到 T時電容上的電壓。

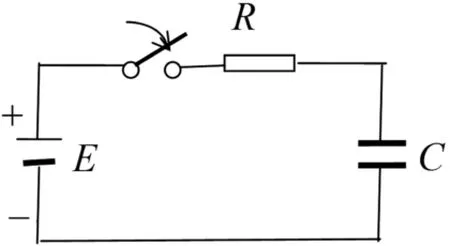
圖4

教師分析：求其由t=0開始到T時電容上的電壓，先從電學中有：

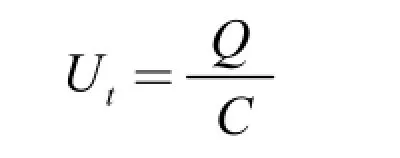
而求其由t=0開始到T時電量Q為電容上的電量積累，是變量無窮小的累加過程，在數學上這符合定積分概念的本質，有：

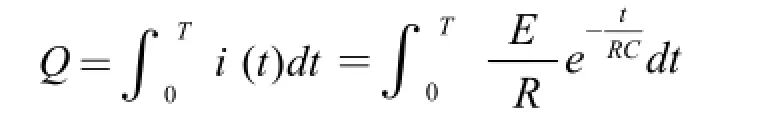
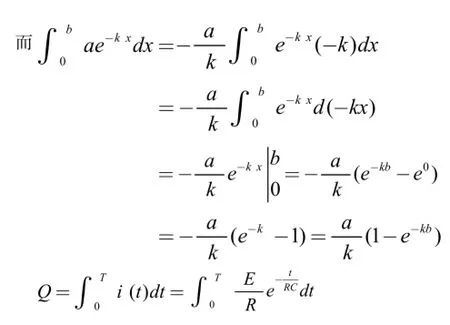
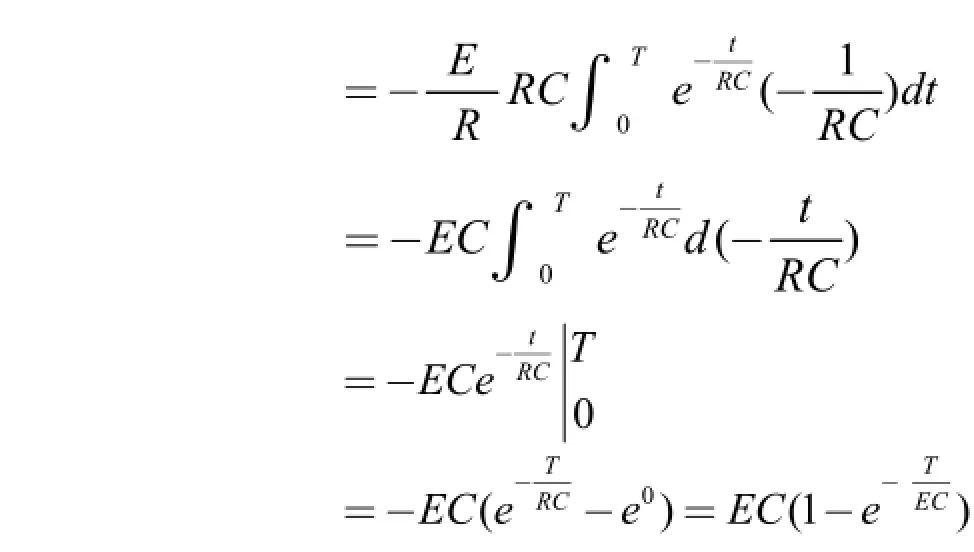
于是t=0開始到 T時電容器上的電壓為：

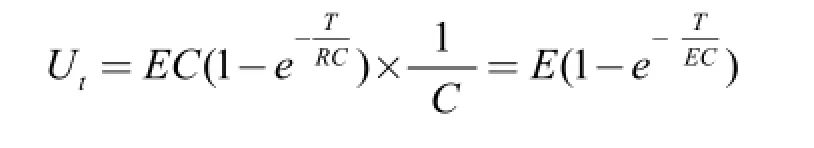
3.服務于專業課之建立數學模型的教學

單一的數學知識、單一的專業知識的課堂，數學教師和專業教師都會講授得精彩，但學生往往被動地去接受，在教學上中應加強這方面的教學改革，即如何讓學生去發現并應用，準確地在專業課堂應用數學的概念和運算，這需要教師花心思去實施，也即引導學生學會建立數學模型，如典型信號都是數學模型。

例5：建立單位斜變信號函數［6］

教師分析：在數學常用的五類基本初等函數中，最簡單的斜變函數是直線y=kx，單位斜升信號函數即選擇單調增加的k＞0時取k=1

因為從時間為零開始，建立的數學模型應選擇分段函數

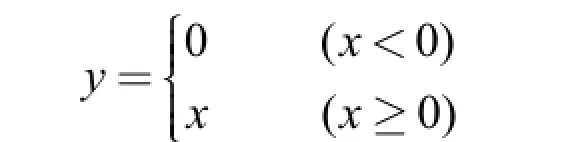
換成電學則得表達式為

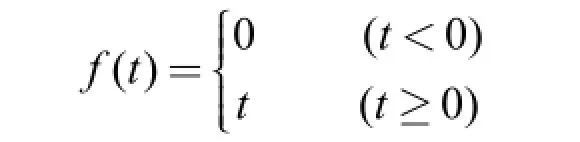
所以單位階躍信號函數就是選擇以上函數了。

三、教學改革的反思和改進

在工科各專業中，不同的專業使用數學知識點不盡相同，以上的論述只在電子專業班級上實施進行，并取得了一定的成效，但同一階段教師往往同時教授幾個不同專業的學生，難免在教學中要同時多方位去應對各個不同專業，這需教師同時在多個專業展開研究，逐漸形成更為成熟的改革方案，在高職數學課程服務專業教學改革上取得更大成效，惠及到各個專業的學生。

參考文獻

［1］王前鋒.淺談基于數學建模理念的高職數學教學改革探索［J］.教書育人，2015，10：106-107.

［2］曹峰.幸福教育：經濟發達地區職業教育的核心價值追求［J］.職業技術教育，2015，6：55-56.

［3］羅成林.電路數學［M］.人民郵電出版社，2005，9：6-6.

［4］鄭君里.信號與系統［M］.高等教育出版社，1981，5：7-7.

［5］羅成林.電路數學［M］.人民郵電出版社，2005，9：63-63.

［6］鄭君里.信號與系統［M］.高等教育出版社，1981，5：13-13.

中圖分類號：G642

文獻標志碼：A

文章編號：2096-000X（2016）13-0250-03

作者簡介：黃麗嫦（1962，06-），女，漢族，廣東中山人，本科，數學講師，佛山職業技術學院數理基礎教研室，研究方向：高職數學教學及計算數學。

Abstract：As the economical development recalls applied talents，higher vocational education emerges.Meanwhile，high requirements of the applied talents raise the point of teaching much more practical technologies compared with traditional higher education.Advanced mathematics is a basic theoretical course which serves as an important tool for learning professional courses.But the education of Advanced mathematics in higher vocational education is aiming at improving professional education，thus has its own specialties.This paper mainly discusses the related specialties and innovation in education of Advanced mathematics in higher vocational education.

Keywords：advanced mathematics；higher vocational education；serving professional education