層狀地基中自升式鉆井平臺插樁穿刺風險分析

林一，胡安康,，蔣瑋,，王藝陶

(1. 中集船舶海洋工程設計研究院，上海 201206； 2. 哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001)

?

層狀地基中自升式鉆井平臺插樁穿刺風險分析

林一1，胡安康1,2，蔣瑋1,2，王藝陶2

(1. 中集船舶海洋工程設計研究院，上海 201206； 2. 哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001)

摘要：自升式鉆井平臺進行海上插樁作業(yè)，遭遇上硬下軟的層狀地基時極易發(fā)生穿刺海損事故，從而造成嚴重的結構破壞和人員傷亡。這種層狀地基存在2種典型情況——硬粘土/軟粘土層、砂土/粘土層。本文考慮土層參數的影響，基于非線性數值方法對其地基承載力的變化規(guī)律進行了研究。以某400英尺工作水深的自升式鉆井平臺為例，采用Monte-Carlo法，考慮預壓載荷和土層參數的概率分布，對其在墨西哥灣某海域進行預壓載作業(yè)時發(fā)生穿刺海損的風險進行了分析，結果表明其風險值小于10%，為此類平臺進行相關作業(yè)的風險管理提供參考。

關鍵詞：自升式平臺；插樁穿刺；層狀地基；風險分析

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160422.1012.002.html

自升式鉆井平臺承擔著海洋油氣開發(fā)的重要任務，在各類海上可移動式鉆井平臺中占據主導地位。自升式鉆井平臺在海上就位進行作業(yè)時，首先需要通過加載使樁腿插入海底地基。當樁腿施加的壓載超過地基承載能力時，地基土發(fā)生沖剪破壞，樁腿得以繼續(xù)貫入直至地基承載能力等于壓載載荷，從而獲得平臺海上作業(yè)時的穩(wěn)定支撐，這一過程也稱為平臺的“預壓插樁”。

樁靴是自升式鉆井平臺進行預壓作業(yè)的主要受力結構，目前主要有2種形式[1]，底墊支撐式和獨立支撐式。獨立支撐式樁靴具有各樁腿相互獨立的特點，可以作業(yè)于略微傾斜或不平的海底，適用于更為廣泛的海底地質條件，目前應用于大部分新建自升式鉆井平臺上。

自升式鉆井平臺作業(yè)區(qū)域往往地質條件較為復雜，海底地基也常常呈現出層狀結構。獨立支撐式樁靴具有面積小、壓載大的特點[2]，當進行預壓插樁作業(yè)時樁靴遭遇上硬下軟的層狀地基，很可能發(fā)生穿透上覆硬土層進入下臥軟土層的情況，形成“穿刺”現象，輕者導致平臺急速傾斜、人員傷亡、設備受損，重者甚至會引起平臺的整體傾覆。HSE(健康、安全、環(huán)境國際會議)通過對自升式鉆井平臺歷年與基礎相關的事故進行統(tǒng)計發(fā)現[3]，穿刺破壞所占比重最高，約占事故總數的53%，且正以每年1～2起的速度增加，每次事故造成的經濟損失約為100萬～1000萬美金：2009年10月，在西非象牙海岸“Sapphire Driller”進行升船壓樁時艏部樁腿發(fā)生穿刺，多處節(jié)點發(fā)生沖剪破壞，平臺傾斜7.8°；2009年5月，“HYSY941”在中國南海海域進行探井作業(yè)時，艏部樁腿發(fā)生穿刺導致船艏傾斜6.2°，4根斜撐、2根內水平撐發(fā)生變形。由于海洋平臺穿刺事故的頻繁發(fā)生，目前對于穿刺破壞的原因和發(fā)生機理的研究已逐漸成為一個熱點問題。

對穿刺破壞現象進行研究，根本在于準確預報插樁過程中樁靴與海底地基的相互作用。目前對于圓形基礎在復雜地基條件下的承載力研究方法主要有2種：以試驗為基礎的傳統(tǒng)分析法[4]和有限元數值分析法[5]。傳統(tǒng)分析法中具有代表性的研究成果是1969年Brown&Meyerhof[6]根據圓形樁靴模型試驗歸納出的著名的Brown和Meyerhof公式；Skempton在其基礎上進行了深度系數修正[7]，目前被廣泛應用于樁靴貫入深度和穿刺可能性評估。近十幾年來，有限元數值分析法得到了飛速發(fā)展：L.Kellezi、G.Kudsk[8-10]等采用有限元技術分析了自升式平臺在北海風暴自存工況時樁靴與巖土之間的相互作用；中國石油大學的戴兵[11]基于數值方法對自升式平臺樁靴在層狀土中的承載能力進行了研究。

本文首先研究了非線性數值方法中的關鍵技術，然后就土層參數對容易發(fā)生穿刺事故的典型地質情況—硬粘土/軟粘土層、砂土/軟粘土層的影響進行了討論。在此基礎上，以某400英尺工作水深的自升式鉆井平臺為例，采用Monte-Carlo法，考慮預壓載荷和土層參數的概率分布，對其在墨西哥灣某海域進行預壓載作業(yè)時發(fā)生穿刺海損的風險進行了分析，給出了解決此類工程問題的數值解決方案。

1數值仿真關鍵技術

1.1基本方程

平臺預壓插樁過程中，土體在承受插樁載荷時會發(fā)生擠壓和剪切破壞，產生非線性變形，通常采用塑性增量理論來描述，即將載荷離散成若干增量段，針對每一級載荷增量將彈塑性方程線性化。

假設土體體積為V，作用在土體上的表面載荷為Ti，體積力為Fi，當載荷有一增量后，土體的應變εη，應力ση，位移uj及其增量需要滿足力學平衡定律、應力應變關系、幾何關系和邊界約束。

(1)

(2)

(3)

(4)

式中：ΔFi為表面載荷增量，Δση為應力增量，Δεη為應變增量，Δuj為位移增量，ΔTi為體積力增量。

1.2材料模型

土體受載的應力途徑、時間歷程和固結壓力等均對其變形有較大的影響，因此選擇合適的土體材料模型對計算其承載力至關重要。本文選用在海洋工程領域廣泛應用的Mohr-Coulomb(簡稱M-C)模型，該模型的破壞面與中面主應力無關，能反映巖土材料抗壓強度不同的特性對正應力的敏感性。

M-C模型認為當土體內任一平面上的剪應力達到或超過土的抗剪強度時，將發(fā)生剪切破壞。其屈服準則(見式5)包括粘聚力的各向同性的硬化和軟化，且勢函數完全光滑，確保了塑性流動方向的唯一性。

(5)

式中:c為粘聚力，N；σn為受力面上的正應力，Pa；φ為內摩擦角，°。

此外，由于樁靴/土體在相互作用時，土顆粒與結構物的相互位置不斷發(fā)生改變。為了體現這種復雜的接觸現象，本文采用主從面接觸算法來解決這一問題，而插樁過程中樁靴和土體之間的摩擦作用采用經典的庫侖摩擦來考慮。

1.3加載點位置

對平臺插樁作業(yè)進行數值分析時，通常在樁靴合適的位置選取一加載點，樁靴的運動與加載點相關聯(lián)，加載點的位置將直接影響到地基土的破壞模式和承載力。

值得注意的是，加載點不在重心處時，會導致樁靴結構繞其重心發(fā)生轉動，這與工程實際是不相符的。本文加載點位置的選擇見圖1，距樁靴頂部以0.1 L遞增。圖2顯示，最佳加載點位于樁靴結構的重心位置處(l=0.6 L)，此時樁靴結構發(fā)生平動，且承載力最大，這也與文獻[12]的研究結果相一致。加載點位置的不同對樁靴承載力影響在3%以內。

圖1　加載點示意圖Fig.1　Loading points

圖2　加載點對承載力的影響Fig.2　Effect of loading point on bearing capacity

1.4網格劃分

平臺插樁作業(yè)過程中樁土的相互作用是一個高度非線性過程，因此數值分析時網格劃分的合理性與計算精度和效率密切相關：樁靴周圍的網格尺寸必須足夠細密，插樁區(qū)域以外的土體不與樁靴產生接觸變形，只進行應力的傳遞，網格尺寸可以適當加粗。

本文選擇了3種網格劃分方案進行對比分析，分別對應樁靴接觸區(qū)域的網格尺寸為0.8 m×0.8 m、1.2 m×1.2 m和1.6 m×1.6 m。圖3結果所示，3種方案計算結果存在6%左右的差異，粗網格得到了較高的承載力結果，這是由于尺寸較大的單元低估了高應力點的應力和應變值，導致土體的大變形現象不能及時發(fā)生造成的。數值計算中計算時間通常由最小網格尺寸決定，在48 G內存的服務器上方案1～3的計算時間分別為2、1和0.25 h，綜合考慮計算精度和效率，本文采用方案2的網格劃分方案進行計算。

1.5 地基邊界

實際工程中，與樁靴相互作用的海底地基具有無限邊界，但在數值分析中通常截取有限的邊界進行位移約束，并假定邊界以外的土體不受影響。地基邊界的選取通常較難確定，較小的地基邊界會導致計算精度無法滿足工程應用的要求，較大的地基邊界則會導致計算時間的增加。文獻[13]提出地基土徑向取12B(B為樁靴直徑)，深度取10B，以保證地基邊界在塑性變形區(qū)域之外，其他文獻對地基邊界的取值也大致如此。

本文選取了3個計算方案進行對比計算，其徑向和深度方向的長度分別對應為12B×10B、6B×5B和4B×4B。圖4結果所示。

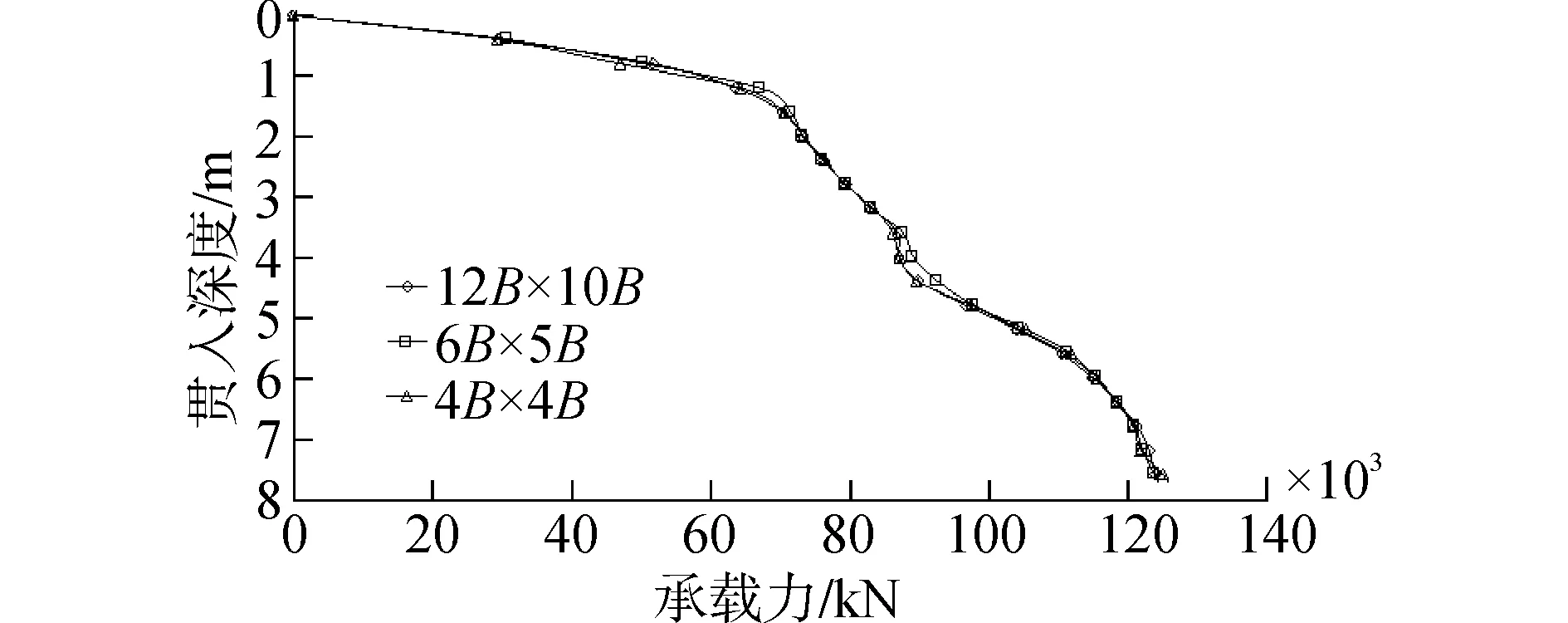
圖4　地基邊界的影響Fig.4　Effect of foundation boundary

3種計算方案的誤差小于1%。這是由于在本例中，3種方案的地基邊界均落在平臺插樁引起的土體塑性區(qū)域之外導致的。在48 G內存的服務器上方案1～3的計算時間分別為4、1和0.5 h，綜合考慮計算精度和效率，本文選取方案2的地基邊界進行計算。

1.6 校準性研究

為了對本文使用的數值計算方法的可靠性進行研究，對土層特性為上層粘土不排水抗剪強度Sut=120 kPa、下層粘土不排水抗剪強度Sub=24 kPa的成層土進行比較分析。表1結果顯示，對于成層土，有限元數值分析法與傳統(tǒng)分析法計算結果存在一定差異，約在10%左右。究其原因，對于復雜地基情況，傳統(tǒng)分析法存在大量假設，具有一定的局限性，而有限元數值分析法在數值模擬的關鍵參數選取上也有待進一步研究。

表1 　成層土承載力對比

2層狀地基承載力分析

海底地基土大多呈現為層狀結構，當出現上硬下軟的土層情況時，容易引起平臺插樁作業(yè)時樁靴發(fā)生突然下沉貫入的穿刺現象，對結構安全性造成危害。容易誘發(fā)插樁穿刺的典型土層情況有2種：上層為硬粘土，下層為軟粘土；上層為砂土，下層為粘土。層狀地基承載力研究是其穿刺破壞機理分析的基礎，因此本文采取非線性有限元方法，試圖探索土層參數對上硬下軟層狀地基承載力的影響。

2.1數值模型

數值模型的合理建立是層狀地基承載力準確預報的基礎。參照上文數值仿真關鍵技術的研究成果，采用ABAQUS軟件建立了樁靴/地基的有限元數值模型(圖5～6)。

圖5　樁靴模型Fig.5　Spudcan model

在平臺插樁貫入過程分析中，主要考慮貫入深度和地基承載力之間的關系，并不關注樁靴的結構變形，因此將其假定為剛體。加載點位置在樁靴結構重心處，加載方式為施加強迫位移。

層狀地基的邊界條件設定為側面施加水平方向約束，底面施加固定約束，頂面自由，網格劃分和地基邊界按上文討論的結果進行選取。土體材料模型選用M-C模型，采用庫侖摩擦模擬樁靴切向運動的影響，摩擦系數根據文獻[14]取為0.6。

圖6　樁土模型Fig.6　Pile-soil model

2.2 硬粘土/軟粘土層

對于硬粘土/軟粘土層的地基承載力，工程上通常采用Brown&Meyerhof方法和投影面積法來計算。自升式鉆井平臺插樁作業(yè)時，海底地基粘土層的破壞模式為樁靴周圍的沖剪破壞，樁靴在貫入過程中地基承載力達到峰值后會突然降低，是否會發(fā)生穿刺現象取決于一些土層參數，本節(jié)采用非線性有限元方法，根據表2中的計算方案進行分析。

表2　硬粘土/軟粘土層計算方案

1)上下土層強度比

上下土層強度比Sut/Sub是考察層狀地基承載力的重要指標(如圖7所示)。

圖7　上下土層強度比對承載力的影響Fig.7　Effect of strength ratio of upper and lower soil layer

考察硬粘土層的不排水抗剪強度Sut為80 kPa和120 kPa兩種情況，上下土層強度比Sut/Sub在1.2～6變化，硬粘土層的厚度為1倍基礎直徑，上下土層的自重均為18 kN/m3，計算工況為工況1～7。

硬粘土層不排水抗剪強度Sut為120 kPa時，地基承載力隨著貫入深度的增加而提高，到達峰值后呈大幅下滑趨勢，最后趨于一個穩(wěn)定的值。圖7計算結果顯示，地基土的最終承載力取決于下層軟粘土層的強度，隨其增加而增大。

對于插樁穿刺問題，關注的重點是地基土承載力的峰值及此時的插樁深度，隨著上下土層強度比的減小，地基承載力的峰值也隨之增加，承載力曲線的拐點位置，即可能的穿刺深度隨之增加，因而發(fā)生穿刺的風險也隨之減小。

為考察硬粘土層不排水抗剪強度變化的影響，在上下土層強度比一致的前提下，對Sut為80 kPa的情況分析后發(fā)現，上層土不排水抗剪強度的減小會降低地基承載力的峰值，在相同的土層強度比的情況下，會導致平臺插樁穿刺風險的增加。

2)上層土相對厚度

上層土相對厚度H/D同樣是影響層狀地基承載力的重要因素。假定上下土層強度取為定值2.5，硬粘土層不排水抗剪強度為80 kPa，相對厚度H/D在0.5～1.2變化，上下土層的自重均為18 kN/m3，計算工況為工況8～12。

圖8計算結果表明，各種工況下均存在插樁穿刺的可能性，隨著上層土相對厚度的增加，地基承載力及其峰值均逐漸提高，出現峰值的曲線拐點，即穿刺可能發(fā)生的位置也相應增加，但均未到達上下土層的分界線，說明軟土層從樁靴貫入海底地基開始就產生影響。各工況下承載力曲線最后趨于一致，說明地基土最終承載力僅取決于下層軟粘土的強度。值得注意的是，上層土相對厚度的增加會導致承載力曲線隨貫入深度下降更快，因此發(fā)生插樁穿刺的可能性也更大。

圖8　上層土相對厚度對承載力的影響Fig.8　Effect of relative thickness for upper clay

3)標準化抗剪強度

標準化抗剪強度Sub/γD是表征下層粘土對層狀地基承載力影響的無量綱物理量。假定上下土層強度比一致，比值均為1.5，上下土層的自重均為18 kN/m3，下層土不排水抗剪強度分別為Sub為30、40、60 kPa，對應的標準化抗剪強度分別為Sub/γD 為0.083、0.111、0.167，計算工況為工況13～15。

圖9計算結果顯示，在上下土層強度比和上層土相對厚度一致的情況下，地基最終承載力取決于下層軟粘土不排水抗剪強度，隨標準化抗剪強度增加而提高。此外，標準化抗剪強度的增加導致承載力曲線隨貫入深度下降得更為平穩(wěn)，即發(fā)生插樁穿刺的可能性更小，這與Young在樁靴貫入實驗中得到的研究結論相一致[15]。

圖9　標準化抗剪強度對承載力的影響Fig.9　Effect of normalized shear strength

4)土體強度非均勻系數

土體強度非均勻系數kD/Sub是表征下層粘土強度變化的無量綱物理量。前文假定下層軟粘土層不排水抗剪強度不隨土層深度而變化，即土體不均勻系數k=0，但飽和海底地基中土體不排水抗剪強度通常隨深度線性增加，即k>0。因而假定上下土層強度比一致，比值均為2，上下土層的自重均為18 kN/m3，下層軟粘土的強度變化梯度k分別為0、1、2、3 kPa/m，對應的土體強度非均勻系數分別為kD/Sub為0、0.5、1.0、1.5，計算工況為工況16～19。

圖10計算結果顯示，在上下土層強度比和上層土相對厚度一致的情況下，隨著土體強度非均勻系數的增加，軟粘土層的平均強度將接近于上層土，從而減弱軟粘土層的軟化效應，導致地基承載力曲線的峰值也隨之提高，同時最終承載力也相應提高。

圖10　土體強度非均勻系數對承載力的影響Fig.10　Effect of non-homogeneity factor

2.3砂土/粘土層

對于砂土/粘土層的地基承載力，工程上通常采用Hanna&Meyerhof方法和投影面積法來計算。本節(jié)采用非線性有限元方法，根據表3中的計算方案分析土層參數對承載力的影響。

表3　砂土/粘土層計算方案

1)粘土不排水抗剪強度

砂土/粘土層狀地基中，通常砂土層的強度要遠大于粘土層，但粘土層對于地基承載力的弱化效應不可忽略，因此粘土不排水抗剪強度的影響需要引起關注。假定砂土層的摩擦角φ為38°，厚度為0.5倍基礎直徑，粘土層的自重為18 kN/m3，不排水抗剪強度分別為20、40、80、120 kPa，計算工況為工況20～23。

圖11計算結果表明，粘土不排水抗剪強度對地基承載力存在顯著影響，地基承載力隨軟粘土不排水抗剪強度的增加而增大，到達峰值后快速下降，發(fā)生插樁穿刺的風險增加。值得注意的是，承載力曲線峰值出現的位置均未到達土層分界線，這也說明軟粘土層的弱化效應明顯，而當下層粘土不排水抗剪強度較大，如120 kPa時，承載力曲線到達峰值下降，越過土層分界后又呈逐漸上升的趨勢，這也是與上硬下軟粘土層情況存在明顯不同的地方。

2)砂土摩擦角

砂土摩擦角的大小通常將直接影響砂土層的強度。假定下層粘土的不排水抗剪強度為40 kPa，自重為18 kN/m3，砂土層的厚度為0.5倍基礎直徑，摩擦角φ為28°、30°、32°、34°、36°、38°，計算工況為工況21、工況24～28。

圖12計算結果顯示，在下層粘土強度保持一致的情況下，地基承載力隨砂土摩擦角的增加而緩慢提高，當承載力曲線達到峰值后，下降的速度隨砂土摩擦角的增加而減緩，發(fā)生穿刺的風險隨之變小。此外，與粘土層強度的影響類似，承載力曲線很快就到達峰值然后減小，說明砂土/粘土層發(fā)生穿刺的位置要小于上硬下軟粘土層情況，這在工程中是值得注意的。

圖11　粘土不排水抗剪強度對承載力的影響Fig.11　Effect of undrained shear strength for clay

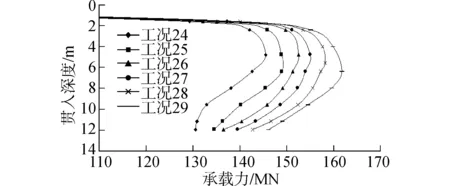
圖12　砂土摩擦角對承載力的影響Fig.12　Effect of sand friction angle

3)砂土層相對厚度

砂土層相對厚度同樣是影響砂土層承載力曲線的重要指標。假定下層粘土的不排水抗剪強度為40 kPa，自重為18 kN/m3，砂土層的摩擦角φ為38°，其相對厚度H/D分別為0.5、0.75、1.0，計算工況為工況21、工況29～30。

圖13計算結果顯示，在砂土層和粘土層強度保持一致的情況下，地基承載力隨砂土層相對厚度H/D的增加而增大，承載力曲線達到峰值后，下降的速度隨砂土層相對厚度的增加而增大，發(fā)生穿刺的風險隨之增加，需要在工程應用時關注這一現象。

3插樁穿刺風險分析

在對層狀地基承載力分析的基礎上，以一121.92 m水深自升式鉆井平臺為例，結合土層參數的概率模型，對其在墨西哥灣某海域預壓插樁過程進行數值分析，并采用Monte-Carlo方法對發(fā)生穿刺海損的風險進行評估。

3.1平臺/地基信息

以中集船舶海洋工程設計院(ORIC)自主研發(fā)的CIMC400自升式鉆井平臺為例，對其預壓插樁工況下發(fā)生穿刺海損的可能性進行評估。該平臺三個樁腿呈菱形連接，具備獨立樁靴，最大工作水深121.92 m，最大鉆井深度9 144 m ，入級ABS船級社(圖14)。

圖13　砂土層相對厚度對承載力的影響Fig.13　Effect of relative thickness for clay layer

圖14　CIMC400自升式鉆井平臺示意圖Fig.14　Profile of CIMC400 Jack-up drilling unit

目標平臺的作業(yè)地點選定為美國墨西哥灣某海域，以泥沙質海底為主，風、浪、流等海洋環(huán)境條件較好，適合進行鉆井作業(yè)。預壓作業(yè)前進行了井場工程地質調查，得到的相關地層資料見表4，第1層為淤泥質粘土，第2層為粉質粘土，第3層為砂土，第4層為粘土，屬于典型的砂土/粘土層狀地基，應考慮發(fā)生穿刺的可能性。

表4　井場地層資料

3.2地基承載力計算

對平臺插樁穿刺問題進行分析時，考慮到諸多不確定性因素的存在，通常以一個合適的穿刺安全系數Fs，即層狀地基極限承載力與樁腿最大預壓載荷的比值，來表征發(fā)生穿刺的可能性。理論上，Fs>1.0即可進行插樁作業(yè)，而為了保守起見，工程應用時通常認為穿刺安全系數Fs>1.5時，該井位作業(yè)時不會發(fā)生穿刺現象。

對于本文的海底地基情況同樣采用有限元方法進行分析：承載力曲線先隨樁靴貫入深度逐漸增加，進入砂土層后曲線很快到達峰值，隨后受到軟弱下臥層的影響而迅速減小，進入粘土層后，由于下層為砂土層，因此承載力曲線逐漸回升。目標平臺的預壓載荷為180 000 kN，其最終插樁深度為14.16 m，承載力曲線峰值為194 918 kN，位于19.96 m處(圖15)。據此判定Fs= 1.083，具有較大的穿刺風險，需考慮土層參數的不確定性進一步進行風險分析。

圖15　預壓載—貫入深度曲線Fig.15　Pre-load and penetration depth curve

3.3土層參數概率模型

土層參數存在離散性，表3給出的土層參數僅僅反映了所測參數的平均值，而土質取樣、測試方法的不同都會導致其不確定性的產生，目前在土層參數的不確定性研究方面已有了不少成果，本文參照美國石油協(xié)會規(guī)范API RP-2A-LRFD給出了這些土層參數的均值系數、變異系數和概率模型(表5)，作為后續(xù)風險分析的基礎。

表5　土層相關參數統(tǒng)計分布

3.4風險分析

通常認為，預壓載荷是自升式鉆井平臺服役期間內地基土可能承受的最大垂向載荷，因此可以確定平臺預壓插樁作業(yè)的極限狀態(tài)方程：

(6)

式中:FC為地基極限承載力，N；FP為預壓載荷，N。

土層參數的不確定性導致地基極限承載力FC存在隨機特性，在對1×106個數據樣本統(tǒng)計后采用柯爾莫哥洛夫K-S檢驗法進行擬合檢驗，以得到其概率統(tǒng)計分布。擬合結果表明(表6)，地基極限承載力FC和預壓載荷FP的概率模型均符合對數正態(tài)分布。

表6地基極限承載力及預壓載荷的統(tǒng)計分布

Table 6Statistical distribution of foundation ultimate bearing capacity and pre-load

參數概率模型均值系數變異系數地基極限承載力對數正態(tài)1.0850.006預壓載荷對數正態(tài)1.00.14

基于式(6)給出的極限狀態(tài)方程，根據表5中地基極限承載力以及預壓載荷的統(tǒng)計分布，通過Monte-Carlo法對平臺插樁穿刺可能性進行計算。計算結果表明，若考慮預壓載荷的隨機性，發(fā)生插樁穿刺的可能性為9.916%，若不考慮其隨機性，發(fā)生插樁穿刺的可能性為9.702%，預壓載荷的隨機性影響極為有限。因而建議在工程應用中，可以不考慮預壓載荷的隨機性以提高計算效率。

4結論

本文以CIMC400自升式鉆井平臺為例，考慮土層的參數影響，在對海底層狀地基承載力進行研究的基礎上，采用非線性有限元方法對平臺作業(yè)時發(fā)生插樁穿刺的風險進行了分析，得到結論如下：

1)自升式鉆井平臺插樁入泥過程是一個高度非線性過程，目前對于層狀地基承載力計算在理論上尚不明確，對于復雜地基情況具有一定的局限性，而非線性有數值模擬技術在處理此類問題上具有一定的優(yōu)勢，且能夠滿足工程應用的要求。

2)土層參數對層狀地基承載力存在影響：上下土層強度比、上層土相對厚度、標準化抗剪強度對硬粘土/軟粘土層的影響明顯，粘土不排水抗剪強度、砂土摩擦角、砂土層相對厚度對砂土/粘土層的影響較大。

3)在本文給定的作業(yè)海域和地層資料下，考慮土層參數的隨機分布，目標平臺存在一定的插樁穿刺風險，采用Monte-Carlo法計算發(fā)現，在工程分析時可以不考慮預壓載荷的隨機性。

參考文獻：

[1]陳宏. 桁架腿自升式平臺極限刺穿深度的計算[J]. 中國海洋平臺, 2011, 26(1): 44-51.

CHEN Hong. Calculation of the punch through capacity of jack-up with truss-type legs[J]. China offshore platform, 2011, 26(1): 44-51.

[2]張異彪, 楊文達. 層狀地層中自升式鉆井平臺樁腳穩(wěn)定性分析[J]. 海洋石油, 2005, 25(4): 91-95.

ZHANG Yibiao, YANG Wenda. Footing stability of jack-up rig in the layered soil[J]. Offshore oil, 2005, 25(4): 91-95.

[3]DIER A, CARROLL B. Guidelines for jack-up rigs with particular reference to foundation integrity[R]. Norway: Health & Safety Executive, 2004.

[4]BURD H J, FRYDMAN S. Bearing capacity of plain strain footings on layered soils[J]. Canadian geotechnical journal, 1997, 34(2): 241-253.

[5]LOVE J P, BURD H J, MILLIGAN G W E, et al. Analytical and model studies of reinforcement of a layer of granular fill on a soft clay subgrade[J]. Canadian geotechnical journal, 1987, 24(6): 611-622.

[6]BROWN J D, MEYERHOF G G. Experimental study of bearing capacity in layered clays[C]//Proceeding of the 7th International Conference on Soil Mechanics And Foundation Engineering. Mexico City, 1969, 2: 45-51.

[7]SKEMPTON A W. The bearing capacity of clays[C]//Proceedings of the Building Research Congress. London, 1951, 1: 180-189.

[8]KELLEZI L, DENVER H, KUDSK G, et al. FE skirted footings analyses for combined loading and layered soil profile[C]//Proceedings of the 14th European Conference on Soil Mechanics and Geotechnical Engineering. Madrid, 2007: 9-14.

[9]KELLEZI L, KUDSK G, HOFSTEDE H. Skirted footings capacity for combined loads and layered soil conditions[C]//International Conference on Foundations (ICOF). Dundee, Scotland, 2008: 24-27.

[10]KELLEZI L, KUDSK G, HOFSTEDE H. Jack-up rig foundation design applying 3D FE structure-soil-interaction modeling[C]//International Conference on Foundations (ICOF). Dundee, Scotland, 2008: 28-33.

[11]DAI Bing, DUAN Menglan, WANG Fei, et al. Proactive prediction methods of punch-through analysis on jack-up rigs[C]//Proceedings of the 20th International Offshore and Polar Engineering Conference. Beijing, 2010.

[12]舒恒. 離岸工程地基基礎承載力研究[D]. 杭州: 浙江大學, 2009: 10-100.

SHU Heng. Bearing capacity of offshore foundation[D]. Hangzhou: Zhejiang University, 2009: 10-100.

[13]HOSSAIN M S, RANDOLPH M F. Investigating potential for punch-though for spud foundations on layered clays[C]//Proceedings of the 17th International Offshore and Polar Engineering Conference, ISOPE. Lisbon, 2007: 1510-1517.

[14]KELLEZI L, STROMANN H. FEM analysis of jack-up spudcan penetration for multi-layered critical soil conditions[C]//Spudcan Penetration. GEO, Lyngby, Denmark, 2003: 65-88.

[15]YOUNG A G, REMMES B D, MEYER B J. Foundation performance of offshore jack-up drilling rigs[J]. Journal of geotechnical engineering, 1984, 110(7): 841-859.

本文引用格式：

林一，胡安康，蔣瑋，等. 層狀地基中自升式鉆井平臺插樁穿刺風險分析[J]. 哈爾濱工程大學學報， 2016, 37(6): 754-761.

LIN Yi, HU Ankang, JIANG Wei， et al. Risk analysis of punch through for jack-up drilling unit in layered soil[J]. Journal of Harbin Engineering University, 2016, 37(6): 754-761.

收稿日期：2015-03-20.

基金項目：國家自然科學基金項目(51079034).

作者簡介：林一(1984-), 男, 博士. 通信作者：林一, E-mail: linyi1207@163.com.

DOI:10.11990/jheu.201503066

中圖分類號：U661.43

文獻標志碼：A

文章編號：1006-7043(2016)06-0754-08

Risk analysis of punch through for a jack-up drilling unit in layered soil

LIN Yi1, HU Ankang1,2, JIANG Wei1,2, WANG Yitao2

(1. CIMC Ocean Engineering D&R Institute, Shanghai 201206, China; 2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract：When jack-up drilling units are in a preloading condition, it is possible to cause punch-through incidents in layered soils in which there is a stiff layer overlying a weaker layer. This may result in serious structure damage and casualties. Such layered soils are typically of two types-stiff clay/soft clay and stiff sand/soft clay. Taking into account the influence of the soil layer parameters, we used a non-linear numerical method to investigate the change law of the bearing capacity of soil. On this basis, taking a 400-ft jackup drilling unit as an example, we used the Monte-Carlo method, preloading probability distribution, and soil parameters to analyze the risk of punch-through in the Gulf of Mexico.The analysis results show that the risk value is below 10%, Our conclusions can provide a reference for the risk management of similar jackup operations.

Keywords：jack-up drilling unit; punch through; layered soil; risk analysis

網絡出版日期：2016-04-22.