淺談初中生解幾何題能力的培養

陳言光

摘 要： 作者舉中考例題通過解題四個環節：審題、探路、書寫和反思，淺談初中生解幾何題能力的培養。

關鍵詞： 解題能力 幾何題 培養方法

一道初中幾何題不但考查基礎知識點，還考查數學思想、方法，考查學生的解題能力。教學中發現許多學生學習幾何問題用的時間很多，做的題目也很多，但是收到的效果卻不理想，究其原因是他們總是就題論題，費時費力，事倍功半，顯示出學生解題能力低下，因此教師在初中生解幾何題能力方面需要加強培養，根據教學大綱要求，以及觀察初中生解幾何題時的意識、習慣等，筆者淺談初中生解幾何題能力培養方法：

一、審題

審題要求初中生做什么？怎么做？一道幾何題總有若干已知條件和待求解結論，通常還配備幾何圖形，于是，在審題過程中教師應該引導學生做到以下幾點：第一，從題干條件中抓住概念、性質，讀懂題中線段、角的有關數據及各種位置關系、數量關系，關注特殊的點、直線、射線等，結合圖形與題目條件結論進行觀察對照，使題意與圖形在學生印象中正確對應統一。第二，從已有概念、性質進行基本相關聯想，明晰已有線段、角的位置關系和數量關系，將已知條件和待求結論結合，從復雜圖形中分解出基礎幾何圖形，必要時根據題意重新畫圖幫助理解。第三，有些幾何題有許多后續小題，不同小題之間除了原主題干條件相同，前提條件未必相同;相同題干條件下的前面小題的結論又可以作為后續小題的條件。第四，遇上復雜題目，為把握命題者意圖，學生應該將題目多讀幾次，最好逐字逐句分析題意，抓住關鍵字詞深入思考，挖掘隱含條件，為后續解題思路探究鋪平道路，避免“滑過現象”，不可由于審題不認真、不完整導致解題不嚴謹，甚至無從下手。

例1（江西省2016）22.（圖形定義）：如圖，將正n邊形繞點A順時針旋轉60°后，發現旋轉前后兩圖形有另一交點O，連接AO，我們稱AO為“疊弦”;再將“疊弦”AO所在的直線繞點A逆時針旋轉60°后，交旋轉前的圖形于點P，連接PO，我們稱∠OAB為“疊弦角”，△AOP為“疊弦三角形”.

探究證明：

（1）請在圖1和圖2中選擇其中一個證明：“疊弦三角形”（即△AOP）是等邊三角形;

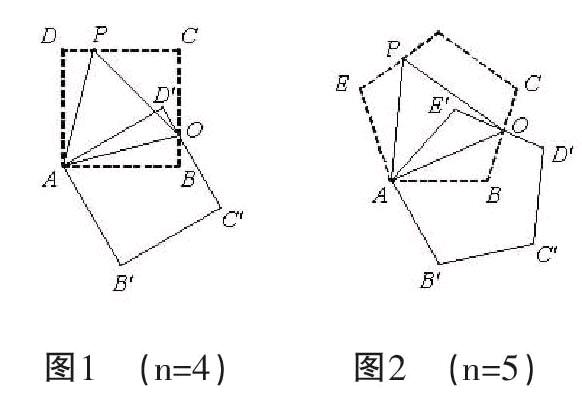
（2）如圖2，求證：∠OAB=∠OAE′.

歸納猜想：

（3）圖1、圖2中“疊弦角”的度數分別為____________________________，__________________________;

（4）圖n中，“疊弦三角形”__________________________等邊三角形（填“是”或“不是”）;

（5）圖n中，“疊弦角”的度數為__________________________（用含n的式子表示）.

粗略地看，題目條件涉及“疊弦”、“疊弦角”、“疊弦三角形”三個新概念，其實際是舊知識，由“將正n邊形繞點A順時針旋轉60°后，發現旋轉前后兩圖形有另一交點O，連接AO”可以在圖形中，找出旋轉前后兩圖形的相對位置，由旋轉性質及正n邊形的各邊相等、各角相等且等于（n-2）×180°÷n，在圖1中明確AD=AD′，∠D=∠D′=90°，由旋轉60°知道各對應點與旋轉中心連線所成角為60°，對應點與旋轉中心的連線段相等，在圖1中明確∠DAD′=60°。根據“再將‘疊弦AO所在的直線繞點A逆時針旋轉60°后，交旋轉前的圖形于點P，連接PO”這個條件，學生容易忽視“AO所在的直線”，從而簡單認為點P與點O是對應點，輕易得出AP=AO，這就是典型的“滑過現象”，目前只有∠OAP=60°是明了的，而AP=AO是否相等憑直覺成立，但需要嚴格推理驗證，由此可見，本題很考驗學生思維的嚴謹性。條件“△AOP為‘疊弦三角形”考查學生理解其產生過程及識圖能力。從第（1）問中，學生應能聯想起等邊三角形的判定定理。第（2）問證角相等，學生除了識別角的位置，認識到角與相關元素的位置及數量關系，及第（1）、（2）問是相同題干，第（1）問中的所有結論可作為第（2）問的前提條件。第（3）問求角度，（1）、（2）、（3）三問發現都涉及圖2，由此，也可以考慮首選圖2解決問題，那么圖1、3、4應當是為幫助理解第（4）、（5）的幾何題規律，便于歸納總結規律而增加的從簡單到復雜、從特殊到一般的圖例。這樣，學生就把握了題意，為探究幾何題的解題思路奠定了堅實的基礎。

二、探路

學生在分析題意，探尋解題思路的過程中應該做些什么？怎么做？筆者認為幾何題以題型而論，可謂種類繁多，幾何題的解題思路需要學生多次探尋，往往也是柳暗花明、精彩紛呈，但多數幾何題的求解或求證，其思路不外乎建立題目已知條件（甚至隱含條件）與所求結論之間的內在聯系，因此，如何將它們聯系起來，是確定解題思路的關鍵。有些幾何題相對簡單，只要根據概念、性質等知識分析其已有條件，就可以很快與結論聯系起來，另有些題目，需要學生將條件與條件結合推理，產生的結論結合其他條件再推理，同時將所求結論不斷轉化，使條件推導得出的結論不斷向所求結論靠攏，所求結論的轉化不斷向已有結論逼近，直至它們在某個點上聯系起來，從而確立解題思路。這就要求學生熟練掌握基礎幾何圖形的概念，性質，并且很清楚它們對應的結論。當解題思路受阻時，用所學知識將條件、結論進行等價轉化，并在某個知識點上“連接起來”，從而打開解題的思維通道，明確解題的思考方向，契合“數學問題一般都是運用學過的知識加以解決”的轉化思想。

例1的思路分析：第（1）問是判定“疊弦三角形”（即△AOP）是等邊三角形，結合已知∠OAP=60°，聯想到等邊三角形判定定理“有一個60°角的等腰三角形是等邊三角形”，接著會想到的是△AOP的哪兩條邊相等？結合“AO所在的直線繞點A逆時針旋轉60°后得到線段AP”，會聯想到AO=AP，但是這兩條線段不能直接相等，需要嚴格證明，以圖1為例，旋轉∠DAD′=∠OAP=60°，得到∠DAP=∠D′AO，四邊形ABCD是正四邊形，可知AD=AD′，∠D=∠D′=90°，兩者結合得△APD≌△AOD′（ASA），到此已經將題目條件與所求證結論聯系起來，問題得解。第（2）問求證：∠OAB=∠OAE′結合題目已知與第（1）問中的結論，容易有兩種常見等價轉化：①證∠OAB=∠EAP，②證△AOB≌△AOE′。思路（一）：第①思路結合已有圖形易聯系起來轉化求證△AOB≌△APE，結合已有直接證明顯得困難，但由第（1）問易得△APE≌△AOE′，兩者合并到思路②，分析已有條件，發現欠缺OB=OE′，觀察OB、OE′是邊BC，D′E′的一部分，且BC=D′E′，于是問題再次轉化為求證OC=OD′，又會有兩個方向：ⅰ）全等三角形對應邊相等，ⅱ）等角對等邊，先探索ⅰ），連接AC、AD′，構造出△AOC和△AOD′，卻依然沒有全等的足夠條件，但可發現對角線AC=AD′，思路到此告一段落，接著探索思路ⅱ），必須連接CD′，要直接得到∠OCD′=∠OD′C，那是困難的，此時結合思路ⅰ）已有的AC=AD′，可以得到∠ACD′=∠AD′C，于是只需∠ACO=∠AD′O，由直覺可以發現只需△ACB≌△AE′D′，到此，已知條件與所求證結論在△ACB≌△AE′D′這個點上建立了聯系，整個解題思路連貫起來，問題得證。思路（二）：第①思路結合已有圖形易聯系起來轉化求證△AOB≌△APE，直接證明欠缺條件，轉而考慮∠PAE=∠OAB亦可，結合圖形易感覺△AOB和△APE存在軸對稱，這就意味著可以在這兩個三角形周邊構造全等三角形，解題策略的通法是將題目中分散的條件集中起來，作AM⊥DE于M，作AN⊥CB于N.得到Rt△AEM和Rt△ABN，以及Rt△APM和Rt△AON，結合以上條件易證這兩對三角形分別全等，推出∠EAM=∠BAN及∠PAM=∠OAN，得證∠PAE=∠OAB，從而解題思路貫通。第（3）問求角的大小，只需結合以上結論與多邊形內角和定理，就可以解決問題。第（4）問可用歸納法，也可以參照以上證法證明之。第（5）問同理第（4）問。

三、書寫

在學生經過認真審題、確定解題思路后，接著就是按照規范的解題格式進行書寫。學生在書寫解答過程中存在字跡潦草、審題不認真、思維混亂、說理無據、思路不清晰、推理不嚴密、解后不檢查等現象，由此可見，教師培養學生規范的書寫解幾何題格式很必要，書寫解答過程要做到表達清楚，層次分明，結論明確，論據充分，目的明確，說服有力，說理有據，做到嚴謹、嚴密、滴水不漏、環環相扣、無懈可擊。第一，教師應該重視培養學生關于文字語言、符號語言、圖形語言三者之間轉化的能力，該能力是準確讀懂題目、圖形，造成對條件、結論、圖形的正確識別、理解、轉換、組織、表達的必備條件，教師在學生探究幾何基礎知識點時，有意識地將一個知識點作為幾何模型讓學生清楚把握結構，將每一個幾何模型中的三種語言之間的轉換做到滾瓜爛熟的地步。第二，要求學生用嚴格的格式、準確數學語言書寫解答過程，教師檢查學生的解題過程，反饋檢查結果，學生及時總結錯誤并訂正，理清書寫要點，歸納解題步驟及注意事項。書寫解題過程是學生理解題意，表達思維過程的外在表現形式，書寫的過程更是學生思維提煉、升華的過程，理解事物本質、抽象概括的過程，是積累研究問題的方法和經驗的重要途徑，因此，應當加強訓練。

例1解：（1）如圖1∵四邊形ABCD是正方形，

由旋轉知：AD=AD′，∠D=∠D′=90°，∠DAD′=∠OAP=60°

∴∠DAP=∠D′AO，

∴△APD≌△AOD′（ASA）

∴AP=AO，又∠OAP=60°，∴△AOP是等邊三角形.

（2）法（一）：如右圖1，連接AC，AD′，CD′，

∵AE′=AB，∠B=∠E′=108°，E′D′=BC，

∴△ABC≌△AE′D′，∴AC=AD′，∠ACB=∠AD′E′，

∴∠AD′C=∠ACD′，∴∠OD′C=∠OCD′，∴OC=OD′，

∴BC-OC=E′D′-OD′，即OB=OE′，

∵AB=AE′，∠B=∠E′，∴△AOB≌△AOE′，∴∠OAB=∠OAE′.

法（二）：如右圖2，作AM⊥DE于M，作AN⊥CB于N.

∵五邊形ABCDE是正五邊形，

由旋轉知：AE=AE′，∠E=∠E′=108°，

∠EAE′=∠OAP=60°

∴∠EAP=∠E′AO，

∴△APE≌△AOE′（ASA）

∴∠OAE′=∠PAE.

在Rt△AEM和Rt△ABN中，

∠M=∠N=90°∠AEM=∠ABN=72°AE=AB

∴Rt△AEM≌Rt△ABN（AAS）

∴∠EAM=∠BAN，AM=AN.

在Rt△APM和Rt△AON中，AP=AOAM=AN

∴Rt△APM≌Rt△AON（HL）.

∴∠PAM=∠OAN，

∴∠PAE=∠OAB，

∴∠OAE′=∠OAB（等量代換）.

（3）15°，24°

（4）是

（5）∠OAB=[（n-2）×180°÷n-60°]÷2=60°-180°/n

四、反思

數學教育家弗賴登塔爾指出：反思是數學活動的核心和動力。學生在解決一道幾何題后應該反思什么？教師應引導學生從題目涉及的知識點、題型結構、類型、條件與結論的關系、題目考察的能力、數學思想方法、解題思路的探索、解法的多樣性、書寫格式的規范性等角度進行反思。如對例1可做如下反思：本題是綜合性較強的一道中考題，涉及的知識點有正n邊形的概念、性質，旋轉的概念、性質，全等三角形的判定、性質，等腰三角形的判定、性質，多邊形內角和公式等。本題屬于探究型幾何題，題干條件復雜抽象，文字繁多，不易理解，條件容易被忽視，使得推理不嚴密，條件與結論看似容易聯系，其實隱含的聯系方式卻相當難找，由此可見本題考查學生文字語言、符號語言、圖形語言三者之間的轉換能力，識圖能力，認真審題習慣，嚴密推理的邏輯思維能力，合情推理能力，觀察分析解決問題能力等。本題主要考查學生轉化思想，從特殊到一般的思想，體現在將所求解（或求證）結論的等價轉化，從正四邊形、正五邊形等一直到正n邊形的求角的大小，同時以上思想就是本題的破解策略，通過條件、結論的各自轉化，最終在某個知識點上建立聯系，從而使解題思路得以貫通。可能出于中考這種限時考察全科的因素，本題書寫規范要求相對降低，如后三個小題以填空形式出現，但學生在平時此類型題目的求解訓練過程中，可以考慮書寫，用于訓練學生的嚴格書寫格式盡量簡化書寫內容，同時培養學生縝密的邏輯推理能力。本題拓展了解法，兩法值得學生借鑒。在本題解答過程中，學生還可能將“圖n”中的n理解為正多邊形的變數，從而產生錯解，因此學生應注意數字與圖形的對應關系。進行解后反思有助于學生積累經驗，鞏固所學知識點，幫助學生總結解題規律，優化解法，達到事半功倍的效果，在已有的基礎上突破、延伸、創新，以應對未知的難題。

最后，教師不可能只利用極少數例子和練習培養學生的解題能力，教師應當為學生提供足夠多的數學問題，使學生視野得以開闊，數學問題的解決過程充滿豐富多彩的觀察、嘗試、歸納、概括的思維活動，在數學學習過程中以問題為載體，感悟數學思維，積累數學活動經驗，提升數學素養，發展學生的數學思維能力，通過數學問題的解決，學生獲取知識的同時，提高解決問題的能力。

參考文獻：

[1]劉華為.從教“怎樣做”到教“怎樣想”.中學數學教學參考（中旬），2016（6）：26-28.