對初中數學課堂案例教學活動實施的認識和思考

呂婷婷

摘 要： 案例教學是初中數學課堂教學的重要環節。案例教學更關注學與教之間的互動、學生能力素養培養及情感情操培樹。本文簡要論述對初中數學課堂實施案例教學活動的認識及思考。

關鍵詞： 初中數學 課堂教學 案例教學

案例是學科知識內容精髓的生動“代言”，是教材學習要求的有效“承載”，更是教師教學目標意圖的重要“展現”。案例教學是初中數學課堂教學的重要環節，也是教師課堂教學的重要任務。案例教學看似對數學問題的講解活動，實際需要綜合多方面教學要素，結合學與教的實際情況，因地制宜，科學施教，是一項系統性的教學工程。近年來，隨著新課程改革的深入推進，初中數學案例教學的要求和標準隨之發生與時俱進的變化。案例教學更關注學與教之間的互動，更關注學生能力素養的培養及情感情操的培樹。筆者以為現行初中數學課堂之中的案例教學活動，將視野放置案例教學的整個全過程，滲透以生為本思想、體現能力培養是第一要務。鑒于上述感知，現簡要論述對初中數學課堂實施案例教學活動的認識及思考。

一、教材要點要義融入其中，體現案例教學的針對性

案例教學是為數學教材教學服務，案例應是數學教材要義的深度概括體和集中展現體。數學案例教學的目的是幫助學習對象鞏固強化對所學數學知識、所獲解析技能的認識和理解。初中數學教師實施案例教學活動時，要將設計數學案例作為首要工程、基礎性工作，把教學意圖、教材內涵等融入數學案例之中，設計的數學案例要具有很強的針對性和代表性，使初中生通過數學案例這一“鏡子”窺探教材知識點的深刻內涵及教學目標要求，從而讓初中生獲得更直觀、更深刻的數學知識內容要義，感受更真切的數學教學目標要求。

如“等腰三角形”一節課案例教學時，教師在案例預設環節根據該節課“經歷剪紙、折紙等活動，進一步認識等腰三角形，了解等腰三角形是軸對稱圖形”、“能夠探索、歸納、驗證等腰三角形的性質，并學會應用等腰三角形的性質”教學目標及“等腰三角形的性質”、“等腰三角形的判定”等知識點的深刻內涵，在此基礎上充分結合以往初中生在該節課學習認知中的實際情況，設計出“如圖所示，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度數”等數學案例。該數學案例的意圖是考查初中生對“等腰三角形的性質，等腰三角形的判定”等數學知識點的掌握和利用情況。初中數學教師通過上述針對性數學案例的有效運用，能夠有效幫助初中生深刻理解和掌握數學知識點內涵，并對其使用注意事項有較為準確的理解和掌握。

二、雙向互動交流滲入其中，體現案例教學的互動性

案例教學作為數學課堂教學的關鍵部分和重要環節，自然秉承數學課堂教學的雙向互動特性。任何學科的教學活動，不是教師或學生“獨自為陣”的單邊個體行動，而是相互貫通、相互配合的協作互動活動。教師和學生只有深入其中，深刻互動、深度配合，才能實現學與教主體和主導特性的有效展現，才能使學與教活動效能的“最優化”。因此，在案例教學中，教師要體現互動特征，雙向特性，將案例講解的過程轉化為師生互動的過程，組織初中生參與案例探析活動，與教師或其他學生個體圍繞案例的解題思路及解答方法等重點環節進行深入討論、交流、溝通等，促使初中生更深入地思考、研析，提升案例教學的實效。

問題：已知一次函數與反比例函數的圖像交于點A（-2，3）、B（m，-2）.（1）求這兩個函數關系式;（2）求該一次函數圖像上到x軸的距離為5的點的坐標;（3）在這個反比例函數圖像的某一支上任取點M（a1，b2）和點N（a1、b2），若a1

初中生個體之間感知問題條件的小組合作學習活動得到其認知體會：該問題主要考查一次函數與反比例函數的關系，特別關于反比例函數與一次函數的交點問題。

教師與初中生圍繞解題要求，共同梳理題意條件關系和內涵，指出：一次函數與反比例函數的解析式可以采用待定系數法、觀察圖像的方法予以解決。在解決第三小問時要充分考慮兩個點所在象限的異同情況。

初中生自主思考探知得到解題思路，教師予以強調，初中生進行思路完善，開展解題活動，過程略。

三、主體參與探析納入其中，體現案例教學的發展性

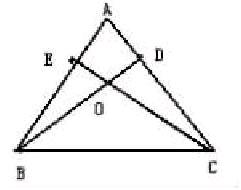
案例：如圖所示，已知△ABC中，AB=AC，BD、CE是高。求證：OB=OC;如果∠ABC=50°，求∠BOC的度數。

初中生解析：結合問題條件及三角形全等的判定定理，可以通過證明三角形全等的形式，求證得到OB=OC。要求∠BOC的度數，可以通過三角形的內角和求得∠A的度數，然后通過四邊形ADOE的內角和得到∠DOE的度數，從而得到∠BOC的度數。

教師點評：該問題主要是運用全等三角形的判定和性質及三角形的內角和定理等。

初中生修正解題思路，得到其思路為：根據題目已知條件可以先證明△ABD和△ACE全等，得到條件進而證明△BOE與△COD全等，從而得到OB=OC。再利用等腰三角形的性質及三角形內角和得到∠A的度數，然后通過四邊形ADOE的內角和得到∠DOE的度數，從而得到∠BOC的度數。

教師組織初中生合作探析歸納解題方法：通常可通過證明三角形全等證明線段相等，計算角度時一般都會利用三角形或者四邊形的內角和性質。

在上述教學活動中，初中生成為案例教學活動的實際踐行者，學生的主體地位得到了盡情的“釋放”，深度參與到了案例講解的全過程，其探究數學的能力、分析思考的能力及推導歸納的能力等得到顯著提升和發展。

由此可見，初中生參與其中的案例教學，貫徹和落實了新課程標準提出的“學生永遠是第一核心，能力永遠是第一要義”的教學要求。教師在具體講解進程中將初中生學習技能錘煉和培養滲透于案例講解中，既要提供初中生進行案例感知、探析、解答的親身實踐活動機會，又要重視初中生探究過程的指導和點撥，保證其探究活動的效果，針對他們解題中出現的認知疑惑、解析困難等情況，予以及時、科學的指導，在推動初中生數學解題進程的同時，實現數學探究分析效能的提升。

總之，初中數學教師在案例教學中只有始終遵循新課程標準，把學生放置于核心地位，凸顯學習能力培養的第一要義，既注重主體的認知、解析訓練，又強化過程的指導和講解，實現案例教學效能的最佳目標。

參考文獻：

[1]樊留榮.初中數學生活化教學案例分析[J].數學學習與研究，2015.

[2]林春安.初中數學數形結合思想教學研究與案例分析[J].讀寫算（教研版），2015（12）.