管中窺豹可見一斑

張大偉

【摘 要】今年的中考試題仍注重對雙基的考查，大部分題型來源于教材，貼近初中數學的教學實際，知識點的考查既全面，又突出重點，注重對初中數學中蘊含的數學思想方法和學生思維能力的考查。本文著重分析了2016年數學中考試卷命題的特點，并由此帶來對教學的啟發。

【關鍵詞】中考數學；試卷命題；特點分析；啟發

一、試卷特點分析

1.回歸課本，考查考生的雙基水平。

例如，（試卷第9題）分解因式2a（b+c）-3（b+c）的結果是______。

評析：本題考查了因式分解，應用提公因式法即可解題。

2.關注生活，讓數學有教育意義。

例如，（試卷第1題）為了方便市民出行。提倡低碳交通，近幾年南京市大力發展公共自行車系統。根據規劃，全市公共自行車總量明年將達70 000輛。用科學計數法表示70 000是

A.0.7×105 B.7×104 C.7×105 D.70×103

評析：本題考查了科學記數法，科學記數法的表示形式為a×10n形式，其中1≤|a|<10，n為整數，70000=7×104。故選B。此題題目雖簡單，但它取材于生活，又應用于生活，提倡“低碳交通”，具有教育意義。

3.注重學習過程，促進學生發展。

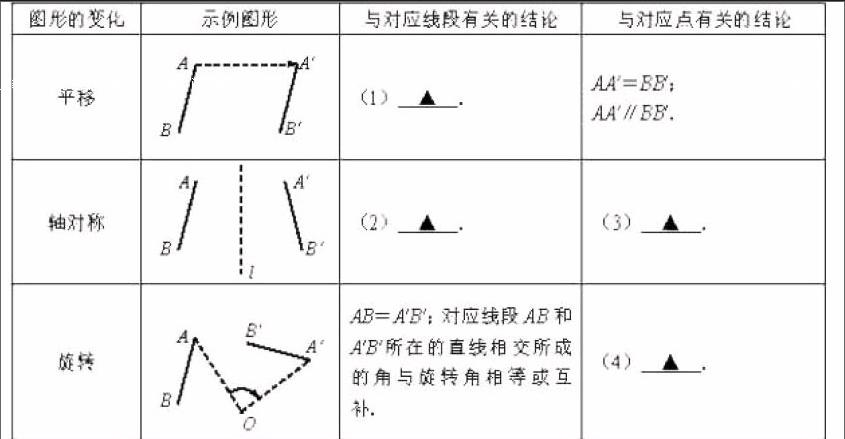
例如，（試卷第20題）我們在學完“平移、軸對稱、旋轉”三種圖形的變化后，可以進行進一步研究，請根據示例圖形，完成下表：

評析：本題主要考查了整個初中階段學生對平移、軸對稱、旋轉這三種圖形變化的掌握情況，注重學生在學習中數學活動經驗的積累，需要學生既要重視學習結果也要重視學習過程。

4.穩扎穩打，注重對考生基本能力的培養。

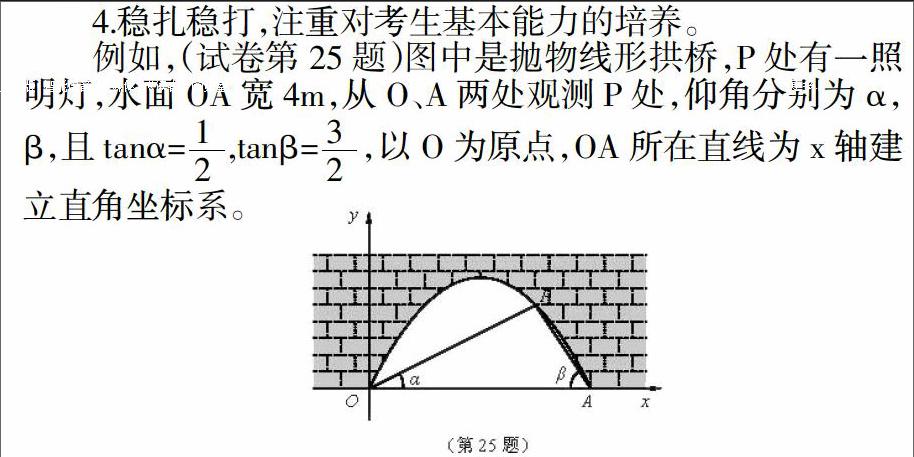
例如，（試卷第25題）圖中是拋物線形拱橋，P處有一照明燈，水面OA寬4m，從O、A兩處觀測P處，仰角分別為α，β，且tanα=，tanβ=，以O為原點，OA所在直線為x軸建立直角坐標系。

（1）求點P的坐標

（2）水面上升1m，水面寬多少（取1.41，結果精確到0.1m）？

評析：本題題目比較新穎，將三角函數和二次函數有機地結合起來。通過設置應用性，信息性，實踐操作性的試題，既讓學生獲取了數學信息，又很好考查了學生應用數學知識解決實際問題的能力。

二、由中考試卷命題特點得到的教學啟發

1.以教材為中心，夯實的數學基礎。對于認真研究近年的南京中考數學試卷的老師來說，教材中定理證明、例題、習題就是中考試題的“根”，有些試題在教材中能找到原型，有些試題則是對教材例題、習題基礎上加工改編、改變條件、延伸或擴展而成的，換句話來說，教材中的定理證明、例題、習題為編制中考數學試題提供了豐富的資源。因此，我們數學老師必須認真研讀教材和新課程標準，重視對基礎知識的教學，決不能眼高手低。

2.學以致用，增強學生應用數學的意識。學習數學的最終目的就是應用，因此我們數學老師在平時的教學、作業設計以及試卷編制時要有意識地呈現一些能夠聯系生產、生活的實際，貼近生活，貼近學生實際，有教育意義的情景作為背景的數學例題或者試題，引導學生學會觀察生活、關注生活、將實際問題抽象成數學問題，建立數學模型，并進行解釋與應用。這樣能夠引導學生在問題解決中，體會數學與人類社會的密切關系，增進對數學本質的理解。

3.注重學習過程，培養學生的數學基本能力。蘇科版教材中有“數學實驗室”這一環節，經常需要我們老師與學生一起經歷數學問題的探索過程，有的時候因為缺少數學活動的道具，有的時候因為要趕教學進度，不如多講幾個課外題的僥幸心理等原因，讓我們忽視了學習過程。這次中考第21題，如果我們不重視學生學習過程的積累，必然會導致學生的得分率會很低。以此題為載體，我們今后要讓學生積極參與數學思維活動、經歷知識產生發展過程。做題時不能就題論題，要學會舉一反三，變換試題條件，重視一題多解的能力，研究與其他題目的聯系與區別，挖掘出其中蘊涵的數學思想方法，掌握數學本質。

4.教會思考，使學生養成獨立思考的習慣。曾經聽過一個講座，給我們做講座的學者問過一個問題：我們到底要教給學生些什么？ 知識、方法還是能力？ 通過學習與思考，我覺得數學教學的本質應該是教會學生數學思考。那么在平常的教學中，我們需要做好以下三點：①激發思考的欲望，明確思考的目標，讓學生認識到思考的重要性；②提供適量的思考依據，也就是要讓學生如何思考，能靈活恰當的找到思考的依據；③要留有充裕的思考時間，讓學生養成良好的聽課習慣，鼓勵學生獨立思考，不能在課堂上因過分炫耀而失去思考的機會，也不能因為問題難而放棄思考。

【參考文獻】

[1]徐駿.注重基礎，穩中求新，凸顯能力[J].中學數學，2011.6

[2]李青.數學教學的本質：教會學生思考[J].《素質教育》，2012年7月總第89期