初中數學“圖形與幾何”中的合情推理研究

石小江

[摘 要] “圖形與幾何”是初中數學課程中的一個重要的知識點. 隨著新課程教育教學的改革，傳統的演繹推理教學法已經不再適用于當前初中數學教學. 對此，發展合情推理的教學方式來進行初中數學“圖形與幾何”的教學十分有必要.

[關鍵詞] 初中數學；圖形與幾何；合情推理；研究

“圖形與幾何”這一部分內容是初中數學重點的教學內容，同時也是初中數學最基礎的教學內容. 傳統的初中數學課堂教學的過程中，通常情況下都是讓學生不斷進行習題訓練來促使其掌握相關的數學知識與內容. 這種教學方式在“圖形與幾何”這一部分的教學中存在著明顯的不合理現象，從而導致初中生的數學成績無法得到有效提升，使得學生對初中數學知識沒有學習的興趣，學習效率十分低下. 據此，初中數學教師需要結合新課程教學改革的相關內容以及初中生的實際學習情況來采取合情推理的方式開展“圖形與幾何”的教學，提升學生的學習效率.

合情推理的意義

合情推理就是從已知的事物出發，在一定的情境中依據相關的經驗，采用類比的方法進行歸納，進而得出可能的某種結論. 合情推理是以發現為核心內容的，進而激發學生合情推理的能力，增加學生進行知識創新的意識與能力. 由于初中是數學知識進行教育與培養的重要時期，對學生思維及分析能力的培養十分關鍵. 據此，通過應用合情推理的教學模式，能夠有效地提升初中生思維跳躍的能力，激發學生的學習思維. 因此，在“圖形與幾何”的教學中采用合情推理的教學模式能夠合理構建相關的幾何圖形，通過相關的思維及邏輯的分析，進而對初中生進行邏輯思維能力的培養.

當前我國初中數學幾何教學的

現狀

幾何教育是初中數學教育的重要組成部分，通過幾何知識的學習能夠有效地提升學生的邏輯思維以及演繹推理的能力. 但是就目前我國的教育體制來看，受應試教育的影響，初中數學教師在課堂教學的過程中只要求學生記住相關的概念、數學公式、幾何知識等，通過給學生布置大量的幾何練習來開展教學. 但是這種題海戰術使得學生產生了對數學課程厭煩的情緒，造成初中生的數學學習效率較低. 通常情況下，幾何課程教學能夠分為演繹推理以及合情推理這兩種方法. 其中的演繹推理是從一般性的原理出發，進而推導出某種情況下的結論，應用于大多數數學知識的課堂教學. 而合情推理還可以分成歸納推理和類比推理，通常都是從部分向整體、個別到一般的方式來進行推理的，能夠對初中生的創新思維進行有效地激發與培養.

“圖形與幾何”中的合情推理

模式

1. 直觀幾何

直觀幾何就是以直觀觀察為主的一種幾何圖形. 老師及學生能夠通過自身的經驗來對圖形進行觀察并獲得相關的信息，通過對這些信息進行有效地探究與測試，與其他的事物相聯系、尋求其間的關系等方式來解決實際問題. 初中數學中的幾何圖形就是對客觀現實事物的一種抽象的表示，擁有著極強的直觀性特點. 同時，這些教學的內容與初中生的實際學習及生活的情況相適應，能夠增加初中生的學習興趣，幫助學生更好地進行學習. 在初中數學課堂上，教師通過引導學生觀察幾何圖形，并從中發現相關的問題、解決問題來進行教學，同時還能夠激發初中生聯想與想象的能力.

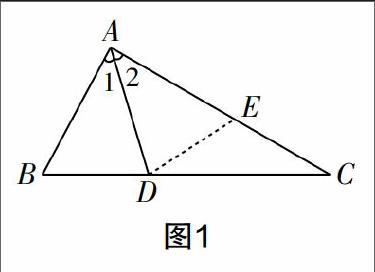
例如：如圖1所示，在△ABC中，∠B=2∠C，其中∠A的平分線為AD，求證：AB+BD=AC.

這道題就是將結論給出，讓學生通過應用相關的知識來證明結論的準確性. 需要學生在做題的時候具備合情推理的能力，能夠進行反向推理. 因此，想要證明AB+BD=AC是正確的，則需要先證明AC-AB=BD. 對此，可以在三角形中作一條輔助線，即在AC 邊上取點E，使得AB=AE，這樣就只需要證明出BD=EC. 因為AD為∠A的角平分線，此時只需要證明DE=CE即可解決該問題. 依據這種思維及思考的方法能夠從直觀的角度來進行思考，進而有效地激發初中生思維與聯想的能力.

2. 歸納推理

在初中數學的教學過程中，歸納推理是一種對問題進行全面、綜合分析的方法，一般情況下包含兩個方面的內容，即由一類事物中的特殊情況向一般性進行推理，以及通過對相關的經驗和觀察的結果進行歸納與推理，從而達到去粗取精的效果.

例如：在研究“多邊形的內角和定理”的時候，通過已知的三角形內角和為180°以及相關對角線的知識，可以引導學生通過對三角形的相關結論進行分析與觀察，來總結與歸納四邊形、五邊形、六邊形等的內角和度數. 同時還可以引導學生進一步觀察與分析多邊形內角和的共性，學生就能夠順應教師的思路與思維自然地推算出n邊形的內角和度數為（n-2）×180°. 這種方法就是歸納推理的方法，通過這種方法的教學與研究，能夠幫助初中生更加深刻地理解多邊形的內角和定理，幫助初中生更好地、更深刻地理解與記憶，同時還能夠有效提升初中生推理及歸納的能力.

3. 類比推理

在初中數學“圖形與幾何”的教學過程中，應用類比的方法也是合情推理的一個重要方式. 在進行類比推理的過程中，主要依據的是相關的屬性，通過對某種事物的屬性進行研究，進而合情合理地類比推理出相關事物的屬性特征.

例如：在“多邊形內角和”的教學過程中，通過對三角形內角和進行復習，而后通過三角形的相關定理及性質推導出四邊形的相關定理及性質. 已知三角形的內角和為180°，可推導出四邊形的內角和為360°. 通過這種類比推理的方法能夠幫助初中生更快地接受與原有知識相類似的數學知識，進而通過分析與比較就可以得出相關的概念及理論，促使學生更好地學習與理解幾何知識的相關內容，提升數學學習的知識與能力.

“圖形與幾何”中合情推理的教

學方法

1. 吸引學生的學習興趣

在初中數學“圖形與幾何”的教學內容中，所涉及的知識點包括點、線、面三部分的內容. 由于這些內容具有一定的抽象性，因而學生們在學習的過程中會覺得難度較大，加之傳統的教育教學方式還使得學生失去了對這些內容的學習興趣. 對此，通過應用合情推理的方法來進行初中數學教學，能夠有效激發學生的學習興趣，幫助學生更好地理解“圖形與幾何”中的相關內容及知識點. 教師可以通過讓學生對相關的圖形進行觀察，并依據圖形的形狀及大小來引導學生進行類比與推理，總結出相關的性質及規律. 這種課堂教學的方式能夠有效地提升初中生對數學知識的學習興趣，提升課堂教學的效率.

2. 創設教學情境

在初中數學的課堂教學過程中，通過創設課堂教學的情境能夠促使合情推理教學的開展與實施. 教師通過創設和“圖形與幾何”相關的課堂教學情境，能夠幫助學生抓住相關幾何圖形的本質特征，進而更加深刻地理解相關的內容與知識，靈活地運用相關知識及理論. 此外，通過創設教學情境，教師就能夠引導學生依據已知的條件進行分析與推理，發現其中隱藏的重難點，依據自身的想象與假設來進行分析與推理，由此就能夠有效地提升初中生對問題的理解及分析能力.

結語

隨著時代的發展以及教育體系改革的不斷推進，傳統的初中教育方式存在著很多的弊端與缺陷，已經不再適用于現今“圖形與幾何”的教學. 據此，初中數學教師需要根據學生的實際情況，在“圖形與幾何”的教學中應用“合情推理”的教學方法來開展教學. 以此來有效地提升初中生對抽象幾何圖形的理解能力，激發學生的學習興趣，引導學生采用推理、類比的思維進行數學的學習，進而能夠有效提升數學課堂教學的效率，增加學生的學習興趣，提升學生的數學學習成績.