發展幾何直觀 提升數學素養
雷梅玲


【摘要】發展學生的幾何直觀能力能讓學生從具體對象背后發現抽象的數學本質,對學生思考數學問題、發展數形結合思想起到關鍵的作用,是學生必備的一種基本數學素養。學生在親歷操作活動之后,獲得的經驗將更加真實豐富,有助于增強學生的幾何直觀意識,積累數學思維活動經驗,發展數學思維能力,提升學生的數學素養。
【關鍵詞】幾何直觀;數學素養;意識;表象;能力
《義務教育數學課程標準(2011版)》指出:“幾何直觀主要是指利用圖形描述和分析問題。借助幾何直觀可以把復雜的數學問題變得簡明、形象,有助于探索解決問題的思路,預測結果。” 可見,幾何直觀能力是空間觀念形成的基礎。在小學階段,學生的思維特點以具體形象思維為主,逐步向抽象邏輯思維能力發展,發展學生的幾何直觀能力恰好能讓學生從具體對象背后發現抽象的數學本質,對學生思考數學問題、發展數形結合思想起到關鍵的作用,是學生必備的一種基本數學素養。那么如何發展幾何直觀,提升學生的數學素養呢?
一、親歷操作探索的過程,增強幾何直觀意識
史寧中教授說:“從某種意義上說,幾何直觀就是數學活動經驗(實踐經驗和思維經驗)不斷積累所形成的數學素養。”而數學活動經驗的獲得需要親手觸摸,直觀感知,切身體驗。因此,培養學生的幾何直觀能力必須加強學生的實踐操作活動,提高學生的動手能力。在小學圖形與幾何領域的教學中,往往需要學生借助實物、模型等進行動手操作活動,親身經歷摸一摸、看一看、拼一拼、比一比、做一做等活動來獲得感知,調動多種感官的參與,在頭腦中逐步建立事物的表象,在直觀的操作活動中慢慢凸顯幾何圖形的特征,發現數學的本質。
例如,在教學“毫米的認識”中,先讓學生用直尺測量書本的長和寬,發現寬是18厘米多一些,引發學生要想知道具體是多少應該用到新的度量單位——毫米。為了幫助學生建構1毫米的模型,讓學生量一量、比一比1分硬幣的厚度,初步感知1毫米。在對物體進行分類活動中,讓學生找出哪些物品的厚度是1毫米,哪些物品的厚度大于1毫米,哪些物品的厚度小于1毫米,分類后要求學生用合適的方法進行驗證,學生就能通過剛才活動獲得的經驗用1分硬幣作為參照物或用直尺測量來驗證,進一步建立和鞏固1毫米的概念。又如教學“角的初步認識”中,創設扇子打開、剪刀打開、時鐘轉動的動態情境,引導學生從這些實物中抽象出數學的角,發現角的產生過程。在對角有了初步感知后,讓學生從三角板上找靜態的角,幫助學生建構角的特征和概念,最后通對魔術棒的操作,感受到角的大小。
學生在親歷操作活動之后,獲得的經驗將更加真實豐富,有助于增強學生的幾何直觀意識,積累數學思維活動經驗,發展數學思維能力,提升學生的數學素養。
二、親歷知識獲得的過程,積累幾何直觀表象
表象是幾何直觀思維的基礎元素。在實際教學中,學生對幾何圖形知識的獲得是需要一定過程的。這就要求教師充分了解學生“最近發展區”,利用學生已有的知識和經驗結合具體的內容設計相對應的數學活動,可以是靜態的觀察思考過程,也可以是動態的動手操作過程,讓學生經歷幾何知識產生的過程,幫助學生豐富幾何表象。學生在大量的觀察、思考、比較、分類等活動過程中積累的幾何直觀表象越豐富,越容易把抽象的數學問題轉化成直觀的表象。這樣有利于發現數學本質,真正掌握數學知識,提升幾何直觀素養。
例如在教學“長方形的面積”時先出示圖①,引導學生可以用1平方厘米的小正方形進行測量,學生發現用全部擺滿(如圖②)和不擺滿(如圖③)可以算出長方形的面積。學生經歷直觀操作已經把抽象的數學問題具體化。然后再引導學生發現利用圖②與圖③之間的聯系也可以用每行的面積個數乘每列的面積個數得到長方形的面積,又為后面公式與擺面積單位溝通了內在聯系。在計算圖④和圖⑤兩個長方形的面積時,學生就能運用不擺滿的方法進行測量,再次豐富了思維經驗。
學生在動手操作中掌握用1平方厘米的面積單位來測量,經歷用面積單位測量長方形的面積,建立和深化面積意識。這時出示表格(如表1),通過表格的數據,學生聯系數面積單位個數的經驗很快就發現長方形的面積=長×寬,然后借助1平方厘米小正方形測量三個長方形面積的過程引導學生發現每一個長方形的長和寬的長度與擺的面積單位之間的聯系。以圖⑤為例,教學中引導學生發現每個1平方厘米的小正方形的邊長是1厘米,這個長方形的長擺了4個1平方厘米的小正方形,長就是4厘米,寬擺了3個1平方厘米的小正方形,寬就是3厘米,(出示圖⑥)。通過前面長方形方面積等于每行擺的面積單位的個數乘每列擺的面積單位的個數可以得出長方形的面積等于長乘寬。
通過一系列的數學活動過程,學生發現長方形長和寬的長度與面積單位個數的關系,再找到面積與長、寬之間的關系,親歷知識的形成過程,突破由面積單位到長度單位的轉化這一理解難點,推進思維發展,深化理解面積計算方法,積累長方形面積的表象,發展幾何直觀,提升數學素養。
三、親歷遷移運用的過程,發展幾何直觀能力
遷移與聯想、想象有一定的聯系。聯想與想象是拓展學生幾何直觀思維空間的主渠道,讓學生經歷知識遷移運用的過程是發展學生幾何直觀能力的重要手段。數學的學習不僅是讓學生獲得知識,更重要的是讓學生以已有的知識和經驗為起點,經歷操作、思考,得出新的數學知識,建構新的數學模型。教學中,教師應該善于引導學生發現新舊知識之間的聯系,通過聯想與想象自主獲得新的數學知識,從而在活動中獲得基本的活動經驗,不斷發現問題,解決問題,提高幾何直觀能力。
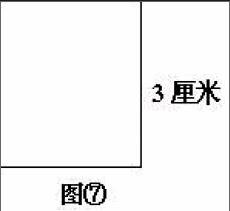
例如教學“長方形的面積”探索正方形面積時(出示圖⑦),要求學生利用探索長方形面積公式的方法自主探索正方形的面積公式。因為知識的遷移運用,學生很容易把探索長方形面積的方法運用在正方形面積公式的推導上。具體會出現以下三種探究的過程:一是用擺一擺的方法,每行可以擺3個1平方厘米的小正方形,每列也可以擺3個1平方厘米的小正方形;二是根據正方形的邊長是3厘米,可以擺3個邊長1厘米的小正方形,每個擺3個,可以擺3行,一共是9個邊長1厘米的小正方形;三是利用正方形是特殊的長方形,把這個正方形看成長方形,長和寬都是3厘米,根據剛才長方形的面積等于長乘寬,推導出正方形的面積就等于邊長乘邊長。
又如,教學“有趣的測量”時,先呈現長方體、正方體、石塊、橡皮泥、土豆等物品,學生利用已有知識就能判斷長方體和正方體可以用公式來解決,石塊、橡皮泥、土豆是不規則物體,不能用公式解決。接著讓學生動手捏一捏,體會到橡皮泥可以通過捏成長方體或正方體的轉化過程算出體積,石頭不能捏,需要通過其他方法來進行測量,產生認知沖突,意識到必須思考新的解決問題策略。為了解決新的問題,教師繼續組織學生根據自己的思考與經驗來總結出實驗所需要的材料、步驟、注意事項等,然后再進行分組實驗。學生在分組實驗中探尋不同解決問題的方法,在活動中感悟到雖然實驗的過程不一樣,但所運用的方法都是經歷將不規則物體體積轉化成規則物體體積進行測量計算的方法。
總之,學生數學素養的形成是一個長期的、不斷體驗的、慢慢積淀的過程。在數學活動中,教師應更多關注如何挖掘數學知識本身的內涵,建立具體形象的事物與數學知識本質之間的聯系,學會用幾何直觀解決數學問題。當學生的體驗豐富了,經驗的積累也就相應地增加了,就能生動形象地描述幾何圖形的問題,積累表象,展開豐富的聯想與想象,經歷“做數學”和“思考數學”的過程,從“經歷”走向“經驗”,將數學素養的形成真正落實到課堂教學并有效地融入學習過程中,持之以恒,學生的數學素養就能真正得到培養和提升。
【參考文獻】
[1]中華人民共和國教育部.義務教育數學課程標準(2011年版)[M].北京:北京師范大學出版社,2012.
[2]李凡國.第一學段學生幾何直觀能力的培養[J].教學與管理,2017(08):46-47.
[3]楊豫暉.義務教育課程標準(2011年版)案例式解讀:小學數學[M].北京:教育科學出版社,2012:47-48.endprint

