應用型人才培養模式下《復變函數》課程可視化教學實現

王日棟，湯 獲，李書海，敖 恩，周海燕，劉春輝

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

應用型人才培養模式下《復變函數》課程可視化教學實現

王日棟，湯 獲，李書海，敖 恩，周海燕，劉春輝

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

《復變函數》是數學與應用數學專業的一門重要基礎課，其在講授和理解上都很困難.本文基于MATLAB的工具包，將某些初等函數圖像具體化，同時對留數與積分計算也進行了簡單探討，有助于學生對本課程的理解和掌握，也能夠提升學生的學習興趣.

復變函數；可視化；MATLAB；教學

《復變函數》是數學與應用數學專業的基礎課程，也是物理、電子、地質等多個學科的重要專業課程.復變函數就是自變量為復數的函數，在某種意義下可導的復變函數稱為解析函數[1].復變函數的自變量和因變量都是復數，它在某些方面有著與實變函數截然不同的特征，如負數可以開偶次方及計算對數，對數函數和根式函數都是多值函數，正弦函數和余弦函數的模不但可以大于1，而且是無界的等，這使得復變函數在教師講授和學生理解上都很困難，因此，我們需要借助函數的圖像來幫助我們理解.由于復變函數的實部和虛部為二元實函數，所以需要在四維空間中描繪其圖像.MATLAB作為強大的數學輔助工具可以很好地實現.若用x軸和y軸分別表示自變量的實部和虛部，用z軸表示因變量的實部，就能刻畫三維空間圖像；若再用曲面的顏色代表因變量的虛部，這樣就能刻畫四維空間圖像.

1 函數圖像的描繪

在MATLAB2014中，我們可以用簡單的命令來畫出基本初等函數的圖像，以描繪指數函數圖像的M文件為例：

x=[-4*pi:pi/15:4*pi];

[x,y]=meshgrid(x);

z=x+i*y;

u=exp(z);

surf(x,y,real(u),imag(u));

hold on;

colorbar('vert');

title('u=exp(z)').

描繪不同的函數圖像時只需要將語句u=exp(z)轉換成相應的函數語句即可，如正、余弦函數分別可以寫成u=sin(z)、u=cos(z).

1.1 單值復變函數—正弦、余弦函數

對于余弦函數f(z)=cos(z)，其代數形式可以表示為：

而正弦函數則可以表示為：

圖1和圖2分別表示半徑為5的余弦函數圖像以及其實部圖像.圖3和圖4分別表示半徑為5的正弦函數圖像及其實部圖像.從解析表達式上可知余弦（正弦）函數為單值函數，其實從其圖像上也可以看出.從余弦（正弦）函數的解析式以及復數模的計算方法可知余弦函數的模是可以大于1的.

圖1 |z|=5時的余弦函數圖像

圖2 |z|=5時的余弦函數實部圖像

圖3 |z|=5時的正弦函數圖像

圖4 |z|=5時的正弦函數實部圖像

1.2 多值復變函數—對數函數、根式函數

復數范圍內的對數函數log(z)的表達式為：

f(z)=log(z)=log|z|+i(θ+2nπ)(n=0,±1,±2…)，其與實數范圍內對數函數的差別主要有兩點：（1）負數的對數是有意義的，即使虛部為零時，若z=x，當x為負數時，z的對數也是存在的.（2）對數函數是多值函數，其原因是輻角的多值性，這一點從表達式上也可以得到體現.對數函數的實部仍然是單值函數，但其虛部對應于復平面內一點存在無窮多個值，相鄰之間相差2π.圖5給出的是對數函數log(z)的圖像，圖6給出的是對數函數log(z)的實部圖像，圖7顯示出的是對數函數log(z)的多值性，我們給出了4個值作為代表.

圖5 對數函數的圖像

圖6 對數函數的實部圖像

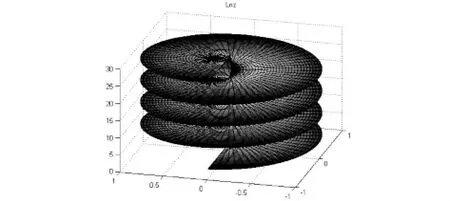
圖7 對數函數的多值性（4個值）

圖8 根式函數的圖像

圖9 根式函數的實部圖像

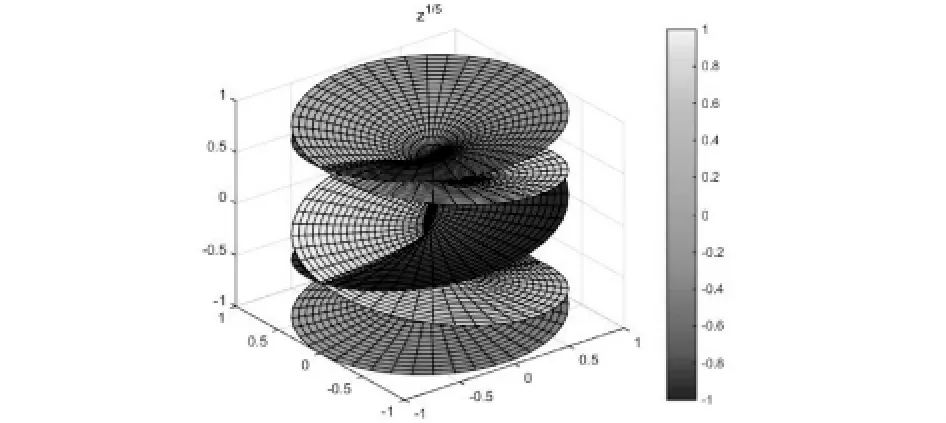
圖10 根式函數的圖像

其中的θ為輻角主值，從表達式可以看出根式函數的多值性主要是由于輻角的多值性.圖8和圖9分別給出了根式函數的圖像及其實部圖像.從圖8我們可以看出對于每個自變量，都有兩個因變量與其對應；當n=5時，從圖10可以看出每個自變量對應5個值.

2 留數與積分計算

2.1 留數計算

復變函數中的留數計算是一個難點，極點的位置不同、階數不同都影響留數計算.針對極點的不同情況進行分析，應用MATLAB提供不同的計算留數語句及方法來進行處理.將需要計算留數的解析表達式f(z)用f表示，當z0為一階簡單極點時，我們可以用命令R=limit(f*(z-z0),z,z0)來計算，當z0為m階簡單極點時，我們需要將命令語句改寫成如下的形式：R=limit(diff(f*(z-z0)^m,z,m-1)/prod(1:m-1),z,z0).如果解析表達式f(z)僅為簡單極點的有理函數，我們還可以通過命令[R,P,K]=residue(B,A)來計算，其中向量B為表達式f(z)的分子系數，A為表達式f(z)的分母系數，命令的返回值有三個，分別是留數向量R，極點位置P和表達式f(z)的直接項K.

分析：法一：應用limit命令.

從題知可知，z=1和z=-1分別是函數f(z)的一階極點和二階極點，應用MATLAB計算留數時需要用不同的語句.建立M文件如下：

syms z;

f=z/(z-1)/((z+1)^2);

R1=limit(f*(z-1),z,1);

R2=limit(diff(f*(z+1)^2,z,1)/prod(1:1),z,-1),

運行結果為R1=1/4；R2=-1/4，與理論計算結果相同.

法二：應用residue命令.

編寫M文件如下：

clear;

syms z;

A=[1,0];

B=[1,1,-1,-1];

[R,P,K]=residue(A,B),

方法二的好處在于一次性可以計算出所有極點及其留數，不用考慮極點的多重性，但其限制也是明顯的，只能用于有理表達式中.

分析：此題中函數的分子為指數函數，不能應用residue語句，只能用limit語句，編寫M文件，分別計算當z=πi和z=0時的留數，結果如下：

R1=1/(6*pi^2)+i/pi^3-3/pi^4-(4*i)/pi^5;

R2=1/pi^4-(4*i)/pi^5.

2.2 用留數計算積分

計算出函數的留數以后，應用留數定理計算復變函數積分就變得相對簡單了.分析所求積分區域內所包含的極點，對每一個極點計算出相應的留數，再用留數定理可得積分結果為S=2πi(sum(R))，sum(R)表示各極點留數的和.

分析：通過分析我們知道該積分具有4個極點:-i,1,3,∞，而在區|z|≤2內只有兩個極點-i,1，因此只需要計算出這兩個極點的留數，再應用留數定理即可計算出該積分.應用MATLAB編寫M文件如下：

clear;

syms z;

f=1/(z+1i)^10/(z-1)/(z-3);

r1=limit(diff(f*(z+1i)^10,z,9)/prod(1:9),z,-1i);

r2=limit(f*(z-1),z,1);

S=2*pi*1i*(r1+r2),

即可計算出積分的值S=pi*(237/312500000+(779*i)/78125000).該積分的理論解為整理后可知其與MATLAB計算出來的結果精度在10-20以上，這個精度對一般工業生產、日常生活已經足夠了，故對于MATLAB的計算結果我們認為是可以采用的.

3 輻角的計算

眾所周知，復數的輻角具有多值性，這就使得很多復變函數具有多值性，這也是復變函數和實變函數的本質區別之一.如何將初等多值函數分解成單值函數也就成為了復變函數的教學難點之一.為了解決這一難點，我們必須徹底弄清輻角函數.在文獻[4][5]中，作者對輻角函數的性質進行了系統的挖掘和總結.

在MATLAB中求輻角的標準函數angle(z)，其意義是給出復數z的輻角，但實際上它能顯示的是復數z的輻角主值，且是用實數表示的，范圍為-π＜angle(z)≤π，例如 angle(1+i)、angle(-i)、angle(-1)的運算結果分別為是0.78543.1416（π）.

由文獻[1]可知，我們可以得到復數在做乘法和除法時的輻角變化過程.由歐拉公式可得，任意復數z=x+yi(x,y∈R)都可以表示成指數形式z=er+iθ=ereiθ，且不難驗證

和

成立.從上述公式我們可以看出輻角的變化具有明顯的幾何意義，即復平面內向量z1和z2的夾角變化，當函數做乘法時為輻角的和，做除法時為分子函數與分母函數的輻角之差.當這個夾角變化不超過主值的規定范圍時，我們可以用標準函數angle(z)來計算.

clear;

z1=1+i;

z2=i;

angle(z1/z2);

例5 計算(-1+i)×(-i)的輻角.

4 結論

復變函數作為數學專業的一門重要基礎課，學生的學習和掌握程度對其在今后的學習過程中會產生重要影響，因此，我們要做好講授工作.復變函數的可視化可以將難于理解的知識用四維圖像的形式清晰地展現出來.本文利用MATLAB給出了單值的余弦函數圖像、多值的對數函數圖像，有助于學生能夠直觀地理解重難點知識.復變函數的可視化不僅有助于學生對書本知識的掌握，也可以提高學生學習的熱情，在今后的教學過程中應不斷深入研究提高，更好地提高教學質量.

〔1〕鐘玉泉.復變函數（第四版）[M].北京：高等教育出版社,2013.

〔2〕徐彬.Matlab在復變函數與積分變換課堂教學中的應用[J].湖北理工學院學報,2016,32(3):68-72.

〔3〕朱建民,李穎.復變函數的可視化問題[J].大學數學,2011,27(1):175-178.

〔4〕金庭枝,王長慶.多值函數的單值解析分析[J].遼寧師范大學學報（自然科學版）,2000,23(2):217-219.

〔5〕王金花.一類多值函數的單值解析分支[J].滄州師范學院學報,2016,32(1):17-19.

O174.5-4

A

1673-260X（2017）10-0004-04

2017-08-12

赤峰學院教學改革研究項目(JGXM201617)