初中數(shù)學理解性教學實驗研究

吳娟

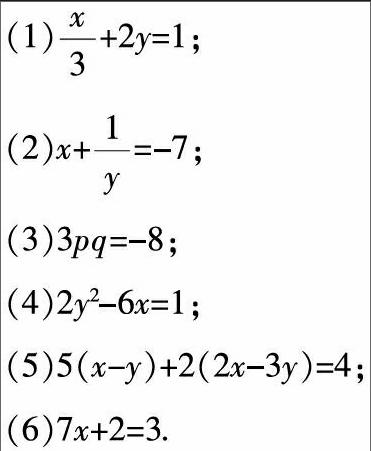
[摘 要] 教師在引導學生學習知識時，不能僅僅只是引導學生機械地記憶知識，還應引導學生深入地理解知識. 本文說明教師開展理解性教學實施的方法，只要教師應用這樣的方法開展教學活動，就能讓學生從抽象的角度看待知識、理解數(shù)學問題產(chǎn)生的機理、能根據(jù)數(shù)學問題的規(guī)律推測問題可能產(chǎn)生的變化，從而能靈活應用知識.

[關(guān)鍵詞] 數(shù)學教學；理解性教學；二元一次方程

教師應用理解性教學來引導學生理解知識，是指教師通過教學活動使學生能從抽象的角度看待知識、理解數(shù)學問題產(chǎn)生的機理、能根據(jù)數(shù)學問題的規(guī)律推測問題可能產(chǎn)生的變化. 學生只有深入理解了知識，才能靈活地應用知識，深入理解知識是應用知識的基礎(chǔ).

引導學生在遷移中理解知識

學生理解知識時遇到的困難之一，就是覺得知識太陌生，他們不能迅速理解. 當學生在學習時感受到學習障礙，并且認為可能不能克服學習障礙時，就容易喪失學習知識的興趣，不愿意再探索及理解知識.

教師在開展數(shù)學教學時，要幫助學生克服學習障礙，幫助學生找到學習知識的信息. 學生在課堂上、生活中已經(jīng)有了一些知識經(jīng)驗，教師如果引導學生把新知識與舊知識結(jié)合起來，讓學生以舊知識為基礎(chǔ)，理解新知識的機理，就能讓學生迅速理解新知識.

現(xiàn)以教師引導學生理解二元一次方程式為例. 一位教師在引導學生學習二元一次方程式以前，先引導學生思考一個問題：

小紅去水果店買西瓜，她共花了18.2元買了10斤西瓜，你知道西瓜的單價是多少嗎？請應用方程的形式解這一個數(shù)學問題.

對學生來說，這是一道不難的一元一次方程問題. 學生們列出方程式：設一斤西瓜為x元，西瓜單價和總價的關(guān)系為10x=18.2，解之得x=1.82，即西瓜的單價為1.82元.

當學生完成這道習題后，教師引導學生思考：在這個方程式中，“元”是什么？“次”是什么？學生回答該一元一次方程式的“元”是x，“次”為x的冪，即為1，于是它為一元一次方程式.

教師繼續(xù)引導學生思考：后來小紅又去水果店買東西，她這次買了5斤橙和3斤葡萄，總共花了25.4元，請問如何應用方程式來表達單價和總價的關(guān)系？

學生結(jié)合學過的知識來理解二元一次方程式的問題，學生發(fā)現(xiàn)，如果要用方程式來表示單價和總價的關(guān)系，那么就要涉及到橙、葡萄兩件事物，如果僅用一個未知元來表達，就不能列出方程式. 學生結(jié)合新的知識與舊的知識，理解了一元一次方程式就是方程式中有1個未知元，未知元的冪為1，那么二元一次方程式，就是方程式中有2個未知元，未知元的冪為1. 它們的共同特征之一，就是它們都是方程式，具有方程式的特征；共同特征之二，就是它們的冪都只有一次. 它們的不同特征是方程中包含的“元”的個數(shù)不同，且一元一次方程式可直接求解，二元一次方程式不能直接求解，學生必須掌握其他的已知條件，才能求出二元一次方程式的解.

學生學習過一些舊知識，對舊知識的機理有一定程度的理解. 部分新知識與舊知識之間有聯(lián)系，它們的知識框架有相同之處. 如果教師能夠引導學生結(jié)合舊知識的框架來理解新知識的框架，學生就能從知識框架的角度理解新知識的機理. 教師應用遷移的教學方法引導學生理解知識，實際上是應用縱向?qū)Ρ戎R的方法，幫助學生建立知識概念，當學生應用遷移的方式理解了新知識與舊知識的差異時，就能初步建立新知識的框架.

引導學生在探索中理解知識

當學生理解了概念的框架以后，需要繼續(xù)深入地理解知識. 學生只有理解了概念每一句指代的性質(zhì)意義，才能真正理解概念的意思，在應用概念的時候才不會犯下錯誤. 教師在教學中可以為學生布置典型的習題，引導學生從橫向、縱向?qū)Ρ葋砝斫飧拍? 教師引導學生橫向、縱向?qū)Ρ鹊倪^程，就是引導學生探索知識的過程，學生在對比中，可以全方位地了解新知識的特點，這一特點就是新知識概念區(qū)分于舊知識概念的地方.

以教師引導學生學習二元一次方程，深入理解二元一次方程的特點為例，教師可引導學生思考以下習題：請分析以下的算式哪些是二元一次方程：

學生經(jīng)過思考，首先排除掉（4）和（6），教師引導學生思考為什么這兩個不是呢？學生表示（4）中雖然出現(xiàn)了x，y兩個未知元，但y的次數(shù)是2，它屬于二元二次方程式. （6）是一元一次方程式. 關(guān)于（3）是不是二元一次方程式，很多學生犯了難，教師引導學生再次閱讀數(shù)學概念，并引導學生思考整式的次數(shù)是如何決定的. 學生經(jīng)過思考，發(fā)現(xiàn)（3）的階次是兩次，它不是一次方程式，這就如同ax·x或ax·y的階次都不是一次一般. 學生排除了（3）后，有學生指出，如果排除掉（3），那么（2）也必須排除，因為如果將（2）去分母，整合成方程標準式后，它為xy+1=-7y，即xy+7y+1=0，它的階次也為2. 教師引導學生結(jié)合這一題開始思考，二元一次方程式是什么？請用多種方法描述出來. 學生結(jié)合這一道題與教師的提示，開始思考二元一次方程式的標準表達式、性質(zhì)、表格的表示方法、坐標圖像的表示方法等.

當學生理解了新知識的框架以后，可能對概念還不太熟悉，應用概念知識時可能存在一些問題. 教師可以為學生布置數(shù)道習題，引導學生一一探討數(shù)學概念每一句描述的意思，讓學生從橫向?qū)Ρ鹊慕嵌壤斫庵R概念. 這樣能讓學生對比微觀案例來理解宏觀概念的意思，了解每一句宏觀概念描述的意義，并理解概念描述的每一句話之間的內(nèi)在關(guān)系. 這一教學過程是教師幫助學生填補新框架知識內(nèi)容不足的過程.

引導學生在生活中理解知識

當學生從橫向與縱向兩個角度理解了知識框架，找尋出知識框架的雛型以后，教師可為學生布置典型的習題，讓學生在應用中進一步理解知識.

現(xiàn)以教師引導學生思考以下習題為例：

甲車、乙車在周長為400米的環(huán)形跑道上移動，如果同時、同地、反向出發(fā)，兩車經(jīng)過80秒相遇. 已知乙車的速度是甲車速度的，求甲車、乙車的速度.

在這一次的學習中，學生發(fā)現(xiàn)了：

第一，在解決一個數(shù)學問題時，如果存在兩個未知量，那么可用設x和y元的方法列方程，應用這種方法可讓數(shù)學問題變得更簡單.

第二，應用二元一次方程方法的要求，就是科學地設元及根據(jù)已知條件列出等量關(guān)系.

第三，在考慮問題時，可以應用多種方法來解決問題，從中找到最佳的解決方案，學生學習的知識越多，就意味著學生可以采取的數(shù)學方案越多.

當學生獲得了知識框架以后，教師要引導學生在實踐中思考問題：

第一，教師要引導學生在實踐過程中思考知識概念的應用方法，從應用的角度更深入地理解知識；

第二，引導學生對比用舊知識解決問題和用新知識解決問題存在的差異，讓學生再次從對比中理解新知識與舊知識的關(guān)聯(lián)和差異，使學生能整合出較為完善的數(shù)學知識體系.

教師理解性教學分為三個步驟：

第一，引導學生遷移，從舊知識框架的角度理解新知識的框架；

第二，引導學生橫向?qū)Ρ龋寣W生深入理解新框架中每一條概念的意思；

第三，引導學生應用新知識框架，讓學生從實踐的角度再次橫向及縱向?qū)Ρ龋铣鲚^為完善的知識結(jié)構(gòu).endprint