變換思維角度:解決問題的有效策略
王文清

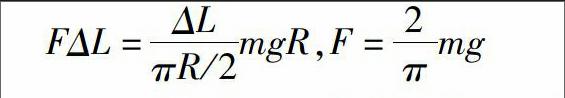

【內容摘要】新一輪課程改革對學生思維能力的培養提出來很高要求。如何結合物理學科培養學生的科學思維是需深入研究的問題。本文從日常教學案例著手,嘗試引導學生從轉變研究方向、靜態動態轉化、合理建立坐標、巧妙應用對稱等方面,變換思維角度,有效解決問題,培養學生發散思維和求異思維,從而提升學生的核心素養。
【關鍵詞】思維 策略 解決問題 核心素養 物理學科
即將啟動的以學生學科核心素養培養為目標的新一輪課程改革,對培養學生科學思維提出了很高要求。通過物理學科的學習要求學生“具有批判性思維的意識,能基于證據大膽質疑,從不同角度思考問題,追求科技創新”。當然,創新離不開求異思維和發散思維的培養,思維的過程就是創新能力和創新精神培養的過程。
一、 一個實驗引發的思考
在“超重與失重”的教學中,為了讓學生更好地理解超重與失重現象,筆者設計了這樣一個問題:一個人站在磅秤上,不借助其他工具,怎么樣才能使磅秤的讀數最大?幾乎所有的同學都采取了同樣的方法:人先蹲下,然后快速站起。站起時的加速度越大磅秤讀數的增加量也越大。然而,有一位同學卻采用了另一種方式:他先站直不動,接著快速下蹲,利用向下減速過程中的超重現象使磅秤的讀數增加。他這種不同常人的方式最終贏得了比賽。
這個同學解決問題的思維方式引起了筆者的思考:從不同的角度考慮同一個問題時,常常能發現一些易被忽視的東西,而其中包含了解決問題最重要的要素;鼓勵學生從不同的思維的角度來研究同一個問題,不僅對學生解題能力的培養有好處,更重要的是學生在問題研究中增強了創新意識,獲得了創新精神。
二、 應用變換思維角度解決問題的實例分析
在平時的教學中,筆者總是有目的地創造機會,讓學生展示他們在研究問題中表現出的創新能力和創新精神。下面是應用變換思維角度的策略來解決問題的一些實例分析。
1.轉變研究方向,尋找問題突破
案例1:線上拴一小球,從水平位置A由靜止釋放。在小球從水平位置A運動到豎直位置B的過程中,當線與豎直方向的夾角θ為何值時小球的豎直分速度最大?常規的思路是,根據機械能守恒定律得:mglcosθ=12mν2所以,ν=2glcosθ。豎直方向的分速度νy=νsinθ=2glcosθsin2θ,當cosθsin2θ取最大值時,豎直方向的分速度νy有最大值。然而,求解cosθsin2θ的極值需要一定的數學技巧,問題陷入了困境。這時,啟發學生變換思維的角度,研究豎直方向的分速度變化的原因。經過分析發現:前半個過程,由于重力大于繩子拉力的豎直方向的分量即:mg>Tcosθ,所以豎直方向處于加速狀態,豎直方向的分速度νy不斷增大;后半個過程,繩子拉力的豎直方向的分量大于重力,Tcosθ>mg,所以豎直方向處于減速狀態,豎直方向的分速度νy不斷減小。當mg=Tcosθ時, νy有最大值。
解決這個問題的關鍵在于,當從豎直方向的分速度 的表達式直接分析陷入困境時,變換思維的角度,從受力分析著手研究豎直方向分速度 變化的原因,找到了解決問題的突破口。
2.靜態動態轉化,抓住問題要害
案例2:一質量為m的均勻鏈條,繞在一光滑的1/4圓柱上,用一水平拉力作用,處于平衡狀態。求:一水平拉力F的大小。這是一個關于物體平衡的問題。開始似乎很難找到解題的切入口。當變換思維的方法,從另一個角度分析時發現了解決問題的切入口。假設鏈條在拉力F的作用下向左緩慢地移動了很小的一段距離ΔL,則底部的鏈條將上升了ΔL。通過這樣模型變換后,把原來的靜態問題轉化成了一個動態問題。當鏈條在拉力F的作用下移動了很小的一段距離ΔL過程中,相當于整個鏈條其它部分沒動,圓柱體底部的鏈條上升了R。對整根鏈條應用能量守恒定律:
FΔL=ΔLπR/2mgR,F=2πmg
問題馬上找到了答案。由于根據系統能量守恒定律進行求解抓住了問題的要害,題目求解簡潔明快。當告訴學生上述方法是物理學中經典的思想——虛功原理時,他們感受到創造性學習的成功帶來的快樂。
3.合理建立坐標,簡化問題研究
案例3:從傾角為θ的斜坡頂端以初速度ν0水平拋出一小球,不計空氣阻力,若斜坡足夠長,則小球拋出后離開斜坡的最大距離H是( )。
(A)ν022g
(B) ν02sin2θ2g
(C)ν02sinθ2g
(D) ν02tanθsinθ2g
如果采用通常的坐標建立的方法,水平方向為X軸,豎直方向為Y軸,則計算不僅麻煩,還需要一定的技巧。
4.巧妙應用對稱,深化問題認識
案例3:所示為白熾燈L1(規格為“220V 100W”)和L2(規格為“220V 60W”)的伏安特性曲線,根據該伏安特性曲線可以確定將L1、L2兩燈串聯接在220V電源上時,兩燈消耗的實際實際功率分別為多少?
在這個問題中由于白熾燈是非線性元件,其伏安特性曲線不能用解析式來表示,所以無法用公式直接求解。這種情況下白熾燈的工作狀態如何確定?是問題解決的關鍵。這個問題的求解,有學生想到了逐步逼近的方法。因為串聯電路中電流強度相等,用一直尺與橫坐標平行畫出一系列直線,當L1與L2兩燈的電壓之和為220V時,直線與兩伏安特性曲線的交點即為問題的解。
變換思維的角度是解決問題的一種有效策略。在實際解決問題的過程中,當常規的思路陷入困境時,如果能及時地變換思維的角度,往往能產生意想不到的效果。更重要的是,尋找獨特的思維角度的過程,正是對學生創新能力和創新精神培養的過程,他們在創造性學習的過程中體會到成功帶來快樂的同時,更堅定了對科學探索持久的熱情,逐步形成了學生發展終身受用的核心素養。
【參考文獻】
[1] 教育部.普通高中物理課程標準(實驗)[M].北京:人民教育出版社,2014(7).
[2] 趙國慶.思維可視化[M]. 北京: 北京師范大學出版社,2016(7).
(作者單位:安徽省安慶第一中學)endprint

