“研學后教”理念下的中學數學單元教學的策略研究

谷新婷

[摘? 要] “研學后教”理念對初中數學課堂的優化有著很好的啟發意義，本文以“研學后教”理論為指導，立足于初中數學單元教學，指出教師在教學中應研究學生的學習規律，引導學生自編習題，且理性地對待學生的錯誤.

[關鍵詞] 研學后教;初中數學;教學策略

當前的初中數學課堂倡導充分發揮學生的自主性. 在此背景下筆者認為，將“研學后教”理念運用于初中數學的單元教學中，有助于課堂效率的提升.

“研學后教”理論與初中數學? ? 課堂

“研學后教”理論是新課程改革不斷推進和發展過程中的重要產物，該理論要求教師在教學中有效地定位“學”與“教”之間的關系，由此更新自己的師生觀和教學觀，并將該理論積極運用于教學，讓課堂教學更加匹配學生發展的實際需要.

以“研學后教”理論來建構初中數學課堂時，教師在教學之前要充分做好“研學”工作，即教師要深刻研究學生的知識基礎、學法特點，同時要立足于學生的視角來分析學習材料，設計各種學習活動，探求適合學生的學法指導思路. 另外，教師還要精心編寫學案，指導學生自主“研學”，并在合作探究中突破學習難點;在學生進行交流互動的過程中，教師要恰當地進行點撥和啟發，引領學生展開更進一步的探究，從而達到教學目標.

“研學后教”理論指導下的初中數學單元教學策略

單元教學是當前初中數學教學的主要形式，如何從“研學后教”的理論出發精心組織教學，由此提升效率呢？筆者認為，除了平時最常見的有機整合單元內容，將零散的知識連成知識網絡等方法而外，還可以在“研學后教”理念指導下從以下幾個方面著手.

1. 研究學生的學習規律，優化其思維品質

蘇霍姆林斯基指出：“在人們的內心深處，大家都渴望讓自己成為一個研究者、探索者和發現者. ”結合初中生的學習特點我們可以發現，很多學生喜歡對一些新鮮而奇怪的問題發起挑戰. 進行初中數學單元學習時，很多學生在思維過程中暴露出了這樣的問題：他們過分關注問題的最終結果，忽視探究過程本身. 為此，教師要引導學生積極而主動地研究學習規律，進而在自己的反思行為中發現存在的問題，并由此促進問題的解決. 問題往往可以讓學生將自己的認識推向更深的層次，我們可以引導學生進行自發提問：“為什么要如此研究？是否存在我們沒有考慮到的情況？還需要用什么方法來進行檢驗或求證嗎？”這些操作有助于學生反復思考自己的學習過程，進而將思維提升到更加開闊而深刻的程度.

例題？搖 2017年5月，勒索病毒席卷全球，這種病毒的傳播速度非常快. 假如一臺計算機被病毒感染，那么在兩輪感染后將會有81臺計算機被感染. 請結合數學知識分析一下，每輪感染中平均每臺計算機將感染多少臺計算機.

這個問題衍生于2017年的網絡關鍵詞“勒索病毒”，以此為情境來引導學生探索，很容易激起學生的興趣. 教師將這個問題提供給學生，讓他們先自行研究，同時提醒學生不能只關注答案是什么，關鍵是要弄清楚思路探尋的過程.

以下是學生在交流過程中給出的答案：假設每一輪一臺計算機將感染x臺計算機，結合題意可得方程1+x+（1+x）x=81. 這是一個學生都比較熟悉的一元二次方程，但如果僅止于將答案解出，這個問題便沒有多少價值，那怎樣才能引導學生更加深入地展開分析與思考呢？筆者認為，應該引導學生先進行觀察，并嘗試對方程進行變形處理，即提取公因式（x+1）后，方程變成（1+x）²=81，在此基礎上，教師繼續提出問題：如果經過三輪感染，那一共有多少臺計算機被感染？請用含有x的表達式表示. 如果經過n輪呢？

學生展開思路，寫出計算式（1+x）²+x（1+x）²，并通過化簡指出第三輪被感染計算機的臺數為（1+x）³，在此基礎上，學生也能形成結論：經過n輪，被感染計算機的總臺數應該為（1+x）ⁿ. 當學生自認為問題已經完全解決時，筆者再拋出一個新的問題：“現實情形下，往往不止一臺計算機被感染，原題中‘假如一臺計算機被病毒感染這一條件變成‘假如2臺計算機被病毒感染，那問題又該如何處理呢？”學生經過分析，形成了結論：三輪之后被感染計算機的總臺數應該是2（1+x）³，經過n輪，被感染計算機的總臺數應該為2（1+x）ⁿ. 筆者再次提出問題：“原題中的條件變成‘假如n臺計算機被病毒感染，那么問題又該如何處理呢？”學生的思維再次被問題驅動，形成更加深刻的認識. 最后，筆者列舉出細胞分裂、銀行復利等問題，由此引導學生展開分析和比較，進而明確此類問題的相似之處.

以上例子是一元二次方程的應用，是整個“一元二次方程”單元的教學難點. 不少教師認為讓學生記住口訣“原量×（1±百分率）n=新量”，學生就能解決問題，結果，學生經常記錯公式或由于不理解公式而無從入手，根本不能達到教師的期望. 上述問題的設計隱含著整合單元知識的思想，能引導學生用同樣的思維方法解決同類問題;同時，這些問題都是在對學生思維特征進行充分研究的基礎上提出的，而學生在這些問題的啟發下展開更加深入的思考，他們的思維水平就會得到更深層次的提升和發展. 學生理解了上述問題的解決辦法，就不需要記憶任何公式，遇到類似問題，也能用同樣的方法解決.

2. 指導學生自編練習，激活他們自覺學習的意識

綜觀當前的數學教材我們發現，教材上所配習題相對較少，結合整個單元的知識設計的題目更少，而且梯度不強. 而如果由教師進行組題、編題，作業的統一性又太強，很難適應每個學生的學習需要. 在研究學生學情的時候我們還發現，學生在面對常態化的數學作業時，總提不起精神，這說明如果我們始終以現成習題的方式來組織學生進行課后作業，那效果將無法得到切實的保障. 怎樣改變這一情況呢？筆者認為，在新型的單元教學過程中，教師可以指導學生自行擬定習題，以此來檢查自己的學習水平. 學生在自編習題時，會把視線集中在自己的認知難點，在打磨習題的過程中必然會對相關知識或技能進行反復咀嚼，這一過程必然導致學生進一步熟悉有關知識和方法，而且這也會對學生創新思維的發展產生促進作用.

在學生自擬習題的時候，我們可以安排學生以學習小組為單位，相互出題與檢測，然后相互交流出題、做題的心得，相互促進，共同成長. 這樣可以讓學生的自主學習更具交互性，而且相互出題有助于學生變換思考問題的視角，可由此提升他們的認識. 比如學習“反比例函數”之后，學生在自編習題時，就編出了以下兩道習題.

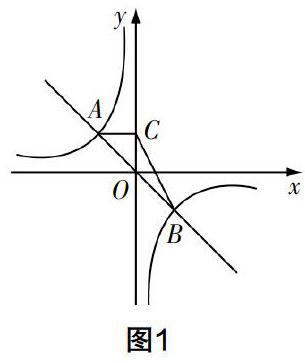
自編習題1？搖 函數y=-x和y=-4/x的圖像交于A，B兩點（如圖1），過點A作y軸的垂線AC，C為垂足，連接BC，求△BOC的面積.

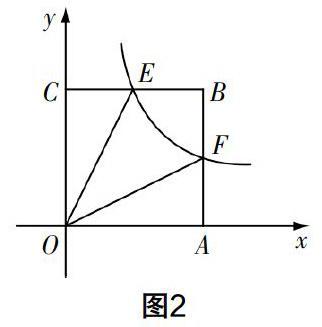
自編習題2？搖 已知雙曲線y=k/x（x>0）經過矩形OABC的邊AB和BC的中點F，E（如圖2），且四邊形BFOE的面積為2，請確定k的取值.

以上兩道題都涉及反比例函數知識，但考查的側重點不同，體現了題目的靈活多變性，避免了教師命題的單一性.

3. 理性對待錯誤，在糾錯中促進發展

“研學后教”理論倡導將學生推向知識探究的最前沿，這樣的操作必然導致學生在學習過程中發生很多錯誤. 面對這些錯誤，教師一方面不能過分苛責學生，另一方面也不能不管不顧. 教師要指導學生理性面對這些錯誤，合理而正確地展開分析和探索，讓學生在錯誤糾正的過程中實現發展.

比如學生在研究用平方差公式進行因式分解時，遇到了這樣一個問題：分解因式x4-y4. 筆者在巡查的過程中發現，一部分學生的答案是（x²+y²）（x²-y²）. 面對學生的錯誤，筆者沒有立即評價，而是讓學生自行觀察和比較. 學生很快就發現了問題：因式分解要徹底，既然（x²-y²）還可以分解，就需要繼續分解. 在這個處理錯誤的過程中，教師切不可因學生暴露問題而生氣，當然，也不可急切地糾正錯誤，我們應該將主導權移交給學生，讓他們在進一步的觀察與思考中形成更加深刻的認識，這才是“研學后教”理念指導下的有效教學！

面對學生的錯誤，教師的耐心與寬容顯得非常重要，當然，學生自己的心態也很重要. “研學后教”的教學過程本身應該是一個知識探索的過程，學生只有不斷地進行假設、論證，他們的認識才會不斷深化，方法和技巧才會逐漸成熟.

當我們將“研學后教”理念與初中數學單元教學進行融合時，數學教師要加強學習和反思，同時要結合學生的反饋來總結經驗教訓. 只有這樣，我們才能在實踐中不斷地進步和提升，課堂才會更加精彩.