關注學生起點 落實有效教學

徐佳梅

[摘? 要] 著眼于學生認知與思維、已有方法與經驗、經歷等學習起點進行設計與教學，能更加充分地激發學生學習的自主性與學習探究的熱情，因此，教師在具體教學中應不時關注學生學習的起點，并善于在學生起點處進行各種有意義的設計與落實.

[關鍵詞] 起點;認知;思維;方法;經驗;經歷;有效教學

大多數教師在平時的教學中都會根據自己預先準備的教案設計按部就班地完成課堂教學，教學目標也尤其現實地僅僅圍繞預設目標，這種嚴重忽略學生主動性與創造性的機械化教學對學生數學思維的發展極為不利. 數學是思維的體操，在課堂教學中注重發展學生的數學思維能力，提升學生的數學素養，才是數學教學最應該關注的內容. 因此，教師在平時的課堂教學中不僅不能忽視學生這一學習主體，還應在具體的教學中將學生主體凸顯出來，以促進他們數學素養的全面發展. 下面，筆者用具體例題表達自己在數學教學中的一點體會.

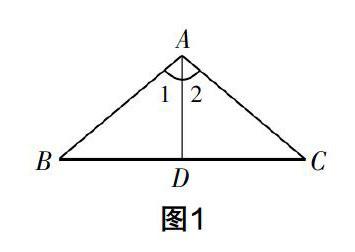
如圖1，在△ABC中，D為BC上一點，∠1=∠2，BD=CD，求證：AB=AC.

這是教材上的一個例題，筆者在此題的教學分析中比較關注學生的認知與思維起點，著眼于學生思維能力的提高，于是與學生一起進行了例題的解析.

1. 環節1：著眼于學生的認知與思維起點，激發學生的認知沖突與探求欲望

此階段的學生已經基本掌握了等腰三角形的判定與性質、全等三角形的判定與性質、逆命題、真假命題、圖形運動等知識與定理，學生懂得在AB=AC時，已知①∠1=∠2，②BD=CD，③AD⊥BC這三個條件中的任何一個就可以得到其他兩個，因此，筆者在此題的解析之初就著眼于學生已經掌握的等腰三角形知識拋出了下列問題：如果從①②③這三個條件中任意選出兩個作為題設，能夠得到AB=AC這一結論嗎？學生聯想逆命題的相關知識很快得出了三種情況，運用全等三角形的知識對其中兩種情況進行了證明. 不過，當①②兩條件作為題設時，原有圖形中已知等量關系的“SSA”結構卻無法判斷△ABD與△ACD全等，于是AB=AC這一結論也就無法說明了. 學生原有的知識與經驗對于這一問題的解決，明顯不夠，認知沖突自然產生的同時也將學生的求知欲望激發了出來：如果將②③作為已知條件，是否能得到AB=AC呢？筆者關注到了學生的疑問與思考，并及時提出了以下建議：大家可曾想過借助幾何畫板來判斷這一命題的真假呢？大家可以在圖形的運動中得到符合條件①②的△ABC，度量出AB和AC的長度后，再比較它們是否相等. 學生在教師的啟發之下很快投入到了積極而熱烈的討論與交流中：在∠MAN的平分線AE上任取一點D，過點D作直線BC與AM，AN分別交于B，C兩點，在交點B，C運動的過程中顯示BD，DC，AB，AC的度量值. 在點的運動中我們可以直觀觀察到：當BD≠DC時，AB≠AC;只有當BD=DC時，AB=AC. 由此可見，將①②作為題設確實能得到AB=AC這一結論. 具備一定質疑意識的學生此時不禁納悶：證明AB=AC又有什么用呢？順著學生的這一疑惑，后續例題解析的呈現也就水到渠成了.

筆者緊接著以學生的原有知識基礎對等腰三角形、全等三角形知識進行了復習，后續問題的解決也因為前面例題的討論獲得了很好的方法思考. 借助逆命題滲透問題形成的方法，也在關注學生認識與思維起點的教學中得以實現.

2. 環節2：著眼于學生已有方法這一起點，引導學生自主探究

此階段的學生已經掌握了利用全等三角形的性質、等腰三角形的判定來證明線段的一些方法，但因為之前的嘗試在此題的解決中不起作用，因此從AB=AC這一結論出發進行證明，是行不通的. 因此，學生轉換角度并著眼于條件開始嘗試. 學生面對∠1=∠2這一已知條件進行了以下思考：一個角關于角平分線呈軸對稱，可以將其翻折. 筆者關注到學生的這一思考并適時拋出問題：大家從角平分線上有沒有聯想到什么圖形呢？學生很快意識到圖形中有軸對稱圖形. 筆者順著學生的思維又拋出問題：大家可否從軸對稱圖形上聯想到什么操作運動？（翻折）怎樣翻折呢？通過翻折來說明AB=AC又該怎樣進行呢？筆者提出這些問題正是基于學生已有翻折這一實踐活動經驗而做出的考慮. 學生在問題的啟發下很快想到沿角平分線AD進行翻折的實踐操作，但解釋B點與C點重合時卻又產生了新的問題：已知條件中并沒有告訴我們∠ADB，∠ADC是否相等，B，C，D這三個點是否在同一條直線上也就無法說明了. 因此，借助角平分線的知識來解決此題也行不通.

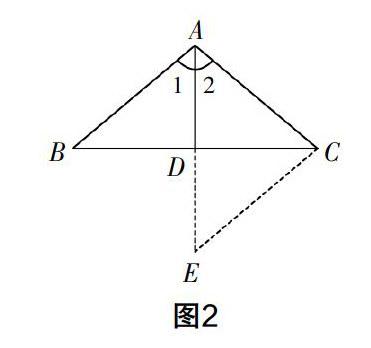
從前面一個條件出發來解決問題已經行不通，學生也就自然會再考慮第二個問題“BD=CD”. 借助角平分線知識雖然無法解決問題，但學生卻在這一階段的思考中獲得了圖形運動的思路，因此，筆者趕緊結合學生的這一認知，以及題中所給的中點這一條件啟發學生：大家看到點D為線段BC的中點這一條件了嗎？看到這一條件，大家可曾聯想到什么操作？（旋轉）學生的反應很快，但緊接著卻發現線段BD繞點D旋轉180°后點B和點C是能夠重合的，看上去跟AB，AC沒有聯系. 筆者關注到學生的思維發展后追問：點A能不能納入這一旋轉過程呢？學生的思考在教師的這一問題下變得更加深入：可以將△ABD繞點D旋轉180°得到△ECD，AB和AC就融進了同一個三角形中. 不僅如此，∠1與∠2本來是在兩個小三角形中的，現在都在△CAE中了（如圖2）. 根據等角對等邊可知AC=EC，因此AB=AC，問題獲解.

筆者在探究證明思路的解析過程中一直關注學生已經掌握的方法，并對學生的討論、交流進行了有效的引導和組織，解題思路也得到了很好的滲透：從待證結論或已知條件都可以進行一定的考慮，以證明幾何問題，如果行不通，應趕緊聯想已知相關知識與已有解題方法.

3. 環節3：著眼于學生已有經驗這一起點，引導學生自主反思

學生從失敗到成功的探究體驗中積累了問題形成、利用中點進行旋轉解決相關問題等經驗，筆者在學生已具備的抽象思維與概括能力的基礎上又拋出了以下問題：（1）嘗試運用旋轉這一操作，一般在出現什么樣的已知條件時可以運用呢？（2）大家以為在此題的解決中將圖形進行旋轉是為了什么呢？這些問題能促進學生自主反思與總結. 很快，學生的思維產生了碰撞，并進行了總結：圖形中出現對稱圖形時可以考慮旋轉這一操作，圖形重合的現象就會因此產生. 本題中的已知條件與待證結論在圖形的旋轉下得到了新的分布，待證結論和已知條件之間的距離因旋轉而得到了有效縮小，所以促進了問題順利解決.

學生的總結將學生在具體經驗中進行抽象概括的水平充分展現了出來，結論以及知識發生的過程都在概括中得到了完美體現.

4. 環節4：著眼于學生已有經歷這一起點，設計反饋練習

學生的小結以及解題探究過程在筆者的心里留下了極為深刻的印象，因此，筆者在本課的教學結尾階段，結合學生的認知狀態，進行了以下課堂反饋練習設計.

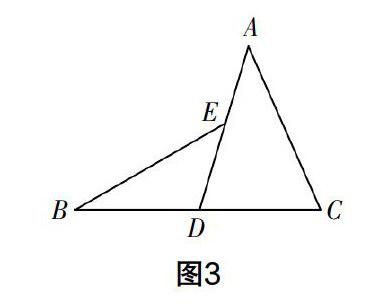
練習1 如圖3，已知∠BED=∠DAC，BD=CD，求證：BE=AC.

練習2 如圖4，在△ABC中，BD=CD，BF與AC，AD分別交于點F和點E，且AF=EF，求證：BE=AC.

練習3 如圖5，在△ABC中，∠BAD=∠DAC，BM=CM，過點M作AD的平行線與AB交于點E，與CA的延長線交于點F，求證：BE=CF.

已知一邊的中點，并能通過圖形的旋轉求證結論是這三個練習題共同的特征. 實際上，這是基于本課例題所做的變式. 學生在不同程度的變式中進行循序漸進的思考，學習參與的“廣度”與“深度”都得到了很好的保障，學生在不同程度的思考、探究與練習中對本課中所涉及的添線方法形成了牢固的掌握，認知與思維能力也在不同程度的思考中得到了有意義的鍛煉.

事實上，教師在具體教學中能夠不時關注學生的學習起點，并善于在學生起點處進行各種有意義的設計與落實，學生學習的自主性以及學習的熱情、探究新知的欲望，必能得到極其充分的激發，并最終實現思維能力的提升.