在小學相遇問題中培養學生的抽象思維能力

江蘇省江陰市南閘中心小學 居新霞

在小學數學教學中，教師必須一邊引導學生學習知識，一邊培養學生的抽象思維水平。小學生只有具備了抽象思維的能力，才能夠理解每個數學問題背后的核心本質。然后教師要如何培養學生的抽象思維能力呢？這是一些數學教師的困惑。現應用小學數學相遇問題的教學為例，說明培養學生抽象思維能力的方法。

一、引導學生提煉具象文本中的抽象信息

小學生的思維能力特點是具象化思維能力較強，他們容易沉浸在具象化的情境中、具象化的案例中，而不能從抽象的角度來理解具象化問題背后的本質。教師如果要培養學生的抽象思維能力，就要引導學生把抽象的本質與具象化的情境剝離開來，能用抽象思維來思考問題。

比如以教師引導學生思考以下的問題為例：快車和慢車同時從相距357千米的兩地出發，相向而行，經過3小時后快車與慢車相遇，快車的速度是95千米/時，則慢車的速度是多少？很多學生看到這個問題之后，把探索的信息放在快車是什么、慢車是什么？然后他們能夠不斷地發散聯想，把學習時間和精力投入到還原具象化的情境中。為了幫助學生建立抽象思維，教師要引導學生分析：第一，在文本中具有數量關系的事物是什么？第二，在文本中影響數量關系的關鍵詞是什么。經過教師的引導，學生會發現具有數量關系的事物是快車和慢車的行駛時間、快車和慢車的行駛速度、快車和慢車的行駛距離。影響數量關系的關鍵詞是兩地出發、相距、相遇、相向而行。文本中其他的信息與數量關系無關，于是不用花費精力思考。

教師在引導學生學習數學知識時，要引導學生學會抽取抽象的數量信息，這是學生學會應用抽象的視角分析數學問題的基礎。

二、引導學生分析具象圖形中的抽象關系

小學生的抽象思維能力還比較弱，他們不能在提取了文本中的抽象信息后，直接建立數學關系。為了讓學生能夠從具象化的數學問題抽取抽象化的數學關系，教師要引導學生學會根據抽象信息來繪制數學圖像，然后從數學圖像中提取抽象的數量關系。

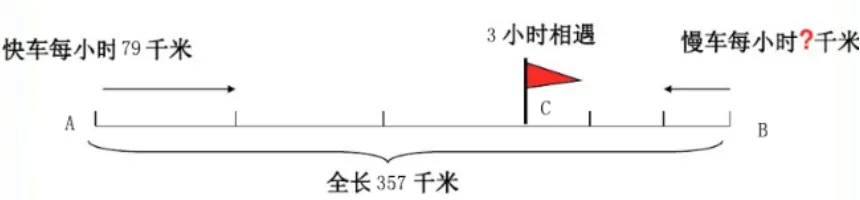
比如，當學生提取了文本中的數量關系以后，教師要引導學生畫標準的、規范的線段圖。教師可讓學生了解，現在快車和慢車相距是540千米，可以應用一條直線來描述這段距離；快車的起點設為A，慢車的起點設為B；根據文本的信息，快車和慢車都走了三個小時并相遇，那么現設相遇的地點為小旗所插之處，也可設為C；C的左側是快車行駛的距離、右側是慢車行駛，然后以快車和慢車相遇的時間，繪制單位時間的刻度，標注單位時間中快車及慢車的行駛速度。以上圖形中，如已有數量信息，則標注數量信息，如無數量信息，則設元為x。小學生通過觀看這樣的圖形，則立即理解了數學問題的數量關系：全長=快車行駛的距離+慢車行駛的距離，快車行駛的距離為時間×速度，慢車行駛的距離為時間×速度。根據數量關系可列方程，建立等量關系為357=3×79+3x，357=237+3x，3x=120，x=40。通過這一次的學習，學生意識到了當遇到相遇問題，不能建立數量關系時，可以把抽取到的數量關系繪制到圖形上，結合圖形來分析數量關系。

小學生的抽象思維能力不足，有時他們很難從抽象的層面來思考抽象的信息，為了幫助學生思維，教師在教學中要培養學生的數形思想。教師要引導學生學會把抽象的數量信息繪制在圖形上，然后結合圖形的信息來發現抽象的數學關系。通過這樣的訓練，學生會了解當抽象思維能力不足時，要如何應用具象化的圖形來分析抽象的數學關系，然后建立抽象的數學關系公式。

三、引導學生理解具體案例中的抽象規律

當學生學會了分析數學文本中的抽象信息，能夠建立抽象數學關系以后，教師要引導學生發現數學案例中的規律，然后根據具象化的案例中呈現出來的規律來歸納總結抽象的問題規律，這些規律可以成為學生解決這類問題的理論指導。

比如教師可引導學生分析以下的習題：小明和小華騎著電動車從相距190千米的兩地出發，相向而行。小明的行駛速度是36千米/時，小華的速度是40千米/時，兩人在幾小時后能相遇？教師可引導學生結合剛才學習的結果提取文本中的數學信息，通過繪制線段圖建立數學關系。學生經過思考，完成以上的步驟，得到方程：36x+40x=190，76x=190，x=2.5。當學生完成了學習以后，教師引導學生思考。剛才以上所有的問題探討的都是什么問題？學生經過思考，認為可以把問題歸納為相遇問題。教師引導學生思考，相遇問題涉及的數量關系是什么？學生表示涉及的數量關系為總距離、總速度、總時間；甲走過（或行駛）的距離、甲的速度、甲用的時間；乙走過（或行駛）的距離、甲的速度、甲用的時間。教師引導學生思考，結合以上的案例，可以建立哪些等量關系公式？學生經過思考，得到以下的公式：總距離=總速度×總時間；總距離=甲走過（或行駛）的距離+乙走過（或行駛）的距離；總距離=甲的速度×甲用的時間+乙的速度×乙用的時間；總距離=（甲的速度+乙的速度）×甲、乙相遇用的時間。當學生從具象的案例中抽取了這樣的數學公式以后，學生突然有所悟。學生意識到以后再遇到相遇問題時，可以直接套用這套規律來分析文本，建立數量關系；只要深入理解這套規律，他們甚至可以省去繪制線段圖的時間。

教師在教學中，要引導學生學會在具象化的案例中，抽取抽象化的數學規律。教師要引導學生發現具象案例中的共通點，在共通點中找規律。教師要讓學生意識到，學習數學知識時，不能只是掌握解決具象化數學案例的技巧，學生必須抽取解決某一類數學問題的規律，形成解決這一類數學問題的數學理論指導。只要學生長期受到這樣的訓練，他們就能夠從具象化的案例中抽取抽象化的理論。

總之，教師在教學中要引導學生學會抽取文本中的抽象化的數量信息、從數學圖形中分析抽象化的數量關系、在具象化的案例中抽取抽象化的規律。只要學生長期受到這樣的訓練，就能夠逐漸把具象化的情境與抽象化的本質剝離出來，然后學會從抽象化的角度思考問題。