用數學史促進學生數學核心素養的主動建構*

☉江蘇無錫市太湖格致中學 陳 鋒

☉江蘇無錫市東絳實驗學校 薛 鶯

一、問題的提出

隨著數學教學回歸本色，將數學史融入教學已悄然成為課堂一道靚麗的風景線，在數學教學中利用數學史將數學知識、方法、文化融為一體，不僅可以提升數學教學的有效性和趣味性，熏陶中國優秀傳統文化，提升數學文化素養，而且可以幫助學生提高在新情景下對知識的理解以及遷移到不同情境中去的能力，從而達到檢測學生思維的廣度和深度以及進一步學習的潛能.但是如果僅僅是把數學史當作數學相關歷史的簡單介紹，是遠遠不夠的，因為這樣做無法有效提升學生的學習能力.那么，怎樣才能更好地在數學教學中發揮數學史的功用呢？筆者以為，可以采用數學史更多元化地融入數學課堂教學，進而讓學生在數學學習的認知、思維和境界上都有所提升.現結合筆者的課堂教學實踐，來談一談自己在數學課堂教學中的一些做法，供各位教師參考.

二、數學課堂教學展示及效能分析

1.通過歷史成因揭示例題本質，掌握基礎知識，完善學生數學認知.

很多時候，學生在學習數學時，往往會產生這樣的想法：“學這個東西到底有什么用啊？”學生一旦有了這樣的想法但得不到解答時，就會覺得我們學習數學只是為了學而學，并無實際意義.于是，他們就會產生消極感甚至排斥感.要消除類似想法，可以借助數學史，依史說數學，解決學生的迷惑，并在解惑的基礎上進一步提升學生對所學知識的理解與掌握.

（1）例題展示：.

我國南宋數學家楊輝用三角形解釋二項和的乘方規律，稱之為“楊輝三角”.這個三角形給出了（a+b）n（n=1、2、3、…）的展開式的系數規律（按a的次數由大到小的順序）.請依據上述規律，寫出的展開式中含x2014項的系數：______.

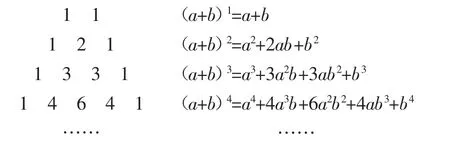
圖1

（2）教學流程.

在學生觀察、思考例題的基礎上，教師通過“你知道楊輝三角嗎”來激發學生的求知欲和學習興趣，接下來教師介紹楊輝三角產生的歷史，教師通過問題“你知道楊輝三角與二項和展開式的系數之間有怎樣的關系嗎”引導學生思考的方向和觀察的角度.由此，學生憑借對楊輝三角這一數學史的了解，發現楊輝三角就是展開式的系數的規律，進而順利完成問題的解答.最后教師對楊輝三角的數學史的知識進行拓展，讓學生了解楊輝三角是開方做法的本源.

（3）效能分析.

在這一例題的教學中，教師通過介紹楊輝三角這段數學史，首先，回答了學生“為什么會產生楊輝三角”的疑惑，讓學生感受楊輝三角具有言簡意賅、準確直白的特點，進而體會數學學習與古代優秀文化成果的聯系，再一次深刻感受民族文化的作用，產生學習的快感.其次，對二項和的乘方展開式形成整體認知：一方面通過史料的例子，學生可以很容易觀察到二項和的乘方展開式的系數與楊輝三角的關系，學生的學習變得直觀、明了，易于理解，而問題的解決也變得順理成章，水到渠成；另一方面，可以培養學生的“數感”，讓學生清晰地感知數學的形式美和簡潔美.因此，依傍數學史來講例題，既可以提升學生的認知，讓學生在學習過程中不再迷惘，并且能夠依靠數學史讓學生對所學的知識有進一步理解，使其對數學教學的內容有更好的掌握，使數學思維過程簡明、準確，從而更容易揭示數學對象的本質.

2.借助前人實踐挖掘例題內涵，掌握基本技能，促進學生的數學思維.

數學這門學科有其本身的特點，它不只是教授知識，更是在培養思維：教會學生思考，教會學生怎樣思考.在此時，往往可以借助數學史，讓學生看到前人是怎樣思考的，借助前人思考的方式解決問題，并且在前人的基礎上更進一步.

（1）例題展示.

我國古代《易經》一書中記載，遠古時期，人們通過在繩子上打結來記錄數量，即“結繩計數”，如圖2，一位母親在從右到左依次排列的繩子上打結，滿七進一，用來記錄孩子自出生后的天數.由圖可知，孩子自出生后的天數是________.

（2）教學流程.

學生看題、思考，教師直接讓學生回答后，追問：“你如何做的？你的根據是什么？”讓學生探究七進制進位方法的本質，接著通過“從圖中你又了解到用什么辦法來計數呢”“你了解結繩計數的典故嗎”等問題，引出對最早的記數方法——結繩計數和石子計數的介紹，引發學生對數學來源于生活實際的認同，最后教師用“遠古時期，為什么人們用滿七進一，而不用滿十進一”“你會用十進制來解決這個問題嗎”“如果是你，你更愿意用幾進制計數法”等一系列問題對例題進行引申，讓學生進一步感受和體驗進位制的“原形”.

（3）效能分析.

從這一案例可以看到，例題是以古代《易經》“結繩計數”為素材，按滿七進一計算自孩子出生后的天數，來獲得解決問題的途徑.教師首先通過介紹歷史典故，發現結繩計數法來源于生活實際，讓學生感受到前人發明的“結繩計數法”是一項光輝偉大的成就，讓學生理解數學文化，形成理性思維，同時能讓學生感受我國古代數學的成就，增強愛國情懷.這種“逐一計數”的方法體現了數學“一一對應”的思想和“化繁為簡”的轉化思想.其次，讓學生對計數法的進制進行探究，運用了類比的方法，讓學生在探究中自然感受到“結繩計數法”，方法雖好，卻有缺陷.在進一步的思考過程中，學生修正了前人的想法，彌補了結繩計數的缺陷，使方法更為完善，進而從數學的本源解決了這一問題.這正是借助前人的思維，來提升自己的思維.我們沿著前人的腳步前進，卻并不固步自封，而是能在前人的基礎上，更進一步.哪怕是一小步，也是一種超越前人的舉動.這樣不但可以訓練學生的思維，也能夠提升學生的自信心，而這兩者，都是數學課堂上應該達成的任務.

3.對照文史資料拓展例題外延，發展數學情態，提升學生數學境界.

歷史屬文，數學是理.文科有文藝、感性的一面，理科則以邏輯、抽象的面目出現.這兩者在課堂上如果能得到和諧統一，那么學生不但能學好數學，更能夠提升自身的境界，感受數學的魅力，也體驗到文學的絢麗.

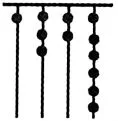
圖2

（1）例題展示.

我國古代有這樣一首古詩“枯木一根直立地上，高二丈周三尺，有葛藤自根纏繞而上，五周而達其頂，問葛藤之長幾何”.請求古詩中寓含的數學問題：葛藤的最短長度是_____尺.

（2）教學流程.

在學生閱讀古詩的基礎上，師生共同對古詩解讀，因一丈是十尺，因此得到題意是：一根枯木豎立在地面上，該枯木的高為20尺，枯木底面周長為3尺，有葛藤自枯木底部纏繞而上，繞五周后其末端恰好到枯木頂部.求葛藤的最短長度.進而讓學生明確題目的已知和問題，然后引導孩子根據題目的含意，把枯木看作一個圓柱體，畫出相應的圖畫（如圖3），接著教師追問：“如何解決求最短的長度這一問題？”引導學生首先把立體圖形轉化成平面圖形，圓柱體沿側面的母線展開是一個矩形，再在一個平面上求最短，利用直線最短和勾股定理即可求得.最后教師總結歸納在解決這個問題的過程中，用到了很多數學思想和方法.

（3）效能分析.

這一例題是一首古詩，把數學的問題撰寫成詩歌，是我國古代特別的一種數學形式，學生從中可以感受到詩歌與數學美并存其間，這是一種文藝美.而數學又將無數的歷史文學，化歸抽象成公式運算，這是數學的邏輯美.首先，近年來很多數學中考試題選自于中國古代數學名著，如《周髀算經》《九章算術》《孫子算經》等，其實不僅是中考試題，教材中也收集了中國古代數學問題，如“雞兔同籠”“百錢百雞”等，當然還有國外數學名題.其次，這些具有文化歷史背景的題目，根據已學過的基礎知識和思想方法再現探究過程，考查學生發現問題、提出問題、解決問題的能力，同時可以不斷地增強學生的創造力和數學學習的信念.再次，解答有歷史背景的題目，可以展現數學的文化價值，喚起學生的情感，如數學家及其著作的重要成果能夠喚起學生的民族自豪感和自主創新精神，經典歷史原題、名人名題能讓學生充分領略古代數學的思想精髓.寓教育于考試之中，挖掘數學文化內涵，即數學的精神、思想和方法.

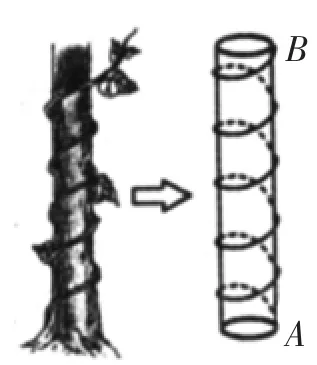
圖3

三、對數學史融入數學例題教學的思考

正如張奠宙教授所言：“學術形態向教育形態的轉化，實現從冰冷到火熱這一過程.”如果說數學從發明到呈現在教科書上，是“火熱的發明變成冰冷的美麗”，那么，將數學史融入數學課堂，把富有詩意的內容添入數學課堂中，則讓書上那冰冷的美麗又呈現出火熱的詩意來.在這樣的課堂上，學生不僅能學習數學，更能體驗到數學史帶來的美感，無形中也提升了學生的境界，開闊了學生的眼界.其實，學習數學的同時了解數學史，本應該如同學習語文名篇時掌握相關文學常識一樣理所當然.可是在很多時候，由于“實用主義”，我們往往有意無意地把這些原本應該了解的內容忽略掉了.反過來，在數學史介入數學課堂之后，我們也應該沿著前人的腳步或借用前人的眼光去觀察、學習、思考數學，并在前人的基礎上力圖有所升華.因此筆者認為教師要把握好以下幾點：

1.數學史的選擇要有“度”.

在數學例題教學中引用數學史時，數學史的選擇要能緊扣例題，聯系知識點，需要關注以下兩個“角度”.（1）適合學生實際.數學史的引用要適合學生的現有學習水平、潛能、興趣等因素.（2）把握例題的特點.不是所有例題都能引用數學史.這就要求教師對例題作深入鉆研，因為它是提升例題教學有效性的基礎.

2.數學史的引用要有“法”.

數學史的引用，離不開教師的引導，離不開例題作支撐，因此，教師引導的方式，教師是否適時、適度地引導，是數學史的引用成與敗的關鍵.因此要注意以下兩個“方法”.（1）要關注學生的差異性；盡可能滿足學生自主發展的需要，在教師的組織和必要的引導下，顯示學生自己的才華.（2）有些數學史不用探究，只要學生簡單了解、教師講解即可，而有些數學史為了今后能有效遷移，有必要進行延伸，讓學生自主探尋和發現.

3.數學史的呈現要有“方”.

在數學例題教學中引用數學史時，數學史的呈現需要關注以下幾個方面.（1）有些數學史學生都清楚，只要教師稍作提示即可.（2）有些數學史，學生已有所了解，需要教師必要的提示，再通過師生或生生之間的對話，互相啟發、互為補充才能完成.（3）有些比較生僻，教師可以借助信息技術輔助展示.

綜上可知，將數學史融入數學課堂，借助數學史進行數學教學，并不僅僅是一種“有趣的介紹”，也不是為了介入而介入，而是因為在實際運用中，數學史確實值得我們融入數學課堂之中.以史入數，憑史而學，史數相激，必能發出耀眼的火花.