注重習題教學 提升數學素養
——從六年級學業水平測試中的錯題談起

江蘇省啟東市紫薇小學 沈 燕

俗話說：“練拳不練功，到老一場空。”在小學數學教學中，教師只有引導學生加強習題練習，才能幫助學生深入理解、熟練運用和鞏固數學基礎知識，不斷提高分析問題和解決問題的能力。筆者以六年級學業水平測試中錯誤率較高的幾道習題為例，反思習題教學中存在的一些亟待改變的現象，試談對習題教學的幾點建議。

一、抓住概念本質，形成正確理解

【試題1】 有兩個三角形分別采用3厘米、4厘米、5厘米長的小木棒組成，以下關于這兩個三角形的哪一種說法是正確的（ ）

A.形狀不同，面積相等

B.形狀相同，面積不等

C.形狀相同，面積相等

本題考查學生對“三角形穩定性”的理解。蘇教版四年級下冊數學教材79頁對“三角形穩定性”給出了明確的解釋：“生活中許多物體上都有三角形的結構。這是由于三角形具有穩定性，也就是當一個三角形的三條邊的長度確定后，這個三角形的形狀和大小就不會發生變化。”此題是得分率最低的一道試題，可見大部分學生并未深入理解幾何意義上的“三角形穩定性”，或者說學生們感受到的“三角形不變形”和“利用對應長短相等的三根小棒圍成的多個三角形形狀都相同、大小都相等”建立不起聯系。

有些學生在學習“三角形穩定性”的內容時，往往存在著這樣的誤區：以“會不會拉得動” 為標準來判定多邊形是否具有穩定性，把操作活動注意點集中在了“會不會拉得動”的節點上。因此，在課堂上引導學生動手圍一個平行四邊形和一個三角形，然后拉一拉，當發現平行四邊形拉得動而三角形拉不動時，就可以判定三角形具有穩定性的特點。“是否拉得動”是學生形成錯誤邏輯的重要因素，可見，這樣的判斷標準是不科學的。

二、關注方法引領，感悟解題策略

【試題2】 兩個籃球隊隊員的身高和助跑摸高的成績如下表：

徐明 丁剛身高/cm 160 170成績/cm 250 265

人的身高在一定程度上影響著他的彈跳成績，直接用“250cm”和“265cm”來判斷哪一位隊員成績優秀不夠合理。請先計算出合適的數據，然后判斷到底誰的助跑彈跳能力更勝一籌？這道試題從六年級下冊數學書第75頁第10題中選取兩組數據提出問題，問題也就是書中的第1問。

【教材原題】學校男子籃球隊員的身高和助跑摸高的成績如下表：

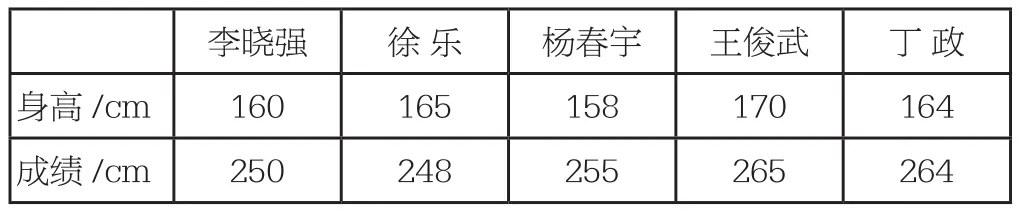
李曉強 徐 樂 楊春宇 王俊武 丁 政身高/cm 160 165 158 170 164成績/cm 250 248 255 265 264

（1）怎樣比較他們的成績更合理？先在小組討論，再算一算。

（2）一名專業籃球運動員身高188厘米，助跑摸高成績是351厘米。他助跑摸高的高度是身高的百分之幾？（用計算器計算）

教師教學用書上本題的旁注是：先用他們的助跑摸高成績除以他們的身高，然后再去比較所得商的大小，也就是比較這幾位同學助跑摸高成績與身高的百分比。雖然試題完全來源于教材，但大部分學生解題還是找不到方向。

那么，對于這道數學書上的習題，老師們是怎樣設計教學的呢？筆者在學業水平測試之后，曾和本校六年級老師談到這道習題。感覺初次看到這道習題會有一點發蒙，不過讀下去就知道怎么解答了，至于為什么，課堂上大家都沒有有意識地引導學生深入追究。習題中“小組討論”的要求也僅限于得出計算方法，由此還原的教學流程是：當老師提出第一問“怎樣比較他們的成績更合理？”學生有些茫然，然后就宣布討論，后來有些學生受第（2）問中問題的啟發，發現可以用“助跑摸高的高度是身高的百分之幾”來算。當這樣的想法得到肯定后，接下來的教學環節就是開始計算。教學過程缺失了學生的思考與討論，學生獲得的體驗只剩下——用計算器算完后，比比誰的值最大！

學生解答的高錯誤率提醒我們，習題教學的落點發生了偏差，習題的功能不能簡化為找到答案。教學是慢的藝術，是學生自己慢慢學會“走路”的過程。尋找解決實際問題的方法不妨慢一些，把思考還給學生。

問題怎么解決？要組織學生充分討論，在層層辨析中得出要用“助跑摸高成績與身高的百分比來比較”。討論時要有意識地引導學生深入思考：為什么要比成績是身高的百分之幾？怎樣想到“要用成績是身高的百分之幾”來比？教學要舍得花時間，組織學生探索解決實際問題的思考方法，從而感悟解決此類問題的解題策略。

因此，課堂上當學生根據第（2）問的提示，提出用“助跑摸高的高度是身高的百分之幾”來算的方法得到肯定后，他們是興奮的，但對為什么可以這樣比，理解上又是模糊的，這時適宜趁熱打鐵，走“知其所以然”的教學環節。

三、注重對比溝通，建立清晰認知

【試題3】 5公斤花生糖平均分裝在6個塑料袋子里，問每個袋子裝了多少花生糖（ ）

5公斤花生糖平均分裝在6個袋子里，根據這兩個條件，可以問每袋的具體數量有多少公斤，也可以問分率：每袋占總數的幾分之幾。題中的問題是“每個袋子裝了這些糖果的多少？”屬于部分量與總量之間的分率關系，應選A。

為區別是求分率還是求數量，常常能聽到教師介紹的一個“捷徑”，從題目的外部特征入手，問題中幾分之幾后有單位名稱，是求數量，用總量÷份數=每份數。幾分之幾后沒有單位名稱，是求分率，要想把單位“1”平均分成了幾分，部分量占單位“1”的幾分之幾。試題中問每個袋子裝了多少花生糖？用了“多少”而沒用“幾分之幾”來問。我們知道求具體數量也可以用“多少”這個詞來問，即“每個袋子裝了多少？”這兩種問法的“多少”后面都沒帶單位名稱。學生根據抓“外部特征”的思維方式，只看“多少”無法判斷到底是問分率還是具體數量，使得抓“幾分之幾后有無單位名稱”這一區別特征成為學生思考的障礙。因此，我們只有引領學生深入認識分數意義，才能讓他們在具體數量與分率的對比訓練中有所收獲。

教無定法，貴在得法。我們只有發揮習題的作用，厚實學生的學習過程，才能更好地幫助學生把握概念本質、掌握解決問題的方法，才能讓學生在習題訓練中提升核心素養。