運用有效策略，實現數學思維顯性化*
——以運用方程（組）解決實際問題為例

☉江蘇南京市江寧區周崗學校 徐 亮

☉江蘇南京市竹山中學 黃秀旺

在初中數學應用題教學中，學生往往因為生活閱歷有限，對應用題的背景和情境不熟，主觀認為應用題很難理解，從而影響了正常的數學思維，導致應用題無法解決.應用題解題的關鍵在于如何找出題中的數量關系，從而根據數量關系列出符合題意的方程（組）、不等式和函數關系式，這是學生對應用題畏懼心理的根源所在，而初中應用題題型的單一性，決定了解題中列式的難度并不大.筆者通過實踐，發現在用方程（組）解決實際問題的教學中，通過靈活運用以下幾種策略輔助分析，可為厘清題目中數量關系，將學生的數學思維顯性化，提供有效的幫助.

一、以關鍵詞為突破，實現數量關系的顯性化

小學階段的應用題是在文字題的基礎上結合具體的問題情境架構而成的，學生對解決文字題，把握關鍵詞的做法有著豐富的經驗積累.初中階段的應用題，題中經常會出現數量關系的關鍵字詞提示，教師只要通過合理的問題進行引導，就能讓學生很明了地厘清題中的數量關系，列方程（組）也就水到渠成.

例1（2017年徐州中考第24題）2017年4月9日上午8時，2017徐州國際馬拉松賽鳴槍開跑，一名34歲的男子帶著他的兩個孩子一同參加了比賽，下面是兩個孩子與記者的對話：

根據對話的內容，請你用方程的知識幫記者求出哥哥和妹妹的年齡.

分析：解決本題的關鍵就是對兩個數量關系式的提取，而其中的兩個關鍵詞就是解決此題的突破口，即妹妹所說的“和”，哥哥所說的“相加”，教師圍繞這兩個關鍵詞合理的設問引導，此題即可迎刃而解.

師：題中哪些關鍵字詞揭示了爸爸、哥哥、妹妹年齡之間的關系？

生：妹妹口中的“和”與哥哥口中的“相加”.

師：根據這兩個關鍵詞可以列出怎樣的數量關系式？

生：①妹妹的年齡＋哥哥的年齡＝16；

②兩年后妹妹年齡的3倍＋兩年后哥哥的年齡＝兩年后爸爸的年齡.

師：哪些量是已知的，哪些量是未知的？

生：已知爸爸今年的年齡34歲，兩年后是（34+2）＝36歲，妹妹和哥哥的年齡是未知的.

師：很好，這里有兩個未知量，那我們該如何求解呢？

生：因為有兩個未知量，所以我們可以設妹妹今年的年齡是x歲，哥哥今年的年齡是y歲，列出方程組求解.

……

學生解決方程類的應用題，從小學起就積累的良好的知識基礎.常見的題型及題型中的數量關系都是耳熟能詳的，教師在教學中只要引導學生把握題中的關鍵詞，諸如和、差、倍、分、增加、減少、擴大、縮小，等等.以關鍵詞作為解題突破的策略，結合基本題型的理解，排除問題情境中無關文字的干擾，應用題中各數量間的關系就可以自然地顯性呈現.數量關系式一目了然，轉化為方程求解也就順理成章.

二、以表格為手段，實現對應關系的顯性化

對于數量關系闡述不明顯的應用題，特別是營銷類問題、工程類問題等，學生如果不能很好地把握數量間的對應關系和變化特征，就會對題目中各數量之間關系的理解產生混亂，此時可以從基本的數量關系入手，引導學生借助表格，逐次呈現變化前和變化后的各個數量，讓對應關系顯性化，從而列出方程.

例2某商店的一種服裝，每件成本為50元.經市場調研，售價為60元時，可銷售800件；售價每提高5元，銷售量將減少100件.已知商店銷售這批服裝獲利12 000元，問這種服裝每件售價是多少元？

分析：一元二次方程應用中的常見問題，其基本的數量關系是：總利潤＝單件利潤×銷售數量，關鍵是通過對“每…每…”的理解，確定漲價后的單件利潤和降價后的數量.根據增加數量與漲價的對應關系，構造方程求解.

師：商品盈利問題中的基本數量關系是什么？

生：總利潤＝單件利潤×銷售數量.

師：銷售數量的變化受什么影響？影響的對應關系是怎樣的？

生：受漲價的影響，每漲5元，銷售量將減少100件.

師：若設售價為x元，則漲了多少元？銷售量又減少了多少件呢？

生：先求出漲的價錢為（x－60）元，再除以5，數量即

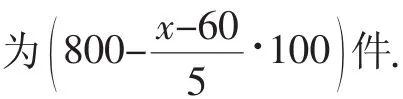
（這里的對應關系，有很多同學是不能清楚地表達的，教師可以引導學生借助表格，將數量與漲價之間的對應關系顯性化，從而清晰呈現數量與價錢之間的對應關系）

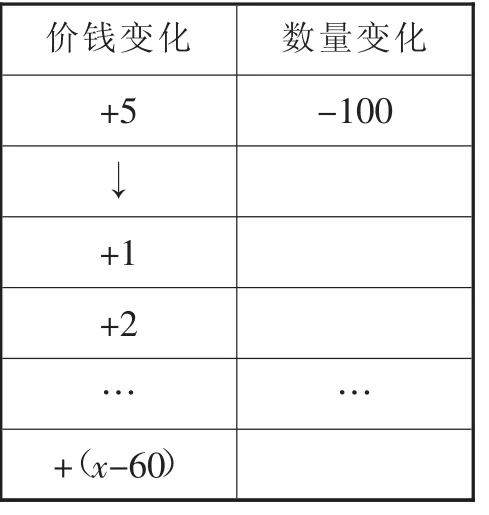
師：你能根據對應關系填寫以上表格嗎？

生：可以根據數量與價格間的對應關系填寫.

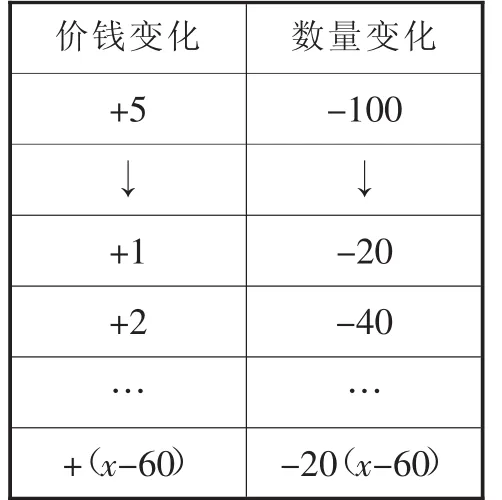
師：那根據銷售這批服裝獲利12000元，如何求解？

生：漲價后的單件利潤×漲價后的數量＝12000.

……

對于信息量大、數據繁多、對應關系復雜的應用題，借助表格手段，可以將題中數量關系和對應關系清晰地呈現.表格可以根據題型中的基本數量關系進行設計，也可以針對題中的主要對應關系設計，借助表格策略，實現復雜對應關系的顯性化，在學生解決工程問題、營銷問題等方面有著顯著的作用.

三、以圖形為輔助，實現抽象概括的顯性化

有些應用題文字敘述比較精練，數量關系比較抽象.受理解能力的局限，學生對于這一類題理解起來困難較大.如果一味地從字面去分析題意，用語言來表述數量關系，往往學生有“只可意會，不可言傳”的感受，教師在描述數量關系時，也會很蒼白，甚至會越講越復雜，越講越不易理解.在進行此類應用題教學時，以圖形作為輔助，可以將抽象的關系借助圖形直觀地顯現，便于學生理解.

例3某鐵路橋長1000m，現有一列火車從橋上通過，測得該火車從開始上橋到完全過橋共用了1min，整列火車完全在橋上的時間共40s.求火車的速度和長度.

分析：此題中有兩個問題：火車的速度和長度，雖然題中兩個“共”字清晰地揭示了兩個數量關系式，但對于“從開始上橋到完全過橋”和“整列火車完全在橋上”的理解，有不小的難度.

師：題中有哪些數量關系？

生：火車從開始上橋到完全過橋共用了1min，整列火車完全在橋上的時間共40s.可不知道如何列出數量關系式.

師：行程問題的中基本數量關系是什么？

生：路程＝速度×時間.

師：這對列出以上數量關系有什么提示？

生：路程1＝火車速度×1min；路程2＝火車速度×40s.好像不太好描述.

師：這里我們可以利用線段圖來幫助我們理解以上兩段描述的意思.

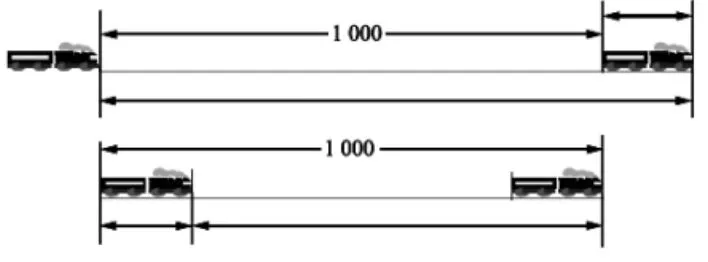
借助線段圖不難看出，火車用1分鐘（即60秒）的時間，行駛的路程實際上就是橋長與火車長之和；用40秒時間行駛的路程實際上就是橋長與火車長之差.

生：也就是說，橋長＋車長＝車速×60，橋長－車長＝車速×40，明白了.

……

這里采取的是線段圖策略.線段圖是小學解決行程問題中常用的策略之一，在行程類應用題中作用顯著，到了中學階段的學習后，學生更傾向于文字理解，忽視了線段圖的應用價值.線段圖的優勢，是將行程問題中的路程，用線段直觀地呈現出來，將諸如相向問題和追及問題中速度、時間的復雜關系，轉化成顯性的線段和、差之間的關系，教師需要引導學生回歸問題的本質，才能讓數學思維更自然地獲得發展.

例4某商場五月份的銷售額為300萬元，六月份的銷售額下降了10%，商場從七月份開始，改變了營銷策略，銷售額穩步上升，八月份的銷售額達到了326.7萬元.求七、八月份的平均增長率.

分析：這題中的增長率問題雖是平均增長率，但與平時訓練的又有所不同.涉及到三個月份的增長，其中六月份還是負增長，學生對這里的增長率關系的理解還是有一定困難的，可以借助框架圖，來對題中數量間進行抽象概括，直觀地顯現各月份之間的關系.

師：題中描述了幾個月份的銷售額情況？如何增長的？

生：六、七、八三個月份，其中六月份下降了10%，七、八月份都增長了，并且七、八月份增長率相同.

師：這三個月銷售額分別是在哪個月的基礎增長的？基礎銷售額都知道嗎？

生：六月在五月基礎上，七月在六月基礎上，八月在七月基礎上增長的；五月的銷售額是300萬元，六、七月份銷售額都不知道；八月份最終銷售額是326.7萬元.

師：那八月份的銷售額326.7萬元是如何計算出來的呢？

生：可以設七、八月份平均增長率為x，但缺少六月份的銷售額.

師：我們可能通過完成以下框架圖來解決六月份銷售額的問題.

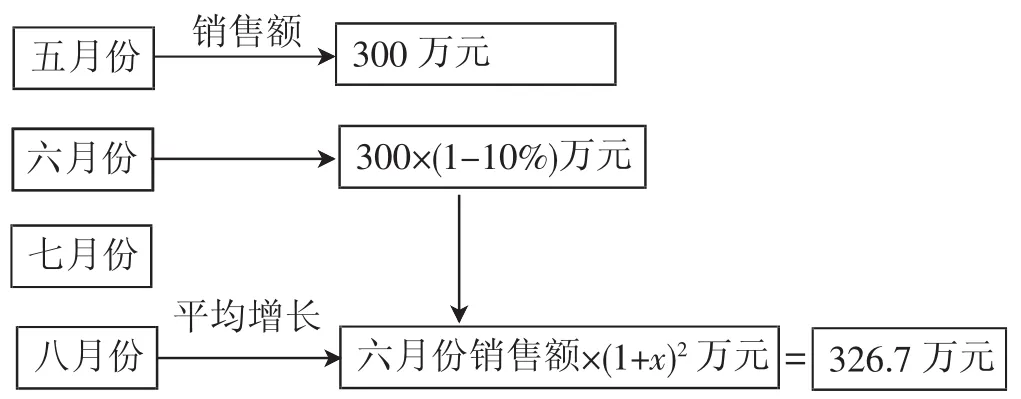
生：知道如何求解了.

……

框架圖是圍繞某一主題，用知識結構和框架的形式揭示數量間的關系，運用框架圖對復雜的數量關系進行歸類、分析、加工，有利于學生探尋問題的本質，從而實現抽象關系的顯性化，實現解題的目標.

用方程（組）解決應用題的策略還有很多，本文只例談了初中階段最常用的三種方法.在教學時應注意的是，不要刻意要求學生固定地選擇其中的某一種，而是要根據題目的特點，靈活地選用一種或綜合幾種，通過這些策略，讓學生體會到把數學思維顯性化的方法，真正提高分析問題和解決問題的能力，變“聞題色變”為“破題歡顏”，從而將感受“數學之用”提升到感悟“數學之美”.

參考文獻：

1.義務教育數學課程標準（2011年版）［S］.北京：北京師范大學出版社，2012.

2.王燕燕.初中數學思維顯性化的思考［J］.中學生數理化（教與學），2014（6）.

3.付志芳.初中數學應用題的教學策略及解題技巧［J］.西部素質教育，2016（6）.H