高中數學三角函數的教學策略研究
陳祖謙

[摘 要]三角函數作為高中數學課程中的重要板塊,其理論性和抽象性較強,學生比較難以理解.在高中數學三角函數的教學中,教師應引導學生熟背三角函數概念,靈活運用三角函數的公式和圖像,從而有效解決三角函數問題.
[關鍵詞]三角函數;高中數學;教學策略
[中圖分類號] G633.6 [文獻標識碼] A [文章編號] 1674-6058(2018)17-0015-01
三角函數也叫作“圓函數”,即角的函數,這種函數在研究學習三角形、建模周期現象和許多其他應用中是很重要的.除此之外,三角函數還是高中數學課程中的重要板塊.因此,教師應重視高中數學三角函數的教學,不斷優化三角函數的教學方法,提升三角函數教學的質量,從而讓學生有效掌握三角函數的相關知識及學習方法.
一、熟背三角函數概念
在教學高中數學三角函數時,教師首先要要求學生能熟背三角函數的概念,先讓學生背誦三角函數的基礎概念,在鍛煉學生自我概述三角函數概念的能力的同時,再讓學生進行理解性記憶,加深學生對三角函數概念的印象.
例如,在學習三角函數的概念時,教師可以設置一些問題提問學生,通過對問題的解答促進學生有效理解三角函數的概念,進而構建完整的三角函數概念體系,這樣不僅可讓學生深刻理解概念,還可以促進師生互動,提高學生的參與度和學習效率.
二、靈活應用三角函數公式
對于高中數學三角函數的公式,學生大多都能背誦下來,但是在實際應用中,學生卻不懂得去靈活應用,使得三角函數的學習加大難度.因此,教師在讓學生背熟公式的基礎上,應引導學生對公式進行推導,從而有效理解公式的本質,同時精選一些習題讓學生進行訓練,促進學生靈活應用公式.
例如,在銳角三角形ABC中,A、B、C的對邊是a、b、c,[ba] + [ab ]= 6cosC,則[tanCtanA+tanCtanB]=( ).
A.1 B.2 C.3 D.4
本題主要考查運用三角形的正弦定理和余弦定理求解三角函數值,屬于基本公式的綜合應用,這就需要學生在解題時學會靈活運用公式,進而有效解答問題.
三、掌握三角函數圖像的規律及作法
除了要求學生熟背三角函數的概念及學會靈活運用三角函數的公式外,教師還要結合三角函數的特點引導學生掌握三角函數圖像的規律及作法,從而讓學生理解三角函數的性質,促進學生數學思維的發展.
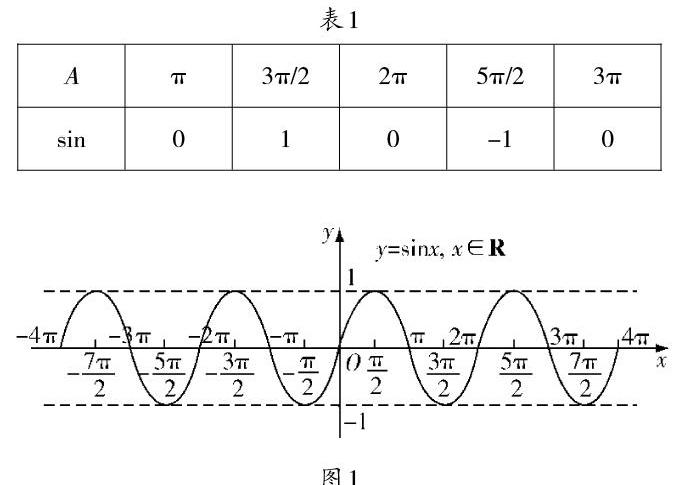
例如,對于三角函數中的正弦函數,教師可通過五點作圖法(如表1和圖1)引導學生學習,讓學生掌握正弦函數的圖像,并能根據相關圖像對正弦、余弦、正切等進行類比定義,進而找準值域,正確判斷周期等問題,使得學生可從圖像中全面地學習三角函數.
四、將三角函數問題與實際生活相結合
在學生解決三角函數問題時,教師應引導學生將三角函數問題與實際生活相結合,或者讓學生嘗試利用三角函數知識解決生活實際問題,只有這樣,學生才能有效掌握三角函數知識,提升解決三角函數問題的能力.
例如,在教學三角函數時,教師可拿一塊扇形鐵皮材料,告訴學生這塊鐵皮可以制作成一塊矩形,同時提問:“怎樣才能保證這塊矩形鐵皮的面積最大呢?”然后接著告訴學生:在生活中,一些工人師傅一般讓矩形的一邊為扇形的半徑,然后將其作為最大的內接矩形.此時,教師再次提問學生:“工人師傅是怎樣選擇矩形的四個點的?工人師傅都是采用我們現在所學的三角函數求出最大面積值,那么他們是怎樣利用三角函數計算的呢?
綜上所述,對于三角函數的教學,教師必須根據學生的學習特點,靈活地應用教學方法,進而保證學生的學習質量,并且經過實戰練習,保證學生確實學懂、學會,進而提高課堂教學的質量.
(特約編輯 安平)

